inzhenernaya_grafika / ИКГ Материалы / Заочное отделение / Заочники 1 сем / 2 Задание Д2 Плоские сечения / Начертательная геометрия.Теория

Начертательная геометрия - это наука позволяющая изображать пространственные образы на плоскости и решать графическим путем задачи с этими образами

Основоположник начертательной геометрии - Гаспар Монж.

Яковлев - читал первый курс начертательной геометрии в России в 1798г.

МЕТОДЫ ПРОЕЦИРОВАНИЯ

1-Центральное проецирование

Где: П - плоскость проекции;

S - центр проецирования (не лежащий на плоскости П);

A и B - точки в пространстве;

a,b - проекции точек на плоскости П;

Aa и Bb - проецирующие лучи.

Проекция точки - это точка пересечения проецирующего луча с плоскостью проекции.

Все проецирующие лучи проходят через одну точку S.

2-Параллельное проецирование

S - направление проецирования.

Все проецирующие лучи параллельны между собой и параллельны S.

Параллельное проецирование подразделяют на два вида:

- косоугольное – это такой вид проецирования, при котором проецирующие лучи составляют с плоскостью проекции угол отличный от прямого;

-ортогональное - это такой вид проецирования, при котором проецирующие лучи перпендикулярны к плоскости проекции.

МЕТОД МОНЖА

В основе этого метода положено ортогональное проецирование на две (три) взаимно перпендикулярные плоскости.

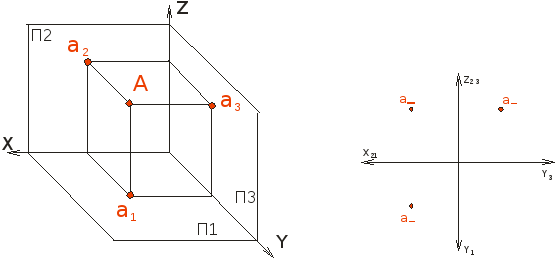
П1 - горизонтальная плоскость;

П2 - фронтальная плоскость;

П3 - профильная плоскость.

ОСНОВНЫЕ ИНВАРИАНТНЫЕ СВОЙСТВА

ПАРАЛЛЕЛЬНОГО ПРОЕЦИРОВАНИЯ

При проецировании на плоскость проекции геометрической фигуры в общем случае искажаются, причем характер искажения зависит от аппарата проецирования и положения проецируемой фигуры относительно плоскостей проекций.

Но между оригиналом и его проекцией существует определенная связь, т.е. Некоторые свойства оригинала сохраняются на его проекции, эти свойства называются инвариантными.

К основным инвариантным свойствам относятся:

1 - проекция точки есть точка;

2 - проекция прямой на плоскость есть прямая;

3 - если в пространстве точка принадлежит линии, то ее проекция принадлежит проекции этой линии;

4 - проекции взаимно параллельных прямых взаимно параллельны, а отношения отрезков таких прямых равно отношению их параллельных проекций;

5 - точка пересечения проекции пересекающихся прямых является проекцией точки пересечения этих прямых;

6 - плоская фигура параллельная плоскости проекции, проецируется на нее в конгруэнтную фигуру.

ПОВЕРХНОСТИ

В математике под поверхностью подразумевается непрерывное множество точек. В инженерной графике - поверхность рассматривается как совокупность всех последующих положений некоторых линий перемещающихся в пространстве по определенному закону.

Если рассматривать поверхность, как непрерывное, однопараметрическое множество линий, то линия определяется, как однопараметрическое множество точек. Следовательно, поверхностью называется непрерывное двупаранометрическое множество точек.

Образование поверхностей.

Рассматривая поверхность, как совокупность последовательных положений линии - “образующая”, перемещающаяся по определенному закону, по направляющим, мы получаем множество линий определяющих поверхность, называемые каркасом.

В число условий определителей поверхности входят геометрическая часть (точка, прямая, плоскость) и алгоритм формирования поверхностей.

Ф=(Г)+[A]

Классификация поверхностей.

- линейчатые поверхности;

- поверхности вращения;

- циклические поверхности;

- топографические поверхности.

Линейчатые поверхности

- называется поверхность, которая описывается, какой либо прямой (образующая). При ее движении в пространстве, по какому либо закону (направляющие).

Частный случай: Если направляющая - прямая, то поверхность плоскость.

Если точка лежит на линии принадлежащей поверхности, то она принадлежит всей поверхности.

Все образующие конуса пересекаются в одной точке, которая называется вершиной.

Если направляющей является ломаная линия, то получим частный случай конической и цилиндрической поверхности - пирамидальная и призматическая поверхность.

Поверхности вращения.

-Эти поверхности образованы вращением, какой либо линии (образующей) вокруг неподвижной оси.

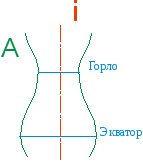
Определителями поверхности являются образующая (А) и ось вращения (i).

Окружности, по которым перемещаются точки образующей при ее вращении, называются - параллелями.

Параллель, полученная вращением точки с наибольшим радиусом, называется экватором.

Экватор определяет горизонтальный очерк поверхности. Параллель наименьшего радиуса называется горлом.

Сфера - образуется вращением окружности вокруг оси i проходящей через центр этой окружности.

Тор - образуется вращением окружности вокруг оси i не проходящей через ее центр. Если ось вращения проходит вне окружности, тор называют - открытым или кольцом. Если ось вращения лежит в одной плоскости с окружностью и при этом пересекает ее, то образуются закрытые торы.

ПЛОСКИЕ СЕЧЕНИЯ ПОВЕРХНОСТЕЙ

1. Пересечение многогранника плоскостью - в результате получается замкнутая ломаная линия. Точками излома являются точки пересечения ребер многогранника с секущей плоскостью. А звеньями лома являются линии пересечения граней с секущей плоскостью. Если секущая плоскость является проецирующей, то линия пересечения определяется сразу же, на той плоскости проекции относительно которой секущая плоскость параллельна.

2. Пересечение криволинейной поверхности плоскостью - в результате получается плоская кривая линия (для линейчатых она может распадаться на прямые). Фигуру сечения строят отдельными точками - начиная с опорных точек к которым относятся наивысшие и наинизшие, точки раздела видимости, крайние левая и правая, наиболее близкая и удаленная по отношению к наблюдателю; характерные точки - это большая и малая ось эллипса, вершина и основания гиперболы и параболы. Только после этого строятся промежуточные точки.

Пересечение плоскостью цилиндра

Р - под произвольным углом к основанию и оси вращения - эллипс,

М - параллельна основанию - окружность,

А -параллельна оси вращения - прямоугольник.

Пересечение плоскостью конуса

Р - параллельна оси вращения - гипербола,

М - параллельна образующей - парабола,

А - проходит через вершину - треугольник,

S - под произвольным углом к основанию и оси вращения - эллипс,

C - параллельна основанию - окружность.

Пересечение плоскостью сферы

В результате всегда получается окружность но на плоскости проекций она может выродится в линию или эллипс.