ekzamen (1)

Тема 1. Квантовые свойства света и волновые свойства вещества.

Световой поток, сила света, закон освещенности

Световой поток

Энергия излучения определяется количеством квантов, которые излучаются излучателем в пространство. Энергию излучения (лучистую энергию) измеряют в джоулях. Количество энергии, излучающейся в единицу времени называется потоком излучения или лучистым потоком.

где: Qе - энергия излучения. Измеряет в Лм

Сила света

Пространственную плотность светового потока, определяющуюся отношением светового потока к телесному углу с вершиной в точке размещения источника, в пределах которого равномерно распределен этот поток, называют силой света:

где: Ф — световой поток; ω — телесный угол Единицей силы света является кандела. 1 кд.

Освещенность Освещенность - это количество света или светового потока, падающего на единицу площади

поверхности. Она обозначается буквой Е и измеряется в люксах (лк).

Закон освещенности

Энергетическая светимость и испускательная способность тел, их взаимосвязь.

1

Закон Стефана-Больцмана.

1 и 2 законы Вина.

Формула Планка для теплового излучения.

Уравнение Эйнштейна для внешнего фотоэффекта.

2

Энергия, импульс, масса фотона.

Формула Комптона

Давление света при наклонном падении

давление света при наклонном падение : ρ= (1+ ρ)*сos2α

Длина волны де Бройля для классических и релятивистских частиц.

Длина волны де-Бройля для не релятивистской частицы массой m имеющей кинетич

Соотношения неопределенностей (5 соотношений).

Основы квантовой механики, физики атома и ядерной физики

Стационарное уравнение Шредингера.

Физический смысл волновой функции. Условие нормировки.

Собственные функции для частицы, движущейся в одномерной прямоугольной потенциальной яме. Вероятности нахождения частицы в различных областях ямы. Постулаты Бора.

Энергия электрона в атоме водорода (в эВ). Радиус орбиты электрона (через первый Боровский радиус).

Квантовые числа, их роль (таблица). Принцип Паули. Дефект массы. Энергия связи ядер.

Закон радиоактивного распада. Активность радиоактивного вещества.

Законы сохранения при ядерных реакциях (уметь применять в ядерных реакциях).

Статистическая физика и термодинамика

Первое начало термодинамики.

Энтропия (формула-определение). Второе начало термодинамики.

Распределение Больцмана. Барометрическая формула Распределение Максвелла (формула и график). Функция распределения Бозе – Эйнштейна.

Функция распределения Ферми – Дирака для электронов в полупроводнике.

Физика полупроводников.

Связь энергетической диаграммы с кристаллической структурой вещества. Температурная зависимость удельного сопротивления металлов. Температурная зависимость удельной электропроводности собственных полупроводников.

Закон действующих масс.

Температурная зависимость собственной концентрации. Внутренняя и внешняя контактная разность потенциалов в металлах. Высота потенциального барьера p-n перехода.

Ширина области пространственного заряда p-n перехода при равновесии и приложении внешнего напряжения..

Возникновение области пространственного заряда при контакте p- и n- полупроводников (теория).

Энергетическая диаграмма p-n перехода в равновесии, ее изменение при приложении внешнего электрического напряжения.

ВАХ p-n перехода (формула и график).

4

Тема 2. Основы квантовой механики, физики атома и ядерной физики.

1) Стационарное уравнение Шредингера.

( )

2) Физический смысл волновой функции. Условие нормировки.

Квадрат модуля волновой функции равен плотности вероятности нахождения частицы в данной точке в момент времени.

Условие нормировки

∫

3)Собственные функции для частицы, движущейся в одномерной прямоугольной потенциальной яме. Вероятность нахождения частицы в различных областях ямы.

Собственные функции для частицы, движущейся в одномерной прямоугольной потенциальной яме.

( ) √

Вероятность нахождения частицы в различных областях ямы.

∫

4) Постулаты Бора.

Первый постулат Бора: в атоме существуют стационарные (не изменяющиеся со временем) состояния, в которых он не излучает энергии.

Второй постулат Бора: В стационарном состоянии атома электроны движутся по стационарным орбитам, для которых выполняется квантовое соотношение:

, где n=1,2,3…

Третий постулат Бора: При переходе электрона с одной стационарной орбиты на другую излучается (поглощается) один фотон с энергией:

5

5)Энергия электрона в атоме водорода (в эВ). Радиус орбиты электрона (через первый Боровский радиус).

Энергия электрона в атоме водорода (в эВ):

Радиус орбиты электрона (через первый Боровский радиус):

6) Квантовые числа и их роль (таблица). Принцип Паули.

Квантовые числа и их роль (таблица).

Принцип Паули: в одном и том же атоме не может быть более одного электрона с одинаковым набором четырех квантовых числе n, l,ml и ms, т.е.

7) Дефект массы. Энергия связи ядер.

Дефект массы – разница между суммой масс всех нуклонов, содержащихся в ядре, и массой ядра.

,

6

Энергия связи ядра:

8) Радиоактивного распада. Активность радиоактивного вещества.

Закон радиоактивного распада

( )

Активность радиоактивного вещества –число ядер, распавшихся за единичный промежуток времени.

9)Законы сохранения при ядерных реакциях (уметь применять в ядерных реакциях).

Законы сохранения электрического заряда и числа нуклонов: суммарный электрический заряд и и полное число нуклонов вступающих во взаимодействие должно сохраняться в результате ядерных реакций.

Законы сохранения энергии и импульса: Законы сохранения энергии и импульса приводят к следующим соотношениям между импульсами и энергиями частиц до и после взаимодействия.

Закон сохранения момента количества движения: В ядерных реакциях сохраняется полный момент количества движения замкнутой системы

Где − полные моменты количества движения в начальном и конечном состояниях.

7

Тема 3. Статическая физика и термодинамика.

1.Первое начало термодинамики представляет собой закон сохранения энергии, один из всеобщих законов природы (наряду с законами сохранения импульса, заряда и симметрии):

Энергия неуничтожаема и несотворяема; она может только переходить из одной формы в другую в эквивалентных соотношениях.

Первое начало термодинамики представляет собой постулат – оно не может быть доказано логическим путем или выведено из каких-либо более общих положений. Истинность этого постулата подтверждается тем, что ни одно из его следствий не находится в противоречии с опытом. Приведем еще некоторые формулировки первого начала термодинамики:

Полная энергия изолированной системы постоянна;

Невозможен вечный двигатель первого рода (двигатель, совершающий работу без затраты энергии).

Первое начало термодинамики устанавливает соотношение между теплотой Q, работой А и изменением внутренней энергии системы ΔU:

Изменение внутренней энергии системы равно количеству сообщенной системе теплоты минус количество работы, совершенной системой против внешних сил.

(I.1)

(I.2)

Уравнение (I.1) является математической записью 1-го начала термодинамики для конечного, уравнение (I.2) – для бесконечно малого изменения состояния системы.

Внутренняя энергия является функцией состояния; это означает, что изменение внутренней энергии ΔU не зависит от пути перехода системы из состояния 1 в состояние 2 и равно разности величин внутренней энергии U2 и U1 в этих состояниях:

(I.3)

Следует отметить, что определить абсолютное значение внутренней энергии системы невозможно; термодинамику интересует лишь изменение внутренней энергии в ходе какого-либо процесса.

Рассмотрим приложение первого начала термодинамики для определения работы, совершаемой системой при различных термодинамических процессах (мы будем рассматривать простейший случай – работу расширения идеального газа).

Изохорный процесс (V = const; ΔV = 0).

Поскольку работа расширения равна произведению давления и изменения объема, для изохорного процесса получаем:

(I.1)

(I.4)

(I.5)

Изотермический процесс (Т = const).

Из уравнения состояния одного моля идеального газа получаем:

8

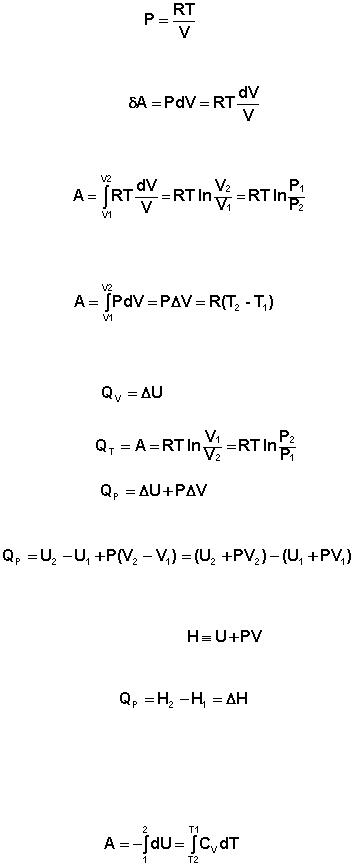
(I.6)

Отсюда:

(I.7)

Проинтегрировав выражение (I.6) от V1 до V2, получим

(I.8)

Изобарный процесс (Р = const).

(I.9)

Подставляя полученные выражения для работы различных процессов в уравнение (I.1), для тепловых эффектов этих процессов получим:

(I.10)

(I.11)

(I.12)

В уравнении (I.12) сгруппируем переменные с одинаковыми индексами. Получаем:

(I.13)

Введем новую функцию состояния системы – энтальпию H, тождественно равную сумме внутренней энергии и произведения давления на объем:

Тогда выражение (I.13) преобразуется к следующему виду:

(I.14)

Т.о., тепловой эффект изобарного процесса равен изменению энтальпии системы.

Адиабатический процесс (Q = 0).

При адиабатическом процессе работа расширения совершается за счѐт уменьшения внутренней энергии газа:

(I.15)

В случае если Cv не зависит от температуры (что справедливо для многих реальных газов), работа, произведѐнная газом при его адиабатическом расширении, прямо пропорциональна разности температур:

9

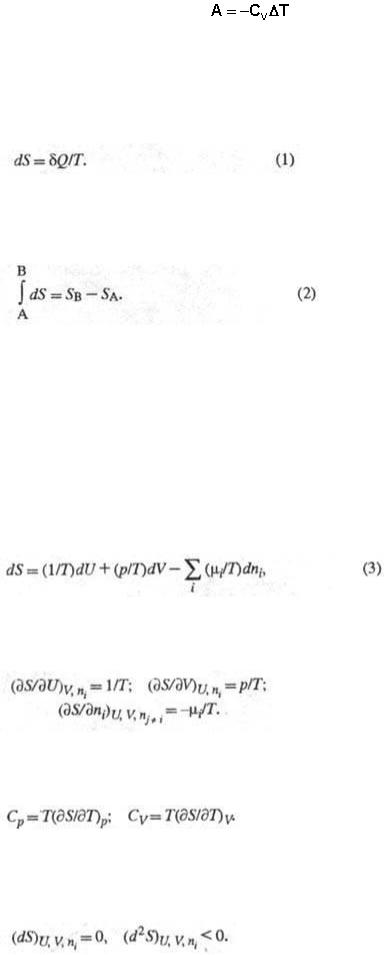
2. Энтропия, функция состояния S термодинамической системы, изменение которой dS для бесконечно малого обратимого изменения состояния системы равно отношению количества

теплоты полученного системой в этом процессе (или отнятого от системы), к абсолютной температуре Т:

Величина dS является полным дифференциалом, т.е. ее интегрирование по любому произвольно выбранному пути дает разность между значениями энтропии в начальном (А) и конечном (В) состояниях:

Теплота не является функцией состояния, поэтому интеграл от δQ зависит от выбранного пути перехода между состояниями А и В. Энтропия измеряется в Дж/(моль·град).

Понятие энтропии как функции состояния системы постулируется вторым началом термодинамики, которое выражает через энтропию различие между необратимыми и обратимыми процессами. Для первых dS>δQ/T для вторых dS=δQ/T.

Энтропия как функция внутренней энергии U системы, объема V и числа молей ni i-го компонента представляет собой характеристическую функцию (см. Термодинамические потенциалы). Это является следствием первого и второго начал термодинамики и записывается уравнением:

где р - давление, μi - химический потенциал i-го компонента. Производные энтропии по естественным переменным U, V и ni равны:

Простые формулы связывают энтропию с теплоемкостями при постоянном давлении Ср и постоянном объеме Cv:

С помощью энтропии формулируются условия достижения термодинамического равновесия системы при постоянстве ее внутренней энергии, объема и числа молей i-го компонента (изолированная система) и условие устойчивости такого равновесия:

10