(по цифровому вещанию) Dvorkovich_V_Cifrovye_videoinformacionnye_sistemy

Глава 19. Помехоустойчивое кодирование в системах передачи

степенях складываются по модулю два (без переноса в старший разряд), а операция вычитания эквивалентна сложению. Операция умножения на полином степени m соответствует сдвигу кодовой комбинации на m разрядов влево. Проиллюстрируем это на примере. Пусть m = 3 и полином v(x) = x3 +x2 +1 умножается на x3. Полиному v(x) = x3 + x2 + 1 соответствует комбинация 1101. Полиному v(x) = (x3 + x2 + 1) · x3 = x6 + x5 + x3 — комбинация 1101000.

19.3.2.Порождающая и проверочная матрицы циклического кода

Основным свойством циклических кодов является то, что все полиномы v(x), представляющие разрешенные кодовые комбинации, должны делиться без остатка на некоторый полином Gm(x) минимальной степени m, который называется порождающим полиномом кода [7.6, 7.9]. Следовательно, любое произведение Gm(x) на многочлены, степень которых не превышает k − 1, образует линейный циклический (n, k)-код. Свойство делимости комбинации циклического кода на порождающий полином положено в основу циклического кодирования и декодирования.

Как показано в [7.6], одним из основных свойств порождающего полинома Gm(x) является то, что он делит бином (xn + 1) без остатка. Таким образом, чтобы найти некоторый порождающий полином, необходимо знать разложение (xn + 1) на неприводимые множители φj (x), j = 1, l:

Многочлен φ(x) степени m является неприводимым в поле GF(2), если он не делится ни на какой многочлен с коэффициентами из GF(2) степени меньшей m, но большей 0.

В соответствии с (19.21) порождающим может быть полином, образованный как каждым неприводимым множителем φj (x), j = 1, l, так и любой комбинацией

их произведений, которые будут также являться делителями xn + 1:

$

Для компактной записи двоичного циклического кода (n, k)-кода используется порождающий (образующий) полином Gm(x) степени mn − k с коэффициен-

тами gi, i = 1, n − k из поля Галуа GF(2):

Gm(x) = g0 + g1x + g2x2 + · · · + gmxm.

Неприводимые полиномы играют роль, сходную с простыми числами в теории чисел. Вид неприводимого полинома зависит от числа проверочных символов m. Имеются таблицы неприводимых полиномов, некоторые из них представлены в табл. 19.3.

При больших значениях n двучлен xn + 1 может иметь несколько делителей степени m. В связи с этим возникает неоднозначность в выборе порождающего полинома: какой из этих делителей будет порождать наилучший код? На этот вопрос не существует однозначного ответа. Тем не менее во многих случаях целесообразно пользоваться таблицей наилучших двоичных циклических кодов, которые применяются в различных Рекомендациях ITU-T (табл. 19.4).

19.3. Циклические коды

Таблица 19.3. Таблица некоторых неприводимых полиномов

В соответствии с основным свойством циклических кодов, каждый многочлен циклического кода может быть представлен в виде произведения

v(x) = Ck(x) · Gm(x) = c0Gm(x) + c1xGm(x) + . . . + ck−1xk−1 Gm(x). (19.23)

Таблица 19.4. Таблица эффективных двоичных циклических кодов ITU

Учитывая произведение x5Gm(x), s = 0, k − 1, каждое слагаемое в (19.23) представляет собой сдвиг порождающего полинома Gm(x) на s элементов вправо, которому соответствует вектор

g = (1, g1, g2, . . . , gm−1, 1),

где g0 = 1 на основании соответствующего свойства полиномов минимальной степени [7.6]. В матричной форме кодовый вектор v, соответствующий многочлену V (x), может быть представлен в виде произведения информационного вектора c на порождающую матрицу Gk×n:

Каждая строка порождающей матрицы Gk×n имеет размерность n и является кодовым словом; в каждом столбце (19.26) присутствует циклический сдвиг вектора g=(1, g1, g2, . . . , gm−1).

19.3. Циклические коды

–подлежащая кодированию k-разрядная кодовая комбинация описывается полиномом Ck(x) степени k − 1;

–полином Ck(x) умножается на xm, что эквивалентно сдвигу k-разрядной комбинации влево (в сторону старших разрядов) на m разрядов или добавлению m нулей справа;

–полученный полином xmCk(x) делится на порождающий полином Gm(x), имеющий степень, равную числу проверочных символов m, в результате чего получается целая часть Q(x) и остаток от деления R(x)

–формируется n-разрядная разрешенная комбинация систематического циклического кода, соответствующая полиному v(x)xm Ck(x) + R(x), для чего в свободные разряды регистра записывается комбинация, соответствующая остатку от деления R(x).

Можно показать, что комбинации, соответствующие полиному v(x), являются разрешенными. С этой целью умножим обе части уравнения (19.32) на Gm(x):

Ck(x)xm = Q(x)Gm(x) + R(x).

Вычитая из обеих частей R(x) и учитывая, что операции вычитания и суммирования по модулю два эквивалентны, получим:

xmCk(x) + R(x) = Q(x)Gm(x).

Выражение в левой части этого равенства — это кодовое слово v(x). Следова-

тельно, v(x) = Q(x) — целая часть, т. е. полученный полином v(x) делится на

Gm(x)

Gm(x) без остатка, а значит, представляет собой разрешенную комбинацию циклического кода.

Пример. Построим кодовую комбинацию циклического кода (7, 4), соответствующую комбинации 1001. Общая длина комбинации n=7, число информационных символов k = 4, проверочных mn − k = 3. Из таблицы неприводимых полиномов табл. 19.3 для m = 3 выберем образующий полином G(x)x3 +x+1. В соответствии с рассмотренным выше алгоритмом кодирования получаем:

1. 1001 → C4(x) = x3 + 1. 2. x3C4(x) = x6 + x3.

Глава 19. Помехоустойчивое кодирование в системах передачи

19.3.4. Обнаружение ошибок

Процедура обнаружения ошибки сводится к делению принятой комбинации на порождающий полином Gm(x) и анализу остатка от деления R(x). Поскольку разрешенные кодовые комбинации делятся на образующий полином без остатка, то значение R(x) = 0 означает либо факт отсутствия ошибок, либо случай, когда кратность ошибки выше обнаруживающей способности циклического кода. Если R(x) = 0, то произошел прием с ошибкой (обнаруживаемой). Таким образом, остаток от деления R(x) играет роль синдрома в коде Хэмминга.

Пример процесса декодирования

Пусть полученная комбинация 1001110 совпадает с переданной, т. е. искажений нет. Известно, что комбинация образована с помощью порождающего полинома G3(x)x3 + x2 + 1. В результате деления полинома, описывающего эту комбинацию на порождающий полином G3(x) получается:

Пусть в результате приема искажен второй символ кода, т. е. принята комбинация 1101110. Тогда в результате расчета R(x) фиксируется ошибка:

x2 + x + x R(x) = 0.

19.3.5. Исправление однократных ошибок

Определение места ошибки в принятой комбинации циклического кода основано на анализе остатка R(x) от деления полинома v (x) принятой комбинации на порождающий полином Gm(x). Принятую с ошибкой в i-м разряде n-разрядную кодовую комбинацию можно представить полиномом:

v (x) = v(x) + xn−i,

где i = 1, n — номер искаженного разряда, отсчитываемый от старшего; v(x) — полином комбинации CRC–кода, принятой без ошибки; xn−i — полином однократной ошибки (ошибку можно представить как n-разрядную комбинацию с «1» в i-м разряде; например, при i = 2 и n = 5 ошибка представляется комбинацией 01000, которой соответствует полином x3).

Глава 19. Помехоустойчивое кодирование в системах передачи

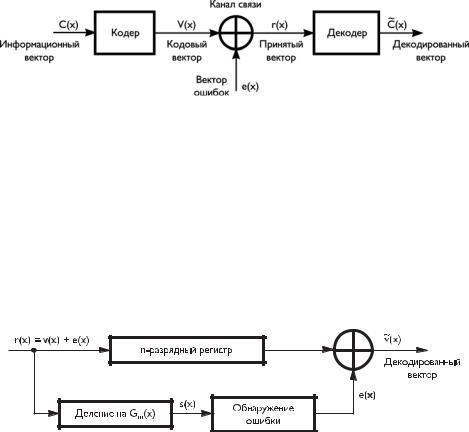
Рис. 19.11. Модель передачи данных по каналу связи с ошибками

В результате многочлен принятого кодового слова имеет вид:

или в соответствии с (19.31):

где s(x) является синдромом, представляющим собой остаток от деления r(x) на порождающий полином Gm(x):

Если r(x) является кодовым словом, то s(x) — нулевой многочлен. На рис. 19.12 представлена обобщенная структура декодера циклического кода.

Рис. 19.12. Обобщенная структура декодера циклического кода

Синдром s(x) используется для определения полинома ошибок e(x). Проблема декодирования в этом случае состоит в поиске полинома ошибок e(x) по известному синдрому s(x) согласно уравнению (19.35). При наличии многократных ошибок задача декодирования будет рассматриваться уже как решение системы уравнений вида (19.35). Эффективная реализация алгоритмов декодирования циклических кодов, позволяющих обнаруживать и исправлять многократные ошибки, достигается при использовании арифметики конечного поля — поля Галуа.

19.3.7. Арифметика полей Галуа

Возможность построения хороших циклических кодов определяется умением находить порождающие полиномы. В настоящее время существует ограниченное количество методов конструирования порождающих полиномов циклических кодов с предсказуемой исправляющей способностью и приемлемой скоростью кодирования. Наиболее известный из методов конструирования порождающих полиномов основан на теории полей Галуа.

Как известно, в обычной алгебре операции сложения/вычитания и умножения/деления могут дать результат, который выходит за пределы некоторого за-

19.3. Циклические коды

данного диапазона. В конечном поле любые операции с любыми элементами этого поля в результате дают элемент, принадлежащий этому же полю. Соответственно, в конечных полях вообще отсутствуют такие проблемы, как переполнение при умножении и потеря точности при делении, делая тем самым алгебру GF наиболее естественной с точки зрения компьютерных вычислений, которые имеют конечную разрядность. Конечное поле — это некоторая ограниченная совокупность чисел, над которыми определены четыре арифметические операции, результат выполнения которых не выходит за пределы этой совокупности.

Пример. Рассмотрим построение поля Галуа GF(28), состоящее из q = 28 = = 256 чисел от 0 до 28 − 1, упорядоченных особым образом.

Согласно теории Галуа, любой элемент произвольного поля можно представить в виде i-й степени одного (или нескольких) примитивного элемента α: bi = αi GF (p), 0 i p − 2. В поле GF(28) имеется единственный примитивный элемент, в качестве которого выступает простое число 2. Следовательно, любой ненулевой элемент поля bi может быть получен возведением 2 в степень

где ξ — некоторое число, которое в теории Галуа задается в полиномиальной форме.

Для примера, поле GF(28) может быть порождено полиномом f (x)x8 + x4 + x3 + x2 + 1, который используется в коде Рида–Соломона (204, 188) на физическом уровне телевизионного стандарта DVB-T. Этот полином соответствует в двоичной форме числу ξ = 0011101B и в десятичной — ξ = 285.

Согласно теории [7.7, 7.8], любой порождающий поле полином f (x) должен быть неприводимым. Таким образом, конечное поле вида GF(2m) может быть построено заданием некоторого двоичного неприводимого полинома f (x) порядка m, который по смыслу соответствует роли порождающего полинома Gm(x) циклических кодов.

Элементы теории полей Галуа

Поле — это множество элементов A, в котором определены операции сложения, вычитания, умножения и деления. Сложение и умножение должны удовлетворять коммуникативному, ассоциативному и дистрибутивному законам: для любых элементов α, β, γ. В таком поле должны выполняться соотношения:

–коммутативность: α + β = β + α; α · β = β · α;

–ассоциативность: α + (β + γ) = α + β) + γ; α · (β · γ) = (α · β) · γ;

–дистрибутивность: α · (β + γ) = α · β + α · γ;

–замкнутость: α + β A,

Глава 19. Помехоустойчивое кодирование в системах передачи

атакже должны существовать элементы 0, 1, −α, обратный к α = 0 элемент α−1, такие, что:

Число элементов конечного поля называется порядком поля. Согласно теории [7.8], число элементов q конечного поля всегда удовлетворяет условию

где p — простое число, называемое характеристикой поля; m = 1, 2, . . .. Другими словами, если число элементов q некоторого множества не удовлетворяет условию (19.36), то для этого множества невозможно определить операции сложения и умножения, удовлетворяющие аксиомам поля. Так, например, невозможно образовать поле с числом элементов, равным 6, 10, 12, 14 и т. д., но можно построить поле с числом элементов, равным 2, 3, 4, 5, 7, 8, 9, 11 и т. д.

Наиболее просто операции сложения и умножения выполняются в поле с числом элементов, равным p (m = 1). В этом случае поле называется простым; операции сложения и умножения в нем определены по модулю p ( mod p), а сами элементы образуют последовательность чисел {0, 1, 2, . . . , p − 1}. Простейшим простым полем Галуа является двоичное поле GF(2), сложение и умножение в котором выполняются по правилам арифметики «по модулю 2». Можно заметить, что правила арифметики табл. 19.1 удовлетворяют перечисленным выше правилам, с учетом того что обратным элементом к «1» по сложению и умножению является сам элемент «1».

Сложнее обстоит дело с построением расширенных полей Галуа GF(pm), где m > 1. Так как теория помехоустойчивого кодирования основывается, как правило, на полях характеристики 2, то ниже будут рассматриваться основные методы построения полей GF(2m). Каждый элемент такого поля можно представить в виде слова длины m над GF(2) или многочлена с двоичными коэффициентами, степень которого меньше чем m. К примеру, любой элемент α GF(23) можно записать как двоичное слово или как многочлен a2x2 + a1x + a0, {a2, a1, a0} {0, 1}, где формальная переменная x является указателем позиции соответствующего коэффициента. В этом случае, если сложение элементов из GF(2m) будет выполняться по правилу сложения представляющих их многочленов в поле GF(2), а умножение элементов поля определить как умножение представляющих эти элементы многочленов по модулю некоторого заданного неприводимого многочлена над GF(2) степени m, то тем самым будет построено поле Галуа GF(2m).

Если рассмотреть степени некоторого ненулевого элемент α GF(q) вида α1, α2, . . . , αl, . . ., то нетрудно заметить, что все они являются элементами поля GF(q) и в силу конечности поля для некоторых l и s (l = s) будет справедливо равенство αl = αs, а значит, αl−s = 1. Минимальное натуральное число dα, для которого αdα = 1, является мультипликативным порядком элемента α.

В теории конечных полей доказывается, что мультипликативный порядок любого ненулевого элемента α поля GF(q) делит значение q − 1. Например, в поле GF(23) число ненулевых элементов поля является простым: q − 1 = 7, следовательно, делителями q − 1 могут быть только 1 и 7. В свою очередь, это означает, что все ненулевые элементы, кроме единичного, имеют максимальный мультипликативный порядок, равный 7.

19.3. Циклические коды

Элемент α поля GF(q), имеющий максимальный мультипликативный порядок dαq − 1, называется примитивным элементом поля.

В любом конечном поле GF(q) всегда существует хотя бы один примитивный элемент α. Особенностью такого элемента является то, что все его q − 1 последовательных степеней α1 = α; α2, . . . , αq−2, αq−1 = 1 различны и соответствуют всем ненулевым элементам поля GF(q). Таким образом, в поле GF(23) все ненулевые элементы поля, за исключением единицы, примитивны, поскольку число ненулевых элементов является простым и, следовательно, мультипликативный порядок для этих элементов максимален и равен 7.

Расширенное поле, построенное как множество полиномов по модулю некоторого неприводимого полинома f (x), всегда содержит в качестве элемента поля полином x. Если окажется, что x — примитивный элемент, то соответствующий неприводимый полином f (x) называется примитивным полиномом. Примитивный элемент α, степени которого образуют конечное поле, является корнем неприводимого полинома f (x):

и, как будет показано ниже, удовлетворяет условию αq−1 = 1.

Примитивные полиномы произвольной степени m определены над любым конечным полем. Они наиболее удобны для построения расширенных полей, поскольку позволяют реализовать простой вариант таблицы умножения элементов поля. Действительно, любые ненулевые элементы a и b расширенного поля GF(2m) могут быть выражены как некоторые l-я и s-я степени примитивного элемента α: a = αl, b = αs. Тогда a · b = αl+s и, значит, таблица умножения двух элементов поля a и b представляет собой не что иное, как перечисление всех ненулевых степеней примитивного элемента α.

Построение расширенного поля

Построение расширенного поля GF(pm) в виде степеней примитивного элемента является достаточно простой процедурой и предполагает следующий алгоритм действий.

На первом этапе выбирается порождающий поле примитивный полином степени m над простым полем GF(p): f (x)xm + fm−1xm−1 + · · ·+ f1x + f0. Тогда m-я степень x по модулю f (x) определится как

xm = −fm−1xm−1 − fm−2xm−2 − . . . − f1x − f0.

Предположение о примитивности x позволяет использовать для его обозначения α, в результате чего имеем равенство

Если основным является поле с характеристикой p = 2, то в силу свойств двоичной арифметики поля GF(2)α = −α, и выражение (19.38) можно записать в виде