
- •Расчет и конструирование панелей покрытий.
- •Расчет и конструирование балок покрытий.
- •Основы расчета ферм покрытия – нагрузки на ферму, учет внеузлового приложения нагрузки. Расчетные длины сжатых элементов, принципы расчета сжатых и растянутых элементов ферм.
- •Принципы армирования узлов ферм. Расчет опорного узла фермы.
- •Принципы армирования узлов ферм. Расчет промежуточного узла фермы.
- •Цилиндрические оболочки тпк покрытий. Классификация. Основы упругого расчета длинных оболочек. Усл примен метода предельного равновесия к расчету длинной оболочки.
- •Расчет длинной цилиндрич оболочки методом пред равновесия. Эпюры усилий в оболочке, принципы армирования.
- •Основы расчета и конструир коротких цилиндрических оболочек.
- •Основы расчета и конструирования призматических складок.
- •Конструктивные решения, основы расчета и конструирование цилиндрических резервуаров.
- •Конструктивные решения, основы расчета и конструирования прямоугольных резервуаров.
- •Основные положения расчете и конструировании водонапорных башен.
- •Основные положения о расчете и конструировании силосов.
- •Основы расчета и конструирования бункеров.
- •Основы расчета и конструирования подпорных стен.
-
Принципы армирования узлов ферм. Расчет опорного узла фермы.
Требуемая площадь поперечного сечения продольных ненапрягаемых стержней в нижнем поясе в пределах опорного узла:
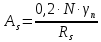

Длина
заделки
 .
Расчетное усилие из условия прочности
в наклонном сечении по линии отрыва АВ:
.
Расчетное усилие из условия прочности
в наклонном сечении по линии отрыва АВ:

Расчетное
усилие в продольной напрягаемой арматуре:

 -
длина заделки сварного каркаса нижнего
пояса фермы;
-
длина заделки сварного каркаса нижнего
пояса фермы;
 - длина заделки, обеспечивающая полное
использование прочности продольной
напрягаемой арматуры. Расчетное усилие
в продольной не напрягаемой арматуре:
- длина заделки, обеспечивающая полное
использование прочности продольной
напрягаемой арматуры. Расчетное усилие
в продольной не напрягаемой арматуре:
 Площадь
сечения одного поперечного стержня:
Площадь
сечения одного поперечного стержня:
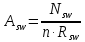 где:
где:
 -
количество поперечных стержней в узле,
пересекаемых линией АВ (при двух каркасах
и шаге стержней 80 мм.) Из условия
обеспечения прочности на изгиб в
наклонном сечении (по линии АС) требуемая
площадь поперечного стержня:
-
количество поперечных стержней в узле,
пересекаемых линией АВ (при двух каркасах
и шаге стержней 80 мм.) Из условия
обеспечения прочности на изгиб в
наклонном сечении (по линии АС) требуемая
площадь поперечного стержня:


где:
 высота сечение опорного узла;
высота сечение опорного узла;
 высота сечение нижнего пояса.
высота сечение нижнего пояса.
 длина
опорного узла;
длина
опорного узла;
 - усилие в приопорном стержне верхнего
пояса.
- усилие в приопорном стержне верхнего
пояса.
Определяем высоту сжатой зоны бетона:

 -
расстояние от центра тяжести сжатой
зоны бетона до равнодействующей усилий
в поперечной арматуре опорного узла.
-
расстояние от центра тяжести сжатой
зоны бетона до равнодействующей усилий
в поперечной арматуре опорного узла.
Проверяем условие прочности на изгиб в наклонном сечении.
-
Принципы армирования узлов ферм. Расчет промежуточного узла фермы.
Фактическая
длина заделки стержней раскоса за линии
АВС:
 ,
,

Требуемая
длина заделки

Необходимое сечение поперечных стержней каркасов определяем по формуле

где:
 – условное увеличение длины заделки
растянутой арматуры, при наличии на
конце коротыша или петли;
– условное увеличение длины заделки
растянутой арматуры, при наличии на
конце коротыша или петли;
 -
количество поперечных стержней в узле,
пересекаемых линией АВС (при двух
каркасах и шаге стержней 100 мм.);
-
количество поперечных стержней в узле,
пересекаемых линией АВС (при двух
каркасах и шаге стержней 100 мм.); – учитывает особенности работы узлов,
для узлов верхнего пояса;
– учитывает особенности работы узлов,
для узлов верхнего пояса;
 - учитывает особенности работы узлов,
для узлов нижнего пояса;
- учитывает особенности работы узлов,
для узлов нижнего пояса;
 – интенсивность использования арматуры
– интенсивность использования арматуры

Проверяем условие прочности. Площадь сечения окаймляющего стержня в промежуточном узле определяем по условному усилию:
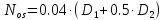
 -
усилия в растянутых раскосах, а при
наличии только одного растянутого
раскоса. Площадь сечения окаймляющего
стержня:
-
усилия в растянутых раскосах, а при
наличии только одного растянутого
раскоса. Площадь сечения окаймляющего
стержня:

где:
 - во всех случаях, установлено из условия
ограничения раскрытия трещин;
- во всех случаях, установлено из условия
ограничения раскрытия трещин;
 - число каркасов в узле или число огибающих
стержней в сечении;
- число каркасов в узле или число огибающих
стержней в сечении;
В узлах, где примыкают сжатые раскосы и стойки, проектируем поперечные стержни из конструктивных соображений ∅6 А-400 с шагом 100мм, a окаймляющие стержни ∅10 А-400
-
Напряженное состояние оболочек ТПК – компоненты безмоментного и моментного состояния, количественное соотношение между состояниями по поверхности ТПК. Принципы расчета оболочек по моментной и безмоментной теориям.
Теории
оболочек в завис от напряж сост делятся:
безмомент, полумомент, моментная. Примен
теории зависит от: гауссовой кривизны;
наличия на пов-ти оболочки линии скольж
напряж сост,т.е. места где физ хар-ки
измен скачком. Вблизи этих мест возник
доп напряжения, так называемый краевой
эффект и нельзя использ безмомент
теорию. После образ трещин по мере роста
нагр и напр в бетоне и ар-ре в них нарастают
нелинейные деформации вплоть до стадии
предельного равновесия. В общем случае
в нормальных сечениях оболочек возникают
нормальные силы Nη
и Nξ,
касательные
силы Νηξ
и Nξn,
; Mη
и Мξ,
; Qη
и Qξ,
крутящие
моменты Hη
и Hξ
Им соответствуют
проекции сил и моментов в элементе ед
размеров в основании оболочки. Тонкостенные
оболочки имеют малую жесткость на изгиб
в сравнении с жесткостью против действия
сил, развивающихся в срединной поверхности.
Поэтому внешним нагрузкам, действующим
перпенд срединной повер-ти оболочки,
противодействуют Nη,
Νξ
Nηξ
(на 92...98%). Доп
часть нагр, (2...8%) воспринимают компоненты
изгибного состояния Мх,
Му,
Мху,
Qx,
Qy.

Безмомент напряж сост ТПК описывается ур-нием равновесия на ось οz нагр и внутр сил, отнесенных к элементу единичных размеров основания оболочки:
![]() q-нагр,
непрерыв распред на пов-ти.
q-нагр,
непрерыв распред на пов-ти.
kx,
ky
-кривизны
пов-ти. Сост общего изгиба оболочки
развив по всей ее области, и сост местного
изгиба - в ее отдельных частях, где наблюд
скачкообраз изм нагр,примыкан к контурным
констр . Общее изгибное сост:
цилиндрич
жесткость оболочки на изгиб в напр оси
x
равна:

Dx = EIx(l - ν2) ≈EI (поскольку для бетона при сжатии ν ≈ 1/6, при растяжении ν ≈ 1/10), а в направлении оси у равна:
Dy = EIy(l - v2) ≈ EIy. В этих ф-лах Nx(xy) и Ny(x,y) - функции внутр сил Nx и Ny, кот могут быть взяты из решения по безмомен состоянию оболочек. Величина I - момент инерции сечения оболочки; для оболочек гладких (без ребер) I = h3/12 (для прямоугольного сечения при длине его равном единице).
