Потенциалы простейших электрических полей.
Из соотношения
,
определяющего связь между напряженностью
и потенциалом электрического поля,
следует формула для вычисления потенциала
поля:
где интегрирование производится вдоль силовой линии поля; С – произвольная постоянная, с точностью до которой определяется потенциал электрического поля.
Если направление
поля
совпадает с направлением радиус–вектора
(
),
то вычисления можно производить по
формуле:
.
Рассмотрим ряд примеров на применение этой формулы.
Пример1.
Потенциал поля точечного заряда
(рисунок).
При
полагают, что
,
тогда
.
Таким образом, потенциал поляточечного
заряда
определяется по формуле:
Пример 2. Потенциал поля металлического заряженного шара.
а)
Изолированный шар
(рисунок).
при
,
т.е. внутри шара
=const.
Вне
шара
.
При
φ = 0, следовательно, С = 0.
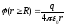- вне шара.
Для определения
используем свойство непрерывности
потенциала: при переходе через границу
поверхности шара, потенциал не претерпевает
скачка. Полагая в последней формулеr
=R,
находим:
- внутри шара.
б) Заземленный шар (рисунок).
.
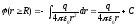При
,
то есть
- вне шара.
Внутри шара φ(r ≤ 0) = φ0 = 0. Разность потенциалов U двух точек на силовой линии электрического поля заряженного шара определяется по формуле:
.
Пример
3. Потенциал
поля заряженной нити (рисунок).
При
:
В итоге получаем:
Разность потенциалов U (рис.2.17) двух точек на силовой линии поля заряженной нити:
Пример
4. Потенциал
поля заряженной плоскости (рисунок).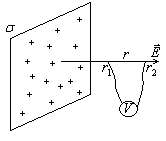
Разность потенциалов U (см. рисунок) двух точек на силовой линии поля заряженной плоскости:
.
Проводники в электростатическом поле
Опыт показывает,
что при равновесии электрические заряды
распределяются на внешней
поверхности
проводников (см. рисунок). Поэтому,
согласно теореме Гаусса, электрическое
поле внутри проводника
,
а потенциал φ
= const.
Рисунок. Опыт, иллюстрирующий равновесное распределение зарядов на проводнике.
Из сказанного
следует, что при равновесии зарядов
поверхность проводника является
эквипотенциальной.
Вблизи поверхности заряженного проводника
силовые линии перпендикулярны его
поверхности, и поэтому работа по
перемещению заряда вдоль любой линии
на поверхности проводника
.
При внесении незаряженного проводника в электрическое поле на его внешней поверхности появляются индукционные заряды противоположного знака, электрическое поле которых компенсирует внутри проводника внешнее поле. На этом свойстве проводников основано действие электростатической защиты.
Электроемкость проводников. Конденсаторы.
Заряд q, сообщенный уединенному проводнику создает вокруг него электрическое поле, напряженность которого пропорциональна величине заряда. Потенциал поля φ, в свою очередь, связан с напряженностью поля также пропорциональной зависимостью. Следовательно, заряд и потенциал уединенного проводника связаны между собой линейной зависимостью:
q = Cφ
Коэффициент пропорциональности С называется электроемкостью (или просто емкостью) проводника. Емкость проводника зависит от его формы и размеров, а также свойств окружающей проводник среды. Если проводник находится в непроводящей среде с диэлектрической проницаемостью ε, то его емкость увеличивается в ε раз.
Единицы измерения электроемкости в СИ:
Пара проводников, между которыми имеется разность потенциалов, называется простейшим конденсатором. Индуцированные на проводниках заряды равны по величине и противоположны по знаку. Заряд каждой пластины по абсолютной величине
Если пространство между проводниками заполнено средой с диэлектрической проницаемостью ε, то
где С0 - емкость конденсатора в вакууме.
Вычислим емкость простых конденсаторов.
Согласно определению, емкость конденсатора:
,
где
(интеграл берется вдоль силовой линии поля между обкладками конденсатора).
Следовательно, общая формула для вычисления емкости любого конденсатора есть:
Рассмотрим ряд примеров на применение этой формулы.
Пример 1. Емкость плоского конденсатора (рисунок ниже).
Рис.4.3. Плоский
конденсатор.
,
Здесь S – площадь одной пластины. В итоге получаем
Пример 2. Емкость цилиндрического конденсатора (рисунок ниже).
Рисунок. Цилиндрический конденсатор.
Мы имеем
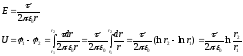
l
Заряд
равен:
,
l
– длина конденсатора; r1,
r2-радиусы
электродов
.
+
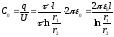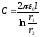
Пример 3.
Емкость сферического конденсатора и
уединенного шара (рисунок 
ниже).
Рисунок. Сферический конденсатор.
Уединенный
шар может рассматриваться как сферический
конденсатор при
и
:
Рисунок. Уединенный шар.
В итоге имеем:
