Лева_2.0 / Lab05_Excel

Расчётно-графисечкие работы в MS Excel Стр. 1 из 13

таблице 1 приложения. На защиту лабораторной подготовить лист электронной книги Excel по образцу на рисунке 1.

Ход работы:

1)Запустить программу Excel. Создать документ Книга1. Сохранить в свою папку на жестком диске под оригинальным именем, например, Книга Иванова, переименовать лист Лист1 на Лаб №.

2)Создать заголовок сверху по центру будущей таблицы, используя шрифты помельче, 12 пунктов, Аrial курсив и покрупнее, 14 пунктов, Times полужирный. Выделить название темы лабораторной цветом.

3)Сделать подпись Выполнил, Дата, Вариант. Дата должна пока-

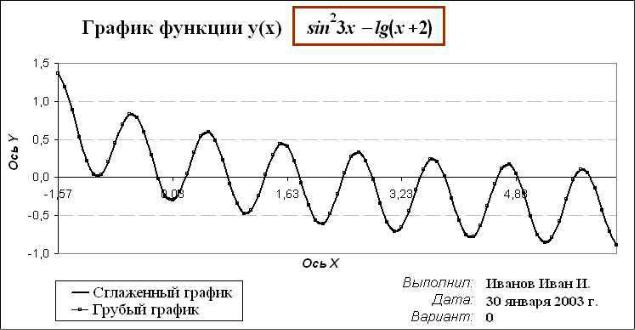
Здесь скрыты строки с 16 по 83 для экономии места на рисунке.

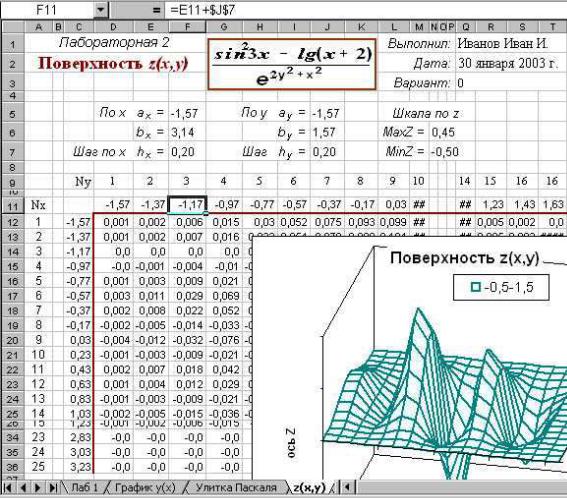
Рисунок 1. Образец оформления лабораторной работы

на листе Excel (для 0-го варианта)

1

зывать текущую дату в заданном полном формате. Вставить свою функцию по варианту в математической нотации как объект MS Equation. Выделить формулу цветной рамкой.

4)Завести отдельные ячейки для начала интервала аx и шага табулирования hx, ячейки D7 и D8 на рисунке 1. Начало интервала определить через функцию ПИ(). Для заполнения диапазона ячеек со значениями аргумента функции использовать абсолютные адреса этих ячеек. В ячейки C7 и C8 вставьте пояснения Начало интервала аx =

иШаг hx =.

5)В строке 10 оформить шапку таблицы: Номер точки, Значение аргумента, Значение функции, и ниже, в строке 11 сокращенно: №, х, у.

6)Заполнение таблицы.

Создание столбца номеров точек. Набрать 1 в В12. Протащить маркер заполнения формул с нажатым Ctrl до 79 в всплывающем окне для получения арифметической прогрессии с приращением 1 в диапазоне ячеек B13:B90.

Создание столбца х. В первую сверху ячейку столбца, С12 набираем ссылку на начало интервала =$D$7 (абсолютный адрес). Под ней в ячейку C13 формулу для расчета следующего значения аргумента через предыдущее =C12+$D$8 (комбинация абсолютных и относительных адресов). Протаскиваем маркер заполнения через диапазон ячеек C14:C90 для получения в нем формул расчета значений аргумента.

Создание столбца y. В ячейку D12 набираем формулу расчета функции по варианту для первой строки таблицы. Для 0-го варианта =sin(3*C12)^2-log10(C12-2) (относительный адрес х). Далее используем технику протаскивания формулы для заполнения диапазона ячеек D13:D90 со значениями функции.

7)Форматирование таблицы. Вывести 5 значащих цифр для значений х и 10 для у. Выровнять по десятичной точке. Применяя условное форматирование, назначить холодный цвет (цвет шрифта, а не заливки), например, синий, отрицательным значениям и красный положительным. Навести рамки в таблице по образцу на рисунке 1.

8)Внизу под таблицей посчитать значения функции для х=0.0 и х=1.0. Ответы для контроля приведены в таблице 2 приложения.

9)Посчитать максимальное Ymax и минимальное Ymin значения функции в полученном диапазоне ячеек.

10)Сохранить книгу для использования в следующих лабораторных работах.

2

Задание 2: Построить график кривой f (t) , заданной параметрически, и несколько вложенных в нее кривых.

Задание 3: Построить график трёхмерной поверхности z(x,y).

Вид функций и интервалы выбираются по варианту из таблиц 1, 3 Приложения.

Ход работы:

Построение на одних осях двух графиков функции y(x), x [ax,bx] ломаной линией и сглаженной.

1)График функции в Excel, как и все остальные диаграммы, строится по дискретным значениям. Исходные данные для графика получены в предыдущей лабораторной Лаб №[Книга Иванова].

2)Запускаем Мастера диаграмм. Выбираем тип диаграммы График. Во втором окне мастера указываем исходные данные для

первого ряда Значения: столбец y, Подписи оси Х: столбец x, Имя: набираем с клавиатуры Грубый график. Для второго ряда Значения и Подписи по оси Х те же, Имя: Сглаженный график. Лишние ряды удалить.

3) Отформатировать график по образцу рисунка 2.

На грубом графике соединить точки отрезками прямых сплошными, тонкими, синего цвета, в точках синие прозрачные квадратные маркеры 5 пунктов. На глаженном графике - соединяющие точки линии сплошные, толстые, красные, сглаженные, без маркеров. Настроить порядок рядов так, чтобы тонкие синие линии были видны на фоне красных. Оформить график заголовком, Equation скопировать с листа Лаб1 на график. Подписать оси как Ось Х и Ось Y. Ось Х провести че-

рез y=0. Проредить деления шкал, в подписях делений отобразить 2-3 цифры, чтобы не загромождали график. Настроить диапазон оси Y от ~Ymin до ~Ymax своей функции. Подпись Выполнил Дата Вариант подставить в шесть надписей из соответствующих ячеек листа. Выровнять и распределить надписи инструментами панели Рисование – Действия – Выровнять, Распределить, Группировка. Убрать серую заливку фона области построения. Линии сетки оставить только горизонтальные по основным делениям оси Y, уменьшить их яркость до штрих светло-серого цвета.

3

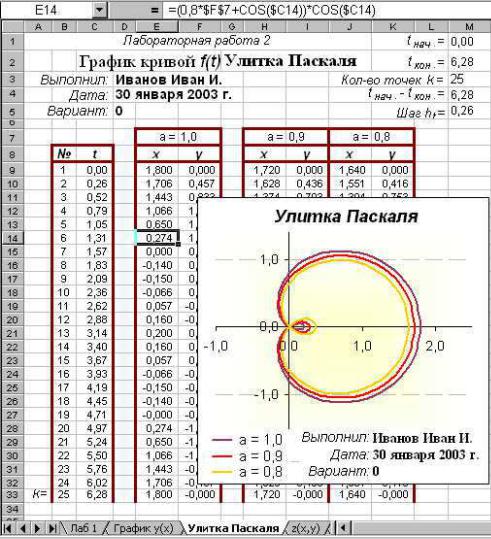
Рисунок 2. Образец оформления графика функции y(x)

4) Работа с книгой. Перенести диаграмму на отдельный лист под именем График y(x). Для обзора точности построения ломаной и сглаженной линий отобразить график в максимальном масштабе.

Построение графика кривой f(t), заданной параметрически, и

вложенных кривых при a=0.9, 0.8, 0.7,..

5)Задание выполняется на отдельном листе. Дать листу имя по названию кривой, Улитка Паскаля для 0-го варианта.

6)Предварительно перед построением графика рассчитать таб-

лицу значений x(t,a), y(t,a), комбинируя абсолютные и относительные

адреса ячеек со значениями t и а. Шаг по t подсчитать на этом же листе, чтобы можно было его изменить, если потребуется улучшить качество кривой. Достаточно взять 20 – 30 значений параметра t, диа-

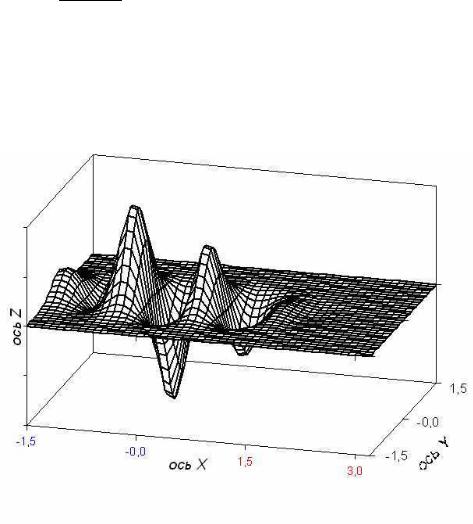
грамма не будет их использовать, они нужны для расчета x,y- координат точек кривой. Примерный вид таблицы рассчитанных для графика данных смотри на рисунке 3. В строке формул показана фор-

мула в выделенной ячейке Е14 для x-координаты шестой точки при

t=1.31 кривой а=1.0.

7) Неоднозначные или с неравномерным шагом по аргументу кривые строятся по точкам на диаграммах типа Точечная. Запускаем Мастера диаграмм, выбираем тип диаграммы Точечная, подтип сглаженные линии без маркеров. Точечная диаграмма - это составная диаграмма, одна точка данных составляется из двух ячеек со значе-

4

ниями её x, y координат. То есть исходными данными для одного ряда будет диапазон из двух столбцов. Обратите внимание, что диапазон ячеек для первой кривой окружен пустыми клетками, чтобы Excel автоматически распознал непрерывный диапазон исходных данных ='Улитка Паскаля'!$E$9:$F$33, необходимо только перед вызовом Мастера диаграмм установить курсор внутри этого диапазона. Тогда окно предварительного просмотра мастера дает удовлетворительную картинку уже на первом шаге. В качестве имени ряда взять значение

а=1.0. На остальных шагах Мастер диаграмм может сделать название диаграммы, заголовки осей, размещение легенды и самой диаграммы.

8) Ручная доводка диаграммы. Заливка области построения обычная белого цвета. Настроить шкалы осей: цену основных деле-

Рисунок 3. Вид таблицы значений x(t,a), y(t,a) и образец оформления графика f(t)

5

ний подобрать так, чтобы было 3 – 4 подписи на оси, в числовом формате подписей делений ограничиться одним знаком после запятой. Из формата выделенного ряда или ключа легенды настроить толщину и цвет линии – сглаженная, максимальной толщины, цвет красный, убрать маркеры точек.

9) Добавляем на диаграмму вложенные кривые. В окне Исходные данные на вкладке Ряд добавляем ряды, задавая диапазоны зна-

чений x и y. Например, для кривой а=0.9 Значения Х: ='Улитка Паска-

ля'!$H$9:$H$33, Значения Y: ='Улитка Паскаля'!$I$9:$I$33, Имя: ='Улитка Паскаля'!$H$7:$I$7. в окне предварительного просмотра сразу появляются кривые и их имена в легенде. Задать цвета кривым в

стиле Домна, плавно меняющиеся от красного для а=1.0 через оран-

жевые тона до желтого для последнего a.

Построение проекции графика функции двух переменных

z( x , y ) = y( x ) , x [-π/2; π], y [-π/2; π/2],

e x 2 +2 y2

где y(x) выбирается по варианту из таблицы 1 приложения. Образец графика поверхности представлен на рисунке 4.

1)Заводим новый лист под именем z(x,y).

2)Строим таблицу значений x, y и z. Размещаем ее из сообра-

Рисунок 4. 3D-график функции z(x,y)

6

жений удобства работы на листе: чтоб она была компактная, то есть занимала меньше места на листе, чтобы направления роста х и у совпадали с направлением осей правосторонней системы координат. Образец на рисунке 5. Качество картинки зависит от шага, с которым посчитаны значения z(x,y). Поэтому рекомендуется разместить шаги изменения переменных на листе и использовать их адреса при расчете

xи y. Для начала возьмем hx=hy=0.2.

3)Устанавливаем курсор в диапазон значений z, запускаем Мастера диаграмм, заказываем тип Поверхность, единственный существенно трехмерный из стандартных автоформатов. Здесь каждая точка

данных составляется из трех ячеек с х, у и z значениями, где х и у задают равномерную сетку и расположены в первом столбце и первой строке прямоугольного диапазона.

4) Отказываемся от перспективного изображения Диаграмма – Объемный вид – Изометрия. Убираем серый фон стен и основания.

Рисунок 5. Образец расчёта данных для трёхмерного графика z(x,y)

7

Прореживаем деления и подписи осей. Формат оси категорий (оси X) – Шкала – Число категорий между делениями – увеличить - 8. И сразу убираем Пересечения с осью значений между категориями, это используется на гистограммах. Формат оси рядов (оси Y) – Число рядов между делениями – увеличить - 8. Формат оси значений (оси Z) – Вид

–Основные деления – Нет, Шкала – Цена основных делений >> ZmaxZmin, так как они задают не только деления оси значений, но и шкалу раскраски поверхности. И чтобы были деления на оси Z: Вид – Промежуточные деления – Наружу, Шкала - Цена промежуточных делений

–0.5.

5)Ключ легенды является ключом к раскраске поверхности. Выберите способ заливки поверхности посветлее или даже штриховым узором и в тон потемнее цвет линий сетки. Улучшает качество изображения подсветка: Формат ключа легенды - Параметры - Объемное заполнение.

Дополнительные задания

1)Улучшить внешний вид графика y(x) градиентной заливкой области построения.

2)Градиентная заливка центра фигуры, ограниченной замкнутой кривой f(t).

3)Построить поверхность z(x,y) с более мелким шагом по x и y. hx=hy=0.1. Образец на рисунке 4.

8

9

Контрольные ответы