2.2.5. Динамика вращательного движения твёрдого тела

1. Основной закон (основное уравнение) динамики вращательного движения твёрдого тела относительно неподвижной оси

где – результирующий момент всех внешних сил относительно оси вращения; – момент импульса (момент количества движения) твёрдого тела относительно оси вращения

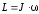где J – момент инерции твёрдого тела относительно той же оси вращения.

2. Основной закон динамики вращательного движения при J = const

где – угловое ускорение тела.

3. Основной закон динамики вращательного движения для среднего значения момента силы

где – изменение угловой скорости за промежуток времени.

4. Момент силы относительно оси вращения:

где l – плечо силы (кратчайшее расстояние от оси вращения до линии действия силы F); – угол между направлением действия силы и радиус-вектором, проведённым от оси вращения к точке приложения силы.

5. Момент инерции материальной точки относительно заданной оси:

где m – масса материальной точки; r – расстояние её до оси вращения.

6. Моменты инерции некоторых тел массой m относительно оси, проходящей через центр симметрии:

а) стержня длиной l относительно оси, перпендикулярной стержню

;

б) обруча (тонкостенного цилиндра) радиуса R относительно оси, перпендикулярной плоскости обруча (совпадающей с осью цилиндра)

;

в) диска радиуса R относительно оси, перпендикулярной плоскости диска

;

г) шара радиуса R относительно оси, проходящей через центр шара

Примеры решения задач

Задача 1

К ободу однородного сплошного диска радиусом 0,5 м приложена постоянная касательная сила 100 Н. При вращении диска на него действует момент сил трения . Определить массу диска, если известно, что его угловое ускорение постоянно и равно 16 рад/с².