процессы -гидравлические / гидравлические / гидравлические / 2.1. Насосные установки (3 часть)

В

Рис 2.24. Схема водокольцевого насоса:

1 – водяное кольцо; 2 – нагнетательное отверстие; 3 – напорный патрубок; 4 – всасывающий патрубок; 5 – корпус; 6 – рабочее колесо; 7– секторное отверстие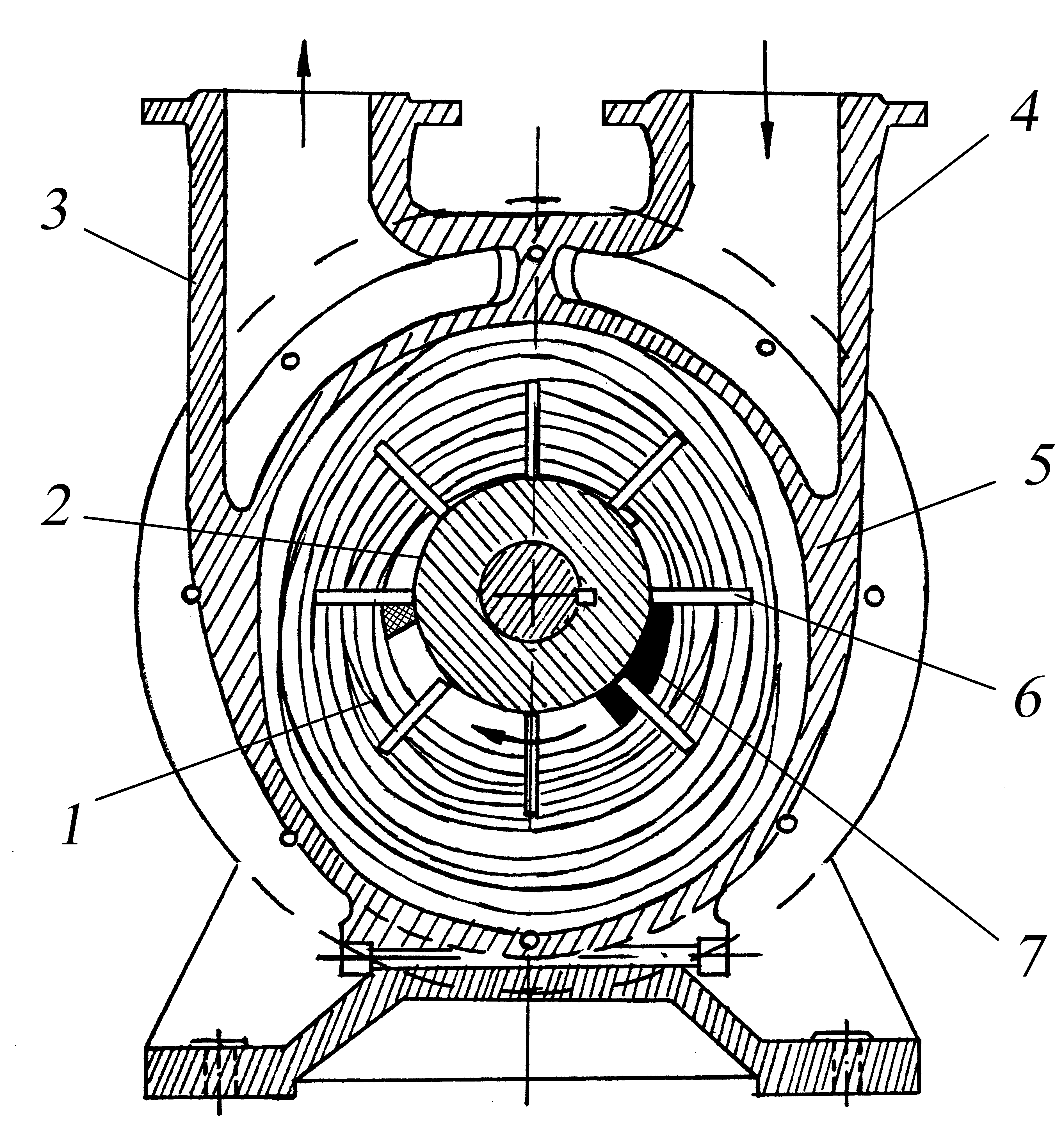

акуумные насосы (вакуум-насосы) предназначены для откачки воздуха из всасывающих линий центробежных насосов при заливе их водой перед пуском, а также тогда, когда требуется удалить воздух из системы и создать вакуум. Наибольшее распространение получили водокольцевые вакуум-насосы, (рис 2.24). На валу насоса закреплено колесо с радиальными лопатками 6, расположенное эксцентрично по отношению к цилиндрической камере корпуса 5. Возле ступицы колеса имеются два серповидных выреза а и б, соединенных соответственно с напорным 3 и всасывающим 4 патрубками насоса.

Если перед пуском насоса в его корпус 5 залить воду, то при вращении рабочего колеса 6 образуется водяное кольцо 1, расположенное концентрично по отношению к камере насоса и эксцентрично по отношению к колесу 6.

Между ступицей колеса, лопатками и внутренней гранью водяного кольца образуются полости, объем которых за первую половину оборота колеса, т. е. до вертикального диаметра, увеличивается. При увеличении объема полостей в них водокольцевого возникает разрежение и через серповидное отверстие (подводящее секторное отверстие 7) начинает поступать воздух.

П

Рис 2.25. Схема установки насоса

ри дальнейшем вращении колеса объем полости уменьшается, воздух сжимается и при достижении очередной полостью выходного серповидного отверстия а (нагнетательного отверстия 2) под действием избыточного давления выталкивается через напорный патрубок в атмосферу (или в трубопровод). Если всасывающий патрубок вакуум-насоса соединить с герметичной полостью, то в ней вследствие постоянного отсоса воздуха возникает вакуум.

В целях предотвращения перегрева воды в водяном кольце к вакуум-насосу подводят свежую воду, которая, непрерывно поступая в насос, замещает нагревшуюся.

Величина создаваемого насосом разряжения (вакуума) не может быть больше давления насыщенных паров поступающей в насос воды, поэтому понижение температуры воды ведет к повышению величины разряжения.

Основные параметры работы насосов и их характеристики. При выборе насосов необходимо, в первую очередь, руководствоваться условиями, определяющими работу насоса на практике – подачей, напором, мощностью, КПД, частотой вращения, высотой всасывания, и учитывать взаимосвязь этих параметров – характеристики насосов.

Напором H насоса называется приращение механической энергии, получаемое каждым ньютоном проходящей через насос жидкости, т. е. разность удельных энергий жидкости при выходе из насоса и при входе в него.

Это приращение происходит за счет энергии, получаемой насосом от электродвигателя. Напор измеряется в (Нм/Н), или в м. Удельная энергия жидкости при выходе из насоса (Рис 2.25).

,

и удельная энергия жидкости на входе в насос

,

, (2.5)

где Р_н, Z_н, υ_н – давление, расстояние от плоскости сравнения 0-0 до места установки манометра и скорость на выходе из насоса; Р_в, Z_в, υ_в – то же при входе в насос.

Так как диаметры всасывающего и напорного трубопроводов отличаются, как правило, незначительно, то величина третьего слагаемого в уравнении (2.5) обычно невелика.

Второе слагаемое (Z_н – Z_в) представляет собой расстояние по вертикали между манометром на напорной линии и вакуумметром на всасывающей линии установки и обычно не превышает 1 м.

Следовательно, напор действующего насоса может быть оценен по показаниям манометра Р_н и вакуумметра Р_в.

Полный напор насоса состоит из статического Н_ст и динамического Н_д

∙ (2.6)

Статическим напором насоса называется приращение удельной потенциальной энергии жидкости в насосе

. (2.7)

Динамическим напором насоса называется приращение удельной кинетической энергии жидкости в насосе

. (2.8)

Для определения теоретического напора динамического насоса рассмотрим движение жидкости в рабочем колесе центробежного насоса (Рис 2.26), состоящем из двух дисков: переднего и заднего с расположенными между ними лопастями, имеющими вид изогнутых цилиндрических поверхностей или поверхностей двойной кривизны. Лопасти рабочего колеса образуют каналы, по которым движется жидкость при вращении рабочего колеса. Рабочее колесо помещено в спиральную камеру (на Рис 2.26 не показана), которая служит для плавного отвода жидкости, поступающей в напорный трубопровод.

Жидкость подводится к рабочему колесу центробежного насоса аксиально, т. е. в направлении оси вала, со скоростью с₀. При входе в рабочее колесо жидкость меняет направление на радиальное и поступает в каналы рабочего колеса со скоростью с₁. На внешней окружности рабочего колеса ее скорость возрастает до с₂. В каналах рабочего колеса жидкость совершает сложное движение. Проходя через рабочее колесо, жидкость принимает участие во вращении вместе с колесом с окружной скоростью и и одновременно перемещается вдоль лопастей с относительной скоростью w.

А

Рис 2.27. К выводу основного уравнения динамических машин Эйлера

Рис 2.26. Движение жидкости в рабочем колесе центробежного насоса

бсолютная скорость движения жидкости равна геометрической сумме векторов окружной (переносной) скорости и относительной скорости :. Вектор окружной скорости w направлен по касательной к окружности, на которой расположена рассматриваемая точка, а вектор относительной скорости направлен по касательной к поверхности лопасти в той же точке.

Абсолютная скорость может быть также разложена на радиальную составляющую с_r (меридиональную скорость) и окружную составляющую с_и. При этом с_r = с∙sinα, с_и = с∙cos α, α – угол между вектором абсолютной скорости и касательной к окружности; β – угол между вектором относительной скорости и касательной к окружности.

Индекс 1 принят для обозначения скоростей жидкости на входе в рабочее колесо, индекс 2 – на выходе из него.

Зная величины с_2r u₂ и угол β₂, можно построить параллелограмм скоростей на выходе из рабочего колеса. Таким же способом при известных с_1r, u₁, β₁ может быть построен параллелограмм скоростей на входе в рабочее колесо (рис 2.26, 5.27).

Абсолютная скорость с₁ на входе определяется конструкцией подвода жидкости в насос. Большинство современных конструкций центробежных насосов имеет подвод жидкости в радиальном направлении. Тогда α₁ = 90 и cos α₁ = 0, следовательно, с_1u = 0. В этом случае устраняется удар набегающей лопасти рабочего колеса на поток жидкости, и поэтому уменьшаются потери энергии в рабочем колесе.

Для определения теоретического напора насоса воспользуемся теоремой об изменении моментов количества движения: изменение момента количества движения жидкости в единицу времени относительно оси вращения рабочего колеса центробежного насоса равно сумме моментов внешних сил относительно той же оси.

Мощность на валу насоса

, (2.9)

где М – момент внешних сил; ω – угловая скорость вращения вала рабочего колеса насоса.

Мощность, сообщаемая рабочим колесом потоку жидкости,

, (2.10)

где Q_m, Н_m – теоретическая подача и напор насоса.

При отсутствии потерь в насосе N₁= N₂ или , откуда теоретический напор насоса

. (2.11)

Масса жидкости, протекающей через рабочее колесо насоса m = ρQ_т, тогда момент количества движения жидкости относительно оси рабочего колеса на входе жидкости в рабочее колесо

, (2.12)

и на выходе из рабочего колеса

, (2.13)

где l₁ и l₂ – расстояния от оси колеса до входной и выходной скоростей (плечи приложения соответствующих моментов).

Согласно теореме об изменении моментов количества движения

.

Из рис 2.27 следует, что l₁=R₁ cos α₁, а l₂ = R₂ cos α₂, следовательно

, а

, (2.14)

где , – радиусы входного отверстия и рабочего колеса соответственно.

Но , , следовательно,

. (2.15)

Уравнение (2.15) называется основным уравнением динамических машин Эйлера.

Из рис. 2.27 следует, что c₂ cos α₂ = c_2u, c₁ cos α₂ = c_1u, тогда уравнение (2.15) можно представить в виде

. (2.16)

Если α₁ = 90 (рис 2.26), то cos α₁ = 0 и

. (2.17)

Основное уравнение динамических машин показывает, что теоретический напор, развиваемый насосом, тем больше, чем больше окружная скорость на внешней окружности рабочего колеса, т. е. чем больше его диаметр D₂, частота вращения n и угол β (см. рис 2.27), т. е. чем «круче» расположены лопасти рабочего колеса. Напор не зависит от рода перекачиваемой жидкости и, в частности, от ее плотности.

Напор, создаваемый объемными насосами, определяется конструкцией насоса, его прочностными характеристиками и мощностью электродвигателя, приводящего в движение рабочие органы насоса и не зависит от габаритных размеров и скорости движения рабочих органов насоса.

Подачей или производительностью насоса называется количество жидкости, подаваемое насосом в единицу времени в напорный трубопровод.

В зависимости от характера установки, обслуживаемой насосом, подача выражается в объемных, весовых или массовых единицах. Объемная подача Q измеряется в м³/с, м³/ч, л/мин и т. п. Весовая подача G измеряется в Н/с и т. п. Массовая подача измеряется в кг/с, т/ч и т. п. Объемная, весовая и массовая подачи связаны между собой соотношениями

, , (2.18)

где ρ – плотность перекачиваемой жидкости, кг/м³; g – ускорение свободного падения, м/с².

Для определения теоретической подачи центробежного насоса воспользуемся уравнением расхода

, (2.19)

где F – площадь поперечного сечения потока, м²; с_2r – средняя скорость жидкости, нормальная к этому сечению, м/с.

Площадь живого сечения потока на выходе из рабочего колеса центробежного насоса без учета стеснения его лопастями определим как боковую поверхность цилиндра диаметром, равным диаметру колеса D₂, и высотой, равной ширине канала колеса b₂ (рис 2.26), т. е. F = πD₂b₂. Скорость потока, нормальная этой поверхности, меридиональная скорость с_2r = с sin α₂. Подставляя полученные значения F и с_2r в уравнение расхода (2.20), получим формулу для определения теоретической подачи насоса

. (2.20)

С учетом стеснения потока лопастями рабочего колеса

, (2.21)

где ψ – коэффициент стеснения.

Теоретическая (идеальная ) подача объемного насоса

, (2.22)

где V₀ – рабочий объем насоса, т. е. подача насоса за один цикл (один оборот вала насоса); п – частота рабочих циклов насоса (для вращательных насосов частота вращения вала); V_k – теоретическая подача из каждой рабочей камеры за один цикл; z – число рабочих камер в насосе; k – кратность действия насоса, т. е. число подач из каждой камеры за один рабочий цикл (один оборот вала).

Энергия, получаемая насосом от электродвигателя в единицу времени, представляет собой потребляемую насосом мощность, или мощность на валу насоса, которую обозначим через N_l. Часть этой энергии теряется в насосе. Если вычесть из потребляемой мощности N_l. мощность всех потерь ∆N в насосе, то получим полезную мощность насоса N_п = N_l - ∆N. Полезная мощность N_п представляет собой приращение энергии всей жидкости G в насосе в единицу времени

, (2.23)

где Q – подача насоса, м³/с; Н – напор насоса перекачиваемой среды, м; ρ – плотность перекачиваемой жидкости, кг/м³.

Действительные подача Q и напор Н, используемые в формуле (2.23), отличаются от теоретических подачи Q_т и напора Н_т, рассчитываемых по формулам (2.20 – 5.22) и (2.15 – 5.17) соответственно. Действительные подача и напор меньше теоретических вследствие всевозможных потерь в насосе.

Потери энергии в насосе характеризуются полным КПД насоса η_п, представляющим собой отношение .

О

Рис 2.28. Схема к определению высоты всасывания насоса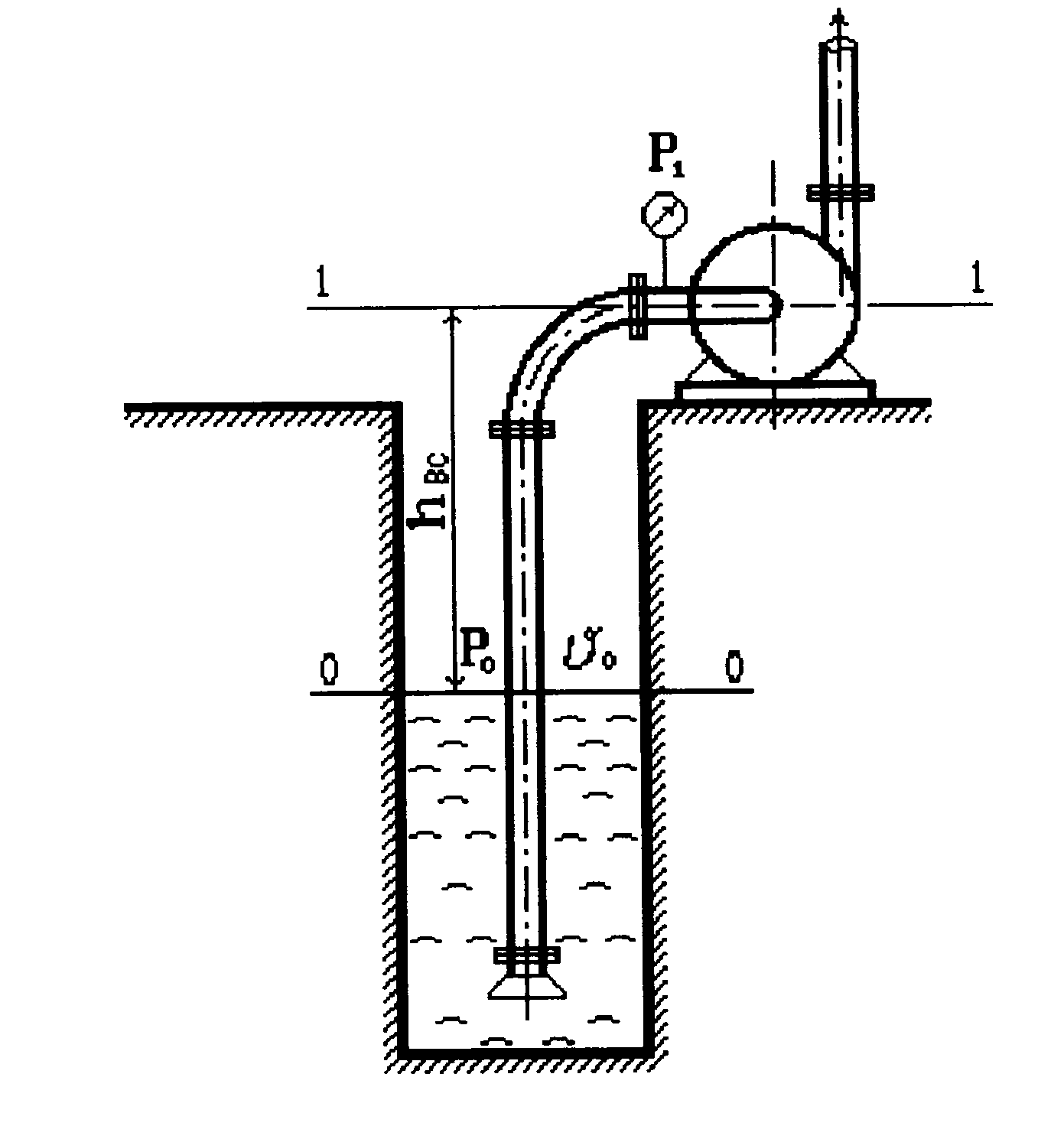

тсюда потребляемая насосом мощность (в кВт)

. (2.24)

Полный КПД насоса равен произведению объемного, гидравлического и механического КПД η_п=η_оη_гη_м и характеризует степень совершенства конструкции насоса. Полный КПД центробежных насосов лежит в пределах 0,75…0,92.

Назначение или выбор числа оборотов зависит от ряда условий, из которых наиболее важным является тип насоса и двигателя, допустимая высота всасывания, степень экономичности, весовые и габаритные показатели.

Всасывание жидкости насосом происходит за счет разности давлений на свободной поверхности жидкости в источнике и у входа в рабочее колесо (рис 2.28). Давление в потоке у входа в колесо зависит от расположения уровня поверхности жидкости в источнике (резервуаре) и режима работы насоса. Эта разность давлений равна величине вакуума, или вакуумметрической высоте всасывания Н_вак, измеряемой в метрах столба перекачиваемой жидкости вакуумметром . Поскольку лопастные насосы не являются самовсасывающими, то для создания в нем разрежения их перед пуском необходимо залить перекачиваемой жидкостью (вместе со всасывающим трубопроводом). Разность отметок оси горизонтального насоса и уровня жидкости в источнике (приемном резервуаре) называется геометрической высотой всасывания насоса h_вс. Для определения высоты всасывания насоса составим уравнение Бернулли для двух сечений 0-0 и 1-1, проведенных по уровню свободной поверхности жидкости в резервуаре и по оси рабочего колеса насоса соответственно. Сечение 0-0 примем за плоскость сравнения. Тогда

. (2.25)

В виду того, что скорость в источнике невелика (т. к. объем жидкости в нем велик), величиной можно пренебречь. Тогда геометрическая высота всасывания

. (2.26)

где h_п.вс – потери напора во всасывающем трубопроводе, м.

Как видно, высота всасывания тем больше, чем меньше давление в насосе, скоростной напор во всасывающем трубопроводе и потери напора в нём.

Из уравнения (2.25)

. (2.27)

Таким образом, давление у входа в насос и, следовательно, в рабочем колесе насоса тем меньше, чем больше высота всасывания, гидравлическое сопротивление и скорость во всасывающем трубопроводе и чем меньше давление в приёмном резервуаре. Нормальная работа центробежного насоса обеспечивается в таком режиме, когда абсолютное давление во всех точках его внутренней полости больше давления насыщенных паров перекачиваемой жидкости при данной температуре. Если такое условие не соблюдается, то начинается явление кавитации, приводящее к уменьшению или даже прекращению подачи насоса.

Возникновение и характер кавитационных явлений определяются кавитационным запасом – превышением удельной энергии жидкости при входе в насос над удельной энергией ее насыщенных паров

, (2.28)

г

Рис 2.29. Рабочая характеристика насоса

де Р₁, Р_н – абсолютное давление жидкости на входе в насос и ее насыщенных паров при данной температуре; – скорость жидкости на входе в насос.

Рассмотренные выше параметры работы насосов находятся между собой во взаимосвязи, причем эта связь может иметь различный характер для различных насосов. Взаимосвязь различных параметров работы насоса называется характеристикой насоса.

Рассмотрим рабочую характеристику динамических насосов (рис 2.29), имеющую важное значение для практических расчетов.

Рабочая характеристика насоса – это графическая зависимость основных параметров Н, N, η от подачи Q при постоянной частоте вращения, вязкости и плотности перекачиваемой среды на входе в насос. Характеристика насоса позволяет определить подачу насоса при заданном полезном сопротивлении по кривой Q-H и затраты энергии – по кривой Q-N.

Кривая Q-η служит для оценки экономичности действия насоса, и ее легко построить из первых двух простым расчетом.

Максимум кривой Q-η соответствует оптимальному режиму. Значения подачи, напора, мощности и КПД, приведенные в справочниках, обычно относятся именно к этому режиму. Зона, в пределах которой рекомендуется эксплуатация насоса, называется рабочей частью характеристики и определяется, как правило, зоной снижения КПД на 2…3 % от максимального его значения. Мощность холостого хода N₀ при Q = 0 и вид кривой N = f(Q) зависят от типа насоса. Полезная мощность при Q = 0 равна нулю, поэтому и КПД насоса равен нулю.

Поле характеристик насосов (сводный график полей насосов) строится в логарифмических координатах и охватывает требуемый диапазон параметров Q и Н (рис 2.30) для выбранного типа насосов.

Рис 2.30. Поле Q-H насосов центробежных консольных общего назначения для воды

Требуемый диапазон Q-Н стремятся покрыть минимальным числом типоразмеров насосов. Основные параметры насосов (Q, H) берут в соответствии с рядом предпочтительных чисел: границы Q и Н для каждого насоса предусматривают его работу в зоне оптимальных режимов по КПД, всасывающей способности и т. д. Такие графики прилагаются к каталогам насосов, выпускаемых промышленностью, и облегчают выбор насоса (по заданным значениям подачи и напора находят на сводном графике режимную точку и соответствующую ей марку и частоту вращения насоса).

В

Рис 2.31. Схема насосной установки:

1 – фильтр; 2 – обратный клапан;

3 – всасывающий трубопровод;

4 – электродвигатель; 5 – насос;

6 – задвижка; 7 – напорный трубопровод; 8 – моновакуумметр;

9 – манометр; 10 – расходомер

ыбор насоса, работающего на сеть. Рабочая точка насоса. В соответствии со своим основным назначением насос работает в совокупности с системой трубопроводов, включающих в себя различные аппараты, образующий насосную установку (рис 2.31).

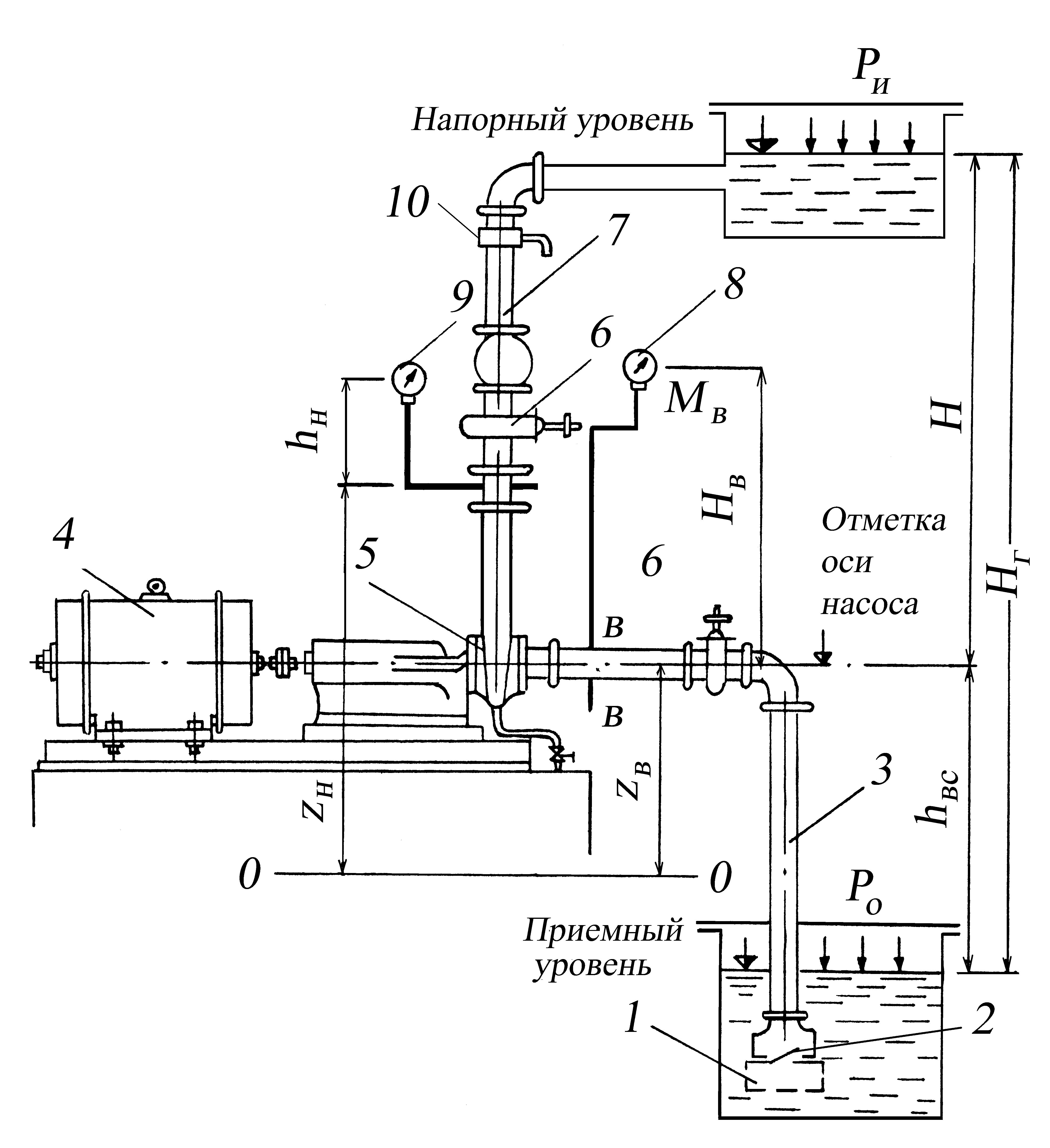
К насосу 5, приводимому от электродвигателя 4, жидкость поступает из приемного резервуара (источника) по всасывающему трубопроводу 3, оборудованному фильтром 1 и обратным клапаном 2. Насос нагнетает жидкость в напорный бак (резервуар) по напорному трубопроводу 7. На напорном трубопроводе устанавливается задвижка 6, при помощи которой регулируется подача насоса. Работа насоса контролируется по расходомеру 10, который измеряет подачу насоса по манометру 9 и моновакуумметру 8, дающими возможность определить напор насоса.

Для того чтобы перемещать жидкость по трубопроводам установки из приемного резервуара в напорный, необходимо затрачивать энергию на подъем жидкости на высоту Н_Г=Н+h_вс, на преодоление разности давлений Р_н-Р₀ в резервуарах и на преодоление гидравлических сопротивлений Σh_п в трубопроводах, соединяющих эти резервуары. Таким образом, энергия, необходимая для перемещения единицы веса жидкости (Н) из приемного резервуара в напорный по трубопроводам установки, определяется по уравнению

, (2.29)

где – статический напор насосной установки.

Поскольку статический напор установки от расхода не зависит, а насосные установки, как правило, эксплуатируются при турбулентном режиме, где потери напора (сопротивление) пропорциональны квадрату скорости, а следовательно, и подаче Σh_п = bQ², то уравнение (2.23) может быть преобразовано к виду

, (2.30)

где b – коэффициент пропорциональности, зависящий от условий эксплуатации трубопроводов насосной установки.

Уравнение (2.30) называется характеристикой насосной установки или характеристикой сети. На Рис 2.32 справа изображена схема насосной установки, слева – характеристика сети СЕ, представляющая собой ветвь параболы Σh_п = bQ² с вершиной в точке С, отсекающей на оси ординат отрезок .

З

Рис 2.32. Совмещенные характеристики насоса и трубопровода

десь же изображена характеристика насоса Q-Н, работающего на сеть. Точка А пересечения характеристик сети и насоса называется рабочей точкой насоса. Подача Q_А, соответствующая рабочей точке насоса, определяет собой количество жидкости, подаваемой насосом в напорный трубопровод. Если подача Q_А не равна заданной (требуемой) подаче, например, Q_В (Рис 2.32), то необходимо отрегулировать работу насоса на сеть.

Р

Рис 2.33. Определение режима работы нерегулируемого (а) и регулируемого (б) насосов на гидросеть

ассмотрим работу объемного насоса на сеть. Для определения режима работы насоса и сети следует совместить на одном чертеже в одинаковом масштабе характеристики насоса 2 и сети 3. Точка пересечения характеристик – точка А (рабочая точка) определит режим работы насоса: давление Р_А и подачу Q_А при работе с данной сетью, характеристика которой Р_пот=Р_ст+∆Р_Г или Р_потТ=Р_ст+SQ² (кривая 3 Рис 2.33, а). Для уменьшения подачи до Q_А1 необходимо, чтобы характеристика сети прошла через рабочую точку А₁ (кривая 3^’) с координатами Q_А1 и Р_А1. Это станет возможным, если увеличить сопротивление сети с помощью дросселя на ∆Р_ДР= Р_А1-(Р_СТ+∆Р_Г). В сеть поступит только часть подачи насоса Q_н(Q_с =Q_А1), остальная часть Q_кл возвращается через клапан в бак, не выполнив полезной работы. Мощность насоса остается той же, что и до дросселирования.