
ЛЕКЦИЯ 2-1
ЛЕКЦИЯ 2
ТЕМА:
1. Линии. Определение, задание на чертеже. Прямая.
2. Положение прямой относительно плоскостей проекций.
3. Следы прямой.
4. Взаимное положение линий, точки и линии. Определение
видимости на чертеже.
5. Определение длины отрезка прямой.
6. Деление отрезка прямой в заданном отношении.
7. Задание на чертеже окружности. Ортогональные проекции винтовой линии.
1.Линии.
Линии в зависимости от формы и способа образования делятся на прямые и кривые линии, на плоские и пространственные.
Прямая линия – кратчайшее расстояние между двумя точками.
Кривая линия – след точки, движущейся по определенному закону; или другое определение – геометрическое место точек, обладающих данными свойствами. Кривые линии могут быть заданы аналитически, то есть уравнениями, и графически на чертеже.
Порядок плоской кривой геометрически определяется так: порядком называется число точек пересечения кривой с прямой линией.
Плоские линии – все точки, которой принадлежат одной плоскости.
Пространственные – не лежат всеми своими точками в одной плоскости. Порядок пространственной кривой называется число ее точек пересечения с плоскостью общего положения.
Две точки определяют положение прямой в пространстве, поэтому чтобы задать прямую на чертеже необходимо иметь не менее двух проекций двух точек, принадлежащих данной прямой, и соединить их одноименные проекции.
Образование прямой аналогично образованию комплексного чертежа точки. Прямую прямоугольно проецируют на две взаимно перпендикулярные плоскости проекций П1 и П2 (рис.1). Плоскость П1 вращением вниз вокруг оси ох совмещают с плоскостью П2 и получают эпюр двух проекций А'В' и А''В'' (рис.2). Для построения третьей проекции прямой достаточно построить третьи проекции точек, ее задающих и соединить их прямой или, имея безосный эпюр, более предпочтительный способ построения третьей проекции на рис.5.
ЛЕКЦИЯ 2 –2


 П2
П2


 А″
А″





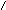
 A
А″ Аz
А′″
A
А″ Аz
А′″ 


 B″
B
B″
B″
B
B″ 






 B′″
B′″
 Ax
Ax




 Bх
A′ Bх
Аx
0
Bх
A′ Bх
Аx
0

B′



 П1
B′
А′ Ау
П1
B′
А′ Ау

Рис. 1 Рис. 2
2.Положение прямой относительно плоскостей проекций
На рисунках 1,2,3,4 и 5 заданы прямые общего положения, т.е. не параллельные и не перпендикулярные ни одной из плоскостей проекций.






 А''
А'' А'''
А''
А'' А'''

 А''
А''






 В''
В''
В'' В'''
В''
В''
В'' В'''

 х
х
х
х


 В'
В'
А'
В'
В'
А'
 А'
А' В'
А'
А' В'
Рис. 3 Рис. 4 Рис. 5
Прямые частного положения.
Прямые по отношению к плоскостям проекций могут быть параллельны и называться линиями уровня: горизонталь h – прямая, параллельная горизонтальной плоскости проекций П1 (рис.6 и 7). Запомнить: h// П1 h''//ox h' – по построению.


 П2
П2















 h''
h
h''
h'''
h''
h
h''
h'''









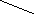









 h'
h'
 П1
h'
П1
h'
Рис. 6 Рис. 7
ЛЕКЦИЯ 2 - 3
Фронталь – прямая, параллельная фронтальной плоскости проекций П2 (рис. 8 и 9).
f // П2 f' // ox f'' – строится по построению









 f′′
f
f′′
f′′
f
f′′


 П1
П1








 f′ f′
f′ f′
 П2
П2
Рис.8 Рис.9
Профильная прямая – прямая, параллельная профильной плоскости проекций П3.
p//П3 p'//p''//ox и p''' по построению
П


 роецирующие
прямые – перпендикулярные одной из
плоскостей проекций (соответственно
параллельные двум другим). Проецирующая
прямая отображается точкой на плоскость,
которой она перпендикулярна, которая
называется следом этой прямой. На
других плоскостях проекций отображаются
прямыми перпендикулярными оси проекций.
Смотри рис.10 и рис.11.
a′′
роецирующие
прямые – перпендикулярные одной из
плоскостей проекций (соответственно
параллельные двум другим). Проецирующая
прямая отображается точкой на плоскость,
которой она перпендикулярна, которая
называется следом этой прямой. На
других плоскостях проекций отображаются
прямыми перпендикулярными оси проекций.
Смотри рис.10 и рис.11.
a′′
П1





 а′′
а b′′
а′′
а b′′





 b′′
x
b′′
x


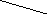


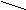 b
a′
b′ a′
b
a′
b′ a′
 b′ П2
b′ П2
Рис. 11 Рис. 10
