5. Теорема об изменении кинетической энергии системы при ударе. Теорема Кельвина

Получим выражение для работы ударных сил. Умножив скалярно члены уравнения (7.1) на U и V, получим

Сложив эти уравнения и разделив на 2, находим

То есть изменение кинетической энергии точки при ударе равно работе А ударной силы F.

Теорема Кельвина:

(10.11)

Работа ударной силы, приложенной к точке, за время удара равна скалярному произведению ударного импульса на полусумму скоростей точки после и до удара.

Выведем теорему об изменении кинетической энергии при ударе для материальной точки. При падении материальной точки на гладкую поверхность происходит наложение идеальной стационарной неупругой связи. В начале фазы деформирования скорость точки равна V, а в конце U₁ = U_. Импульс в фазе деформирования S₁. Так как ударная поверхность гладкая, . Запишем для фазы деформирования уравнения, выражающие теорему Кельвина и теорему об изменении количества движения

Умножив второе уравнение скалярно на S₁, получим

Окончательно имеем

(10.12)

При мгновенном наложении связи на точку происходит потеря её кинетической энергии. Для фазы восстановления скорости точки в начале и в конце фазы будут соответственно U₁ иU, импульс ударной реакции S₂. Так как S₂ U₁, то .

Далее аналогично записываем

Умножив второе уравнение скалярно на S₂, получим

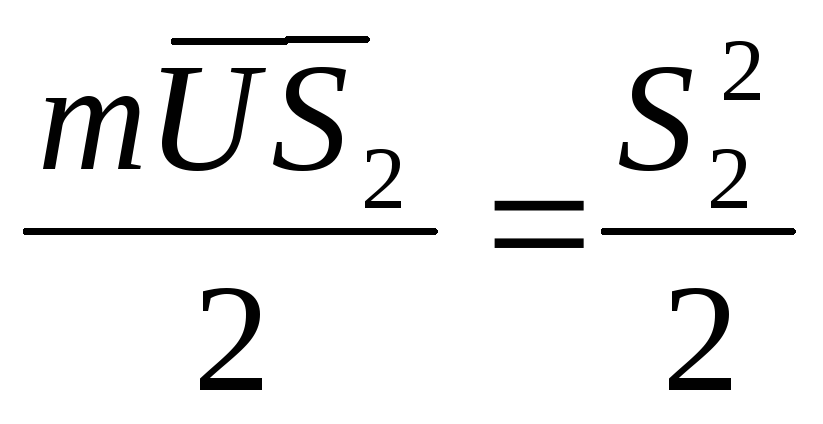
Окончательно имеем

(10.13)

В фазе восстановления происходит мгновенное снятие связи. При этом изменение кинетической энергии точки положительное.

Сложив (7.10) и (7.11), получим

Кроме того, Отсюда

Окончательно получим

так как , то

(10.14)

Величину называют потерянной скоростью точки, а

– кинетической энергией точки, соответствующей потерянной скорости.

Из уравнения (7.12) следует, что в результате удара при происходит потеря кинетической энергии точки, а при k = 1 (при абсолютно упругом ударе) потери кинетической энергии отсутствуют.

Проведя аналогичные выводы для механической системы, будем иметь:

Обозначим кинетическую энергию системы, соответствующую потерянным скоростям точек, через Т_пс, тогда

(10.15)

Теорема Карно

Потеря кинетической энергии системы при упругом ударе в случае мгновенного наложения идеальных связей равна кинетической энергии системы, которая соответствует потерянным скоростям точек системы, умноженной на коэффициент .