2. Теоремы об изменении количества движения и о движении центра масс системы при ударе

Теорема об изменении количества движения точки при ударе для i-й точки механической системы

(10.3)

Суммируя уравнения (7.3) по точкам системы, получаем

(10.4)

Но как было показано ранее . Используя понятие главного вектора количеств движения механической системы перепишем уравнение (7.4)

(10.5)

Теорема об изменении количества движения системы при ударе

Изменение количества движения механической системы за время удара равно векторной сумме импульсов всех внешних ударных сил, действующих на точки системы.

Используя известное выражение для главного вектора количеств движения механической системы , перепишем уравнение (10.5)

(10.6)

Уравнение (7.6) выражает теорему об изменении количества движения центра масс системы при ударе.

Изменение за время удара количества движения центра масс системы, в котором сосредоточена вся её масса, равно геометрической сумме всех внешних ударных импульсов, действующих на эту систему.

То есть внутренние ударные импульсы, возникающие, например, при столкновении тел, входящих в состав данной системы, не изменяют скорости центра масс этой системы.

3. Теорема об изменении главного момента количеств движения системы при ударе

Запишем снова основное уравнение теории удара для i-й точки механической системы

(10.3)

Обозначим радиус-вектор i-й точки системы относительно начала неподвижной инерциальной системе отсчёта через r_i. Так как перемещение i-й точки системы за время удара пренебрежимо мало и его можно не учитывать, то за время удара не изменяется и её радиус-вектор r_i.

Умножим обе части уравнения (7.3) векторно слева на радиус-вектор r_i и просуммируем это уравнение по индексу i для всех точек системы.

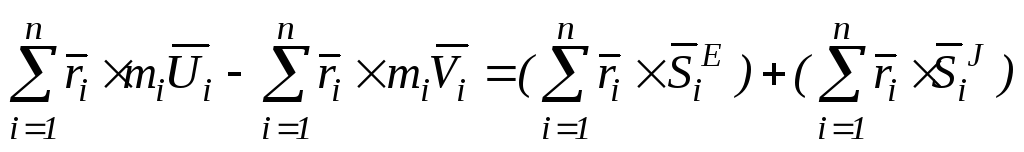
Обозначим: 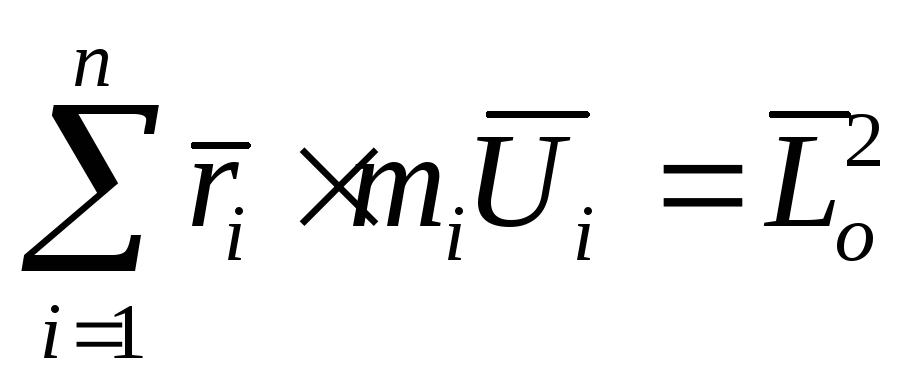- главный момент количеств движения системы относительно т. О после удара.

- аналогично главный момент количеств движения системы относительно т. О до удара.

- главный момент всех внешних ударных импульсов, приложенных к точкам системы, относительно центра О.

- главный момент всех внутренних ударных импульсов, приложенных к точкам системы, относительно центра О. (по свойству внутренних сил системы равен нулю).

Подставляем эти значения в полученное уравнение

(10.7)

Уравнение (7.4) выражает теорему об изменении главного момента количеств движения системы при ударе:

Изменение главного момента количеств движения системы относительно какой-либо точки за время удара равно векторной сумме моментов импульсов внешних ударных сил, приложенных к материальным точкам системы? относительно той же точки.

Таким образом, если , то , то есть внутренние ударные импульсы не могут изменить кинетического момента системы (закон сохранения).

4. Коэффициент восстановления

(10.8)

где - импульсы ударных сил в фазах деформирования и восстановления для первого и второго тел соответственно.

Пусть материальная точка массой m падает на гладкую поверхность со скоростью V, направленной под углом к нормали к поверхности. После удара скорость точки U составит с нормалью угол , угол – угол падения, угол  - угол отражения. Если - удар косой, если удар прямой. Импульс S ударной реакции поверхности направлен по нормали к поверхности.

Для определения коэффициента восстановления k представим удар точки о поверхность в двух фазах где 1, N – время фазы деформирования и нормальная ударная реакция поверхности. В конце фазы деформирования U1 = U Импульс ударной реакции во второй фазе . Коэффициент восстановления для точки (10.9) - для прямого удара ; (7.7) - для косого удара (10.10)