ЛЕКЦИИ ТЕОРМЕХ / Лек14Д(през)

ЛЕКЦИЯ 14Д

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В ОБОБЩЁННЫХ КООРДИНАТАХ

1. Уравнения Лагранжа 2-го рода

2. Кинетический потенциал

3. Циклические координаты

1. Уравнения Лагранжа 2-го рода

Общее уравнение динамики в обобщённых координатах выглядит следующим образом:

, (14.1)

где

- обобщённая активная сила

- обобщённая сила инерции

Выберем обобщённые координаты (где S – число степеней свободы) и выразим декартовы координаты точек системы через эти обобщённые координаты

(14.2)

для всех .

Учитывая, что

Радиус-вектор точки М_i также является функцией обобщенных координат и времени

(14.3)

Так как обобщённые координаты системы являются функциями времени, то радиус-вектор r_i является сложной функцией времени и вектор скорости точки V_i определяется по правилу дифференцирования сложной функции

(а)

или

(14.4)

а в случае стационарных связей

(14.5)

Здесь производные от обобщённых координат по времени представляют собой обобщённые скорости.

Из выражения (а) следует, что частная производная от V_i по какой-либо обобщённой скорости равна коэффициенту при

- первое тождество Лагранжа (б)

Кинетическая энергия механической системы определяется по формуле

(14.6)

Из выражения (14.4) следует

Найдём частные производные кинетической энергии по обобщённой координате и обобщённой скорости , дифференцируя уравнение (14.6) как сложную функцию обобщенных координат и обобщенных скоростей

Преобразуем последнее выражение на основании равенства (б)

Продифференцируем это выражение по времени

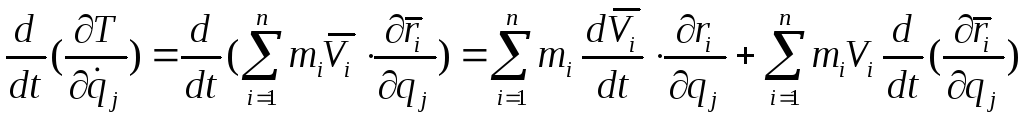(в)

Рассмотрим обе суммы, входящие в правую часть равенства (в).

Для несвободной материальной точки

1. На основе выражения для обобщённой силы, находим:

2. Для установления значения второй суммы рассмотрим выражение

(г)

Найдём частную производную (, дифференцируя по выражение (а)

(д)

- второе тождество Лагранжа

Пользуясь этой зависимостью, преобразуем вторую сумму в правой части равенства (в)

Подставляем найденные значения обеих сумм в равенство (в) и рассматриваем механическую систему со стационарными идеальными связями, для которых

или

(14.7)

Последовательность действий

при использовании уравнений Лагранжа второго рода:

1. Определить число степеней свободы системы и выбрать наиболее удобные обобщённые координаты;

2. Вычислить кинетическую энергию системы и выразить её через обобщённые координаты и обобщённые скорости;

3. Вычислить производные от кинетической энергии;

4. Определить обобщённые силы, соответствующие выбранным обобщённым координатам;

5. Подставить все вычисленные величины в уравнения Лагранжа и определить искомую величину (чаще всего это - ускорение).

Для составления левых частей этих уравнений следует выразить кинетическую энергию через обобщённые координаты и обобщённые скорости.

Обобщённые силы могут быть найдены либо непосредственно, через проекции на оси декартовых координат (уравнение (13.6)),

либо как координаты при вариациях обобщённых координат в выражении для возможной работы (уравнение (13.4)).

2. Кинетический потенциал

Если на рассматриваемую систему действуют только консервативные силы, то обобщённая сила определяется

В этом случае уравнения Лагранжа второго рода принимают следующий вид

L = Т – П - функция Лагранжа или кинетический потенциал

Так как

и

Следовательно, кинетический потенциал L является функцией обобщённых координат, обобщённых скоростей и времени

Потенциальная энергия является функцией только обобщённых координат и времени, поэтому

Пользуясь этим условием, получим

Т = L + П,

Подставив эти частные производные в уравнения Лагранжа, получим

(14.8)

Уравнения (14.8) называют уравнениями Лагранжа второго рода для консервативной системы.

3. Циклические координаты

Обобщённые координаты, которые не входят явно в выражение кинетического потенциала L, называются циклическими координатами.

Предположим, что среди S обобщённых координат системы координаты являются циклическими.

Тогда по определению циклических координат производные от кинетического потенциала по этим координатам равны нулю:

(14.9)

В этом случае k уравнений (14.9) принимают вид

откуда

Эти уравнения называются циклическими интегралами.

Примеры:

1) Положение точки в пространстве определяется тремя координатами. Примем декартовы координаты за обобщённые. Тогда

Кинетический потенциал точки

Координаты x, y не входят в выражении кинетического потенциала L, то есть являются циклическими координатами. Циклические интегралы имеют вид

или

или

Эти выражения показывают, что проекции скорости точки на горизонтальные оси координат постоянны, то есть под действием силы тяжести изменяется только вертикальная составляющая скорости точки.