ЛЕКЦИИ ТЕОРМЕХ / Лек2Д(през)

ТЕМА: ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ

Лекция 2Д

ВВЕДЕНИЕ В ДИНАМИКУ МЕХАНИЧЕСКОЙ СИСТЕМЫ

1. Механическая система. Силы внешние и внутренние. Классификация связей.

2. Дифференциальные уравнения движения механической системы.

3. Центр масс механической системы.

4. Теорема о движении центра масс.

1. Механическая система. Силы внешние и внутренние.

Классификация связей.

Система материальных точек (механическая система) - это такая совокупность точек, в которой положения или движения каждой точки зависит от положения и движения всех остальных.
Система свободных точек - это такая система материальных точек, движение которых не ограничено никакими связями, а определяется лишь действующими на эти точки силами (пример – солнечная система).	Система несвободных точек – это система материальных точек, движения которых ограничиваются наложенными на точки связями (пример - любой механизм или машина, у которых движения отдельных элементов ограничены связями).

Классификация сил

Задаваемые (активные) силы Реакции связей
Внешние силы Внутренние силы

1. Главный вектор всех внутренних сил системы и суммы их проекций на координатные оси равны нулю:

(2.1)

(2.2)

2. Главные моменты всех внутренних сил системы относительно любого центра и координатных осей равны нулю:

(2.3)

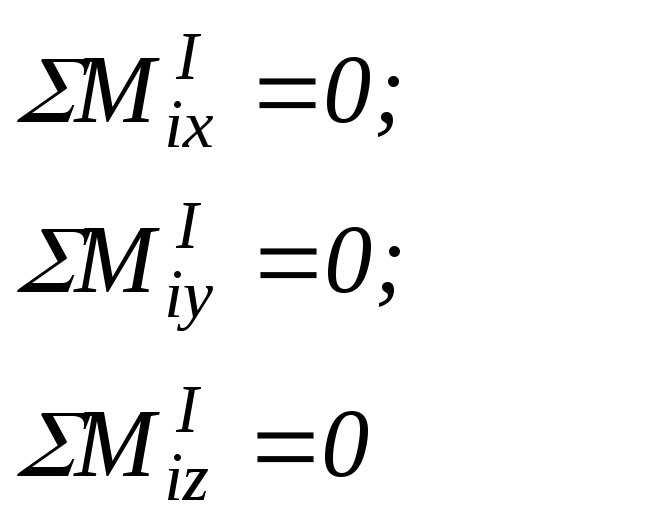
(2.4)

Хотя уравнения (2.1) - (2.4) имеют вид уравнений равновесий сил, произвольно расположенных в пространстве, внутренние силы не уравновешиваются, так как они приложены к различным точкам системы и могут вызывать перемещения этих точек относительно друг друга.

Классификация связей

1-я классификация

Связи
Двусторонние (удерживающие)			Односторонние (неудерживающие)
Конечные	Дифференциальные
	Интегрируемые	Неинтегрируемые
Голономные		Неголономные

2-я классификация

Связи
Стационарные	Нестационарные

Пример двусторонней, голономной, стационарной связи – абсолютно жёсткий стержень.

Пример нестационарной связи

2. Дифференциальные уравнения движения механической системы.

Основное уравнение динамики для материальной точки Mi (): (2.5) (2.6)

где - внешняя сила, действующая на точку M_i;

- внутренняя сила, действующая на точку M_i;

,, - проекции силы на оси координат;

, , - проекции силы на оси координат.

3. Цент масс механической системы

Центром масс или центром инерции механической системы называется воображаемая точка, которая как бы обладает массой, равной массе всей системы, и положение которой определяется радиусом-вектором: (2.7) где m=mi – масса системы.

(2.8)

Центр тяжести тела или системы тел является центром масс этой системы.

4. Теорема о движении центра масс механической системы.

Закон сохранения движения центра масс

Положение центра масс системы С определяется равенством (2.7)

Уравнения движения точек этой системы имеют вид:

Суммируем эти уравнения:

(а)

Преобразуем левую часть равенства учитывая (2.7)

Ранее мы показали, что геометрическая сумма внутренних сил равна нулю, тогда уравнение (а) приобретает вид

или (2.9)

т.е произведение массы системы на ускорение её центра масс равно геометрической сумме всех действующих на систему внешних сил или главному вектору этих сил.

Теорема о движении центра масс

Центр масс механической системы движется как материальная точка массой, равной массе всей системы, к которой приложены все внешние силы, действующие на систему.

Проектируя обе части векторного равенства (15.9) на оси X, Y, Z получаем три уравнения в проекциях на оси координат

(2.10)

Где X_i^E, Y_i^E, Z_i^E проекция силы ;

- проекции главного вектора внешних сил на оси координат.

Следствия из теоремы.

1. Если главный вектор внешних сил остаётся всё время равным нулю, то центр масс механической системы находится в покое или движется прямолинейно и равномерно.

2. Если проекция главного вектора внешних сил на какую-либо неподвижную ось остаётся всё время равной нулю, то проекция центра масс механической системы на эту ось или неподвижна или движется равномерно.