ЛЕКЦИИ ТЕОРМЕХ / Лек12Д(през)

ЛЕКЦИЯ 12Д

ПРИНЦИП ВОЗМОЖНЫХ ПЕРЕМЕЩЕНИЙ.

ОБЩЕЕ УРАВНЕНИЕ ДИНАМИКИ.

1. Возможные перемещения точки и системы.

2. Идеальные связи.

3. Принцип возможных перемещений.

4. Общее уравнение динамики.

1. Возможные перемещения точки и системы

Возможные перемещения точек системы должны удовлетворять двум условиям:

1) они должны быть бесконечно малыми, так как при конечных перемещениях система перейдёт в другое положение, где условия равновесия могут быть другими;

2) они должны быть такими, чтобы все наложенные на систему связи сохранились, так как иначе мы изменим вид рассматриваемой механической системы (система станет другой).

Пример перемещений, которые не являются возможными

Возможные перемещения рассматривают как величины первого порядка малости, пренебрегая при этом величинам высших порядков малости. Поэтому криволинейные перемещения точек заменяют прямолинейными отрезками, отложенными оп касательным к траекториям точек и обозначают .

Возможные перемещения точек кривошипно-шатунного механизма

Таким образом, возможным перемещением системы будем называть любую совокупность бесконечно малых перемещений точек системы, допускаемых в данный момент всеми наложенными на систему связями.

Уравнения связей

2. Идеальные связи

Наложенные на систему связи являются идеальными, если сумма элементарных работ реакций этих связей на любом возможном перемещении системы равна нулю.

- теорема об изменении кинетической энергии механической системы.

- разделим все силы, действующие на механическую систему на активные силы и реакции связей.

3. Принцип возможных перемещений

Рассмотрим систему материальных точек, которая под действием всех приложенных к ней сил и наложенных на неё связей находится в равновесии.

- равнодействующая всех приложенных к точке М_i системы активных (внешних и внутренних) сил.

- равнодействующая всех реакций связей, приложенных к точке М_i системы.

Так как точка М_i вместе со всей системой находится в равновесии, то

или .

(12.1)

где - возможная работа активных сил, приложенных к точке М_i системы;

- возможная работа реакций связей, приложенных к точке М_i системы.

Для всей системы

(12.2)

Если наложенные на систему связи являются идеальными, то , следовательно

или (12.3)

Доказана необходимость принципа.

Докажем достаточность принципа способом от противного:

, что противоречит (12.3). Отсюда вытекает принцип возможных перемещений.

Для равновесия механической системы с двусторонними идеальными связями необходимо и достаточно чтобы сумма элементарных работ всех действующих на неё активных сил на любом возможном перемещении системы была равна нулю.

Если смещение точек системы из положения равновесия происходит за малый промежуток времени  , то возможные скорости точек этой системы можно определить:

и т.д.

Направление возможных скоростей, очевидно, совпадает с направлением возможных перемещений.

4. Общее уравнение динамики

Для точки М_i несвободной механической системы принцип Даламбера имеет вид

,

где равнодействующая активных сил, приложенных к материальной точке;

равнодействующая реакций связей, приложенных к материальной точке;

сила инерции материальной точки.

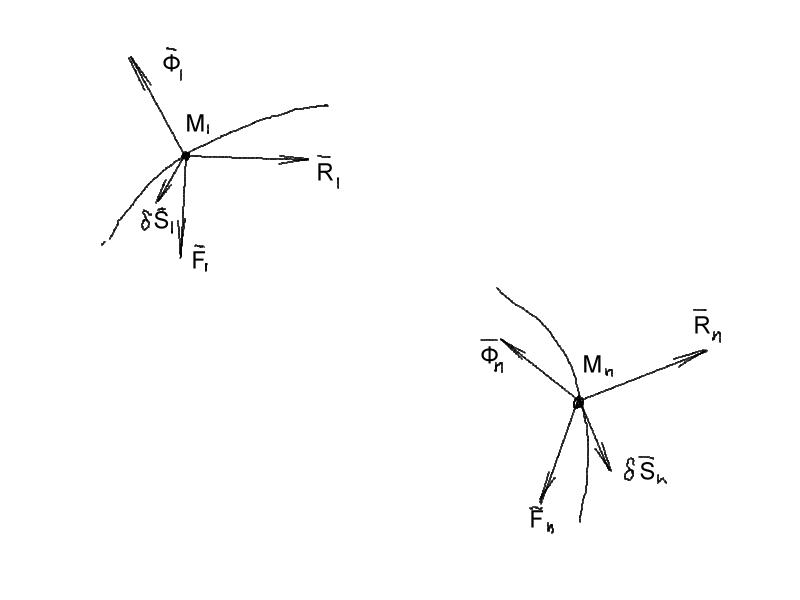
Если система получает возможное перемещение, при котором каждая точка имеет возможное перемещение S_i , то сумма работ этих сил на перемещении S_i должна быть равна нулю.

(12.4)

Для n материальных точек механической системы:

(12.5)

Положим, что все связи в рассматриваемой системе идеальные, тогда

Тогда уравнение (12.5) примет вид:

(12.6)

Уравнение (12.6) - общее уравнение динамики, показывает, что

В любой момент времени сумма работ всех задаваемых сил и сил инерции материальных точек несвободной механической системы с двусторонними идеальными связями на любом возможном перемещении равна нулю.

Если в каждую точку M_i системы из некоторого центра О провести вектор r_i, то возможное перемещение этой точки S_i будет соответствующим приращением радиуса-вектора точки:

(i = 1,n)

Тогда работу задаваемых сил и сил инерции можно представить в виде скалярных произведений сил на возможных перемещениях точек системы:

;

или

(12.7)

Если - проекции активной силы Р_i,

- проекции силы инерции Ф_i,

- проекции приращения радиуса-вектора , то

Выразим:

Получим:

(12.8)

Общее уравнение динамики (12.8) позволяет составить дифференциальные уравнения движения любой механической системы.