ЛЕКЦИИ ТЕОРМЕХ / Лек11Дпрез)
.docЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
ЛЕКЦИЯ 11Д
ПРИНЦИП ДАЛАМБЕРА
-
Сила инерции материальной точки.
-
Принцип Даламбера для материальной точки и механической системы.
-
Приведение сил инерции точек твёрдого тела к простейшему виду.
-
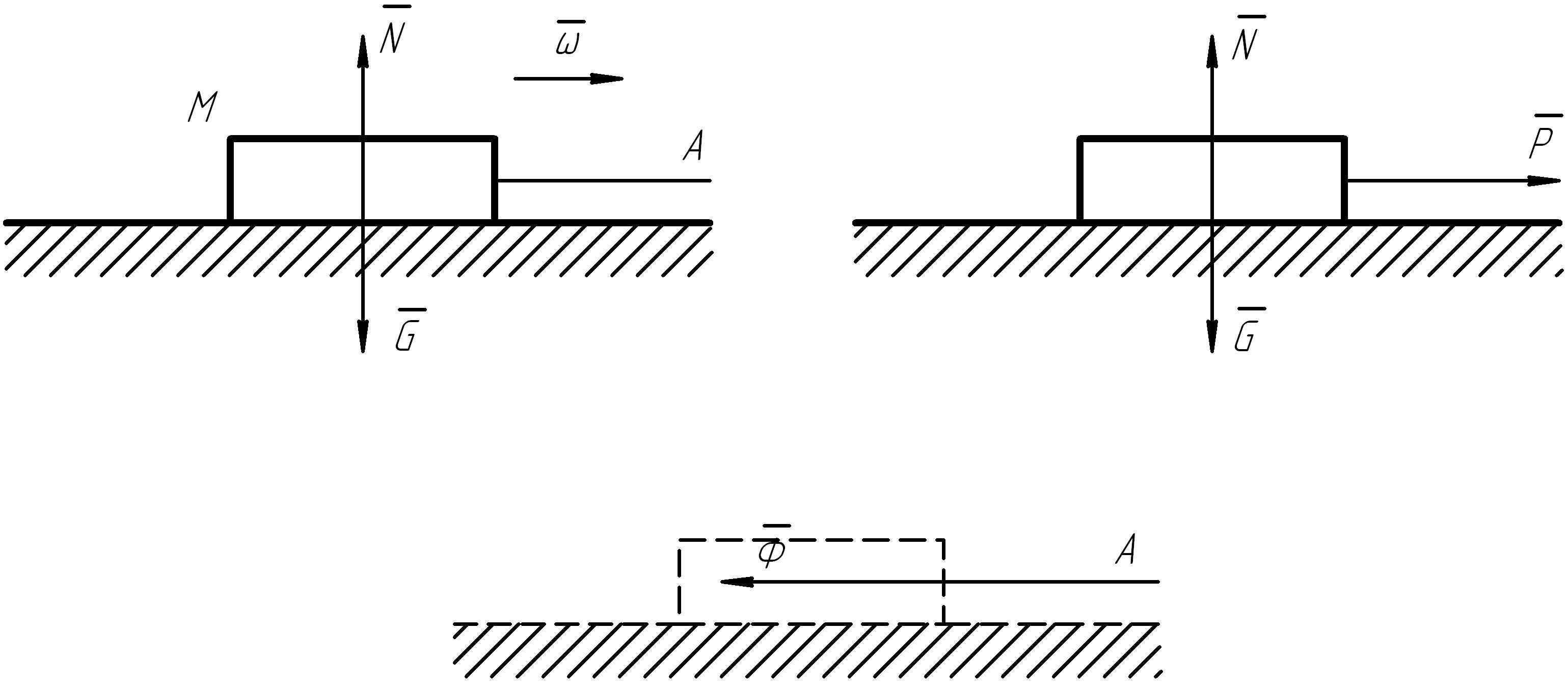
Сила инерции материальной точки
Если в результате
механического воздействия некоторого
тела А на материальную точку М
массой m
эта точка
получает ускорение
![]() ,
то сила
,
то сила
![]() ,
выражающая действие тела А на точку М,
определяется вторым законом динамики
,
выражающая действие тела А на точку М,
определяется вторым законом динамики
![]() (11.1)
(11.1)
По закону равенства
действия и противодействия со стороны
материальной точки М
на тело А
действует
сила
![]() ,
равная по модулю силе
,
равная по модулю силе
![]() и направленная по той же прямой в
противоположную сторону
и направленная по той же прямой в
противоположную сторону
![]() или
или
![]() (11.2)
(11.2)
|
|
|
|
|
Сила
|
-
Принцип Даламбера для материальной точки и
механической системы
|
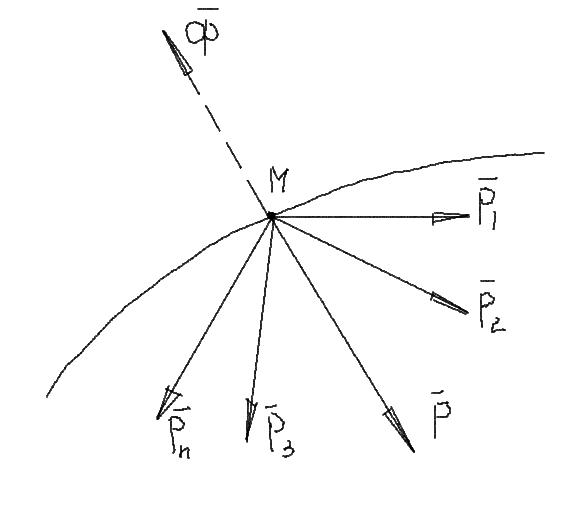
Для материальной точки
Предположим, что
материальная т. М
под действием системы сил
Основное уравнение динамики имеет вид
так как
|
|
Принцип Даламбера для материальной точки Геометрическая сумма всех приложенных к точке сил и силы инерции этой точки равны нулю.
|
|
|
|
Для несвободной механической системы При изучении движения несвободной механической системы применяют принцип освобождаемости от связей. Рассмотрим несвободную механическую систему, состоящую из n материальных точек. Применим к каждой точке Mi принцип Даламбера:
где
|
|
|
|
Принцип Даламбера для i-ой точки несвободной механической системы В любой момент времени геометрическая сумма равнодействующей задаваемых сил, равнодействующей реакции связей и силы инерции для каждой материальной точки несвободной механической системы равна нулю.
Сложим все n уравнений (11.4)
где
|
|
Принцип Даламбера для механической системы В любой момент времени для всякой несвободной механической системы геометрическая сумма главных векторов задаваемых сил, реакций связей и сил инерции материальных точек системы равна нулю.
|
|
Проведём из произвольного неподвижного центра О в каждую точку системы Mi радиусы векторы ri. Умножим векторно ri на сумму векторов левой части равенства (11.4)
Сложим все n уравнений
здесь
|
|
Принцип Даламбера «в моментах» В любой момент времени для всякой несвободной механической системы геометрическая сумма главных моментов задаваемых сил, реакций связей и сил инерции материальных точек системы относительно любого неподвижного центра равна нулю.
|
-
Приведение сил инерции точек твёрдого тела к простейшему виду
|
К системе сил
инерции твёрдого тела можно применить
метод Пуансо – метод приведения сил
к некоторому центру, рассмотренный в
статике. В динамике за центр приведения
сил инерции выбирают обычно центр
масс тела – точку С. Тогда в результате
приведения получится сила
где радиусы-векторыri проведены во все точки тела из центра масс. |
||
|
Дальнейшая
задача состоит в том, чтобы определить
формулы, по которым можно рассчитать
главный вектор
|
||
|
Количество движения системы
Продифференцируем это выражение по времени:
Пользуясь этим выражением, получим главный вектор сил инерции точек твёрдого тела при любом её движении
остаётся
определить
|
||
|
Поступательное движение Ускорения всех точек тела геометрически равны ускорению центра масс. При этом условии:
так как
|
||
|
При поступательном движении силы инерции твёрдого тела приводятся к равнодействующей силе, приложенной в центре масс тела равной по модулю произведению массы тела на модуль его ускорения направленной противоположно этому ускорению.
|
||
|
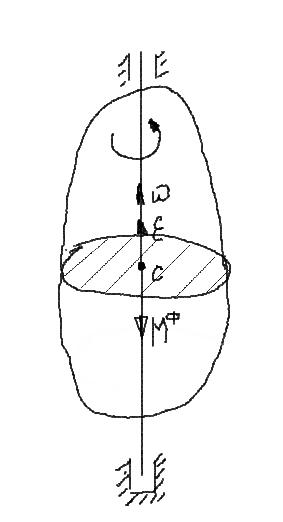
Вращение твёрдого тела, имеющего плоскость материальной симметрии, вокруг неподвижной оси, перпендикулярной к этой плоскости.
В
этом случае неподвижная ось вращения
тела является главной осью инерции
тела в т. О.
Каждой т. Мi
соответствует т. Мi
такой же
массы, симметричная относительно
заданной плоскости. Из кинематики
известно, что ускорения всех точек,
лежащих на одной прямой, параллельных
оси вращения, геометрически равны.
Поэтому силы инерции
|
||
|
|
||
|
Отсюда следует, что в точке Мi приложена равнодействующая сил инерции всех точек тела, лежащих на перпендикуляре к плоскости симметрии, восстановленном в этой точке. Таким образом, сложение сил инерции точек тела в этом случае движения сводится к сложению сил инерции точек материальной плоской фигуры, имеющей массу данного тела и тот же момент инерции относительно оси вращения. |
||
|
Приведём силы
инерции точек фигуры к центру её
вращения О.
При приведении получим силу, приложенную
в этом центре и пару сил, лежащих в
плоскости фигуры. Сила равна главному
вектору, определяемому формулой
(8.11). Он направлен противоположно
ускорению центра масс
Для определения момента пары разложим силу инерции каждой точки на вращательную и центробежную силу инерции, направленные в стороны, противоположные соответствующим ускорениям. Их модули определим по формулам:
Так как линии действия центробежных сил инерции проходят через центр вращения О, то искомый момент пары равен сумме моментов вращательных сил инерции относительно т. О.
здесь
Таким образом
|
||
|
Вращение твёрдого тела, имеющего плоскость материальной симметрии, вокруг центральной оси, перпендикулярно к этой плоскости.
|
||
|
|
|
|
|
Таким образом, если твёрдое тело, вращается вокруг неподвижной оси, которая является его главной центральной осью инерции, то силы инерции точек тела приводятся к паре сил, лежащей в плоскости материальной симметрии тела, момент которой определяется по формуле (11.13).
|
||
|
Плоское движение твёрдого тела, имеющего плоскость материальной симметрии
|
||
|
|
(11.14)
|
|
|
Таким образом, если твёрдое тело, имеющее плоскость материальной симметрии, движется параллельно этой плоскости, то силы инерции точек тела приводятся к силе, приложенной в центре масс и равной главному вектору сил инерции , и к паре сил, лежащей в плоскости материальной симметрии (система уравнений (8.14) .
|
||