ЛЕКЦИИ ТЕОРМЕХ / Лек13Д(през)

ТЕМА: ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ

ЛЕКЦИЯ 13Д

ОБОБЩЁННЫЕ ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ

1. Обобщённые координаты и обобщённые скорости.

2. Обобщённые силы.

3. Выражение обобщённых сил через проекции сил на неподвижные сои декартовых координат. Случай сил, имеющих потенциал.

4. Общее уравнение динамики в обобщённых силах. Условия равновесия сил.

1. Обобщённые координаты и обобщённые скорости

Классификация связей

1-я классификация

Связи
Двусторонние (удерживающие)			Односторонние (неудерживающие)
Конечные	Дифференциальные
	Интегрируемые	Неинтегрируемые
Голономные		Неголономные

2-я классификация

Связи
Стационарные	Нестационарные

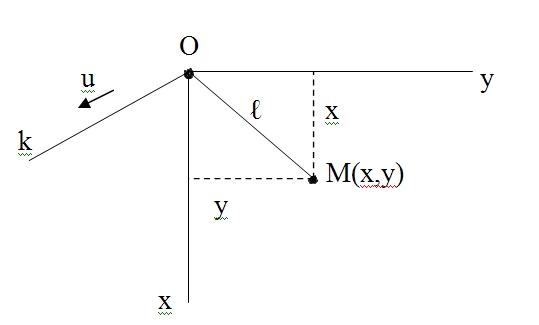
	Пример двусторонней, голономной, стационарной связи – абсолютно жёсткий стержень. Уравнение связи:
	Пример нестационарной связи Уравнение связи:

Независимые величины, заданием которых однозначно определяется положение точек механической системы, называются обобщёнными координатами этой системы.

Пример

Положение рычага АВ с осью вращения Оz вполне определяется заданием его угла поворота . Поэтому угол  можно рассматривать как обобщённую координату рычага. То есть рычаг имеет одну степень свободы

Декартовы координаты любой точки М_i механической системы можно выразить в зависимости от обобщённых координат:

- при стационарных связях

(13.1)

- при нестационарных связях

(13.2)

Для радиуса вектора точки М_i можно записать:

так как , то

(13.3)

Так как обобщённые координаты с течением времени при движении системы изменяются (являются функциями времени):

,

то,

• во-первых, производные от обобщенных координат по времени будут представлять собой обобщенные скорости;

• во-вторых, производная от радиуса-вектора точки М_i будет сложной функцией времени.

2. Обобщённые силы

Рассмотрим механическую систему из n материальных точек М₁, М₂, …, М_n, находящуюся под действием системы сил Предположим, что механическая система имеет S степеней свободы, то есть её положение определяется S обобщёнными координатами

Сообщим обобщённой координате q_j бесконечно малое приращение q_i, не изменяя остальных обобщённых координат механической системы. Тогда точки системы получат бесконечно малые перемещения

Так как эти перемещения допускаются связями, наложенными на систему, то совокупность этих перемещений будет одним из возможных перемещений данной системы.

Силы совершат на перемещениях элементарную работу

(13.4)

Обобщенной силой Q_j, соответствующей обобщённой координате q_j, называют скалярную величину, определяемую отношением элементарной работы действующих сил, на перемещении механической системы, вызванном элементарным приращением координаты к величине этого приращения.

Из определения видно, что размерность обобщённой силы зависит от размерности соответствующей обобщённой координаты

Покажем, что в случае стационарных связей для нахождения обобщённой реакции, соответствующей координате , следует вычислить сумму работ реакций связей на перемещении системы, соответствующем приращению этой координаты, а затем определить обобщённую реакцию связи по формуле

В случае стационарных связей такое перемещение системы является одним из возможных перемещений, и потому сумма работ реакций идеальных связей на этом перемещении равна нулю

Таким образом, при определении обобщённых сил реакции идеальных связей выпадают.

3. Выражение обобщённых сил через проекции сил на неподвижные сои декартовых координат. Случай сил, имеющих потенциал

Рассмотрим механическую систему из n материальных точек, находящуюся под действием сил Предположим, что система имеет S степеней свободы ().

,

Чтобы найти обобщённую силу Q_j, соответствующую обобщённой координате q_j, сообщим координате элементарное приращение , тогда радиус-вектор каждой точки М_i получит приращение, обусловленное приращением только одного аргумента q_j.

(13.5)

Составим сумму работ всех сил, действующих на систему, на возможных перемещениях точек . Для этого воспользуемся выражением элементарной работы силы в виде скалярного произведения

Подставив это выражение в формулу для обобщённой силы, получим

(13.6)

Аналогичное выражение можно получить для обобщённой силы инерции

(13.7)

Рассмотрим случай, когда силы, действующие на механическую систему, имеют потенциал. Тогда проекции этих сил на оси координат равны взятым с обратным знаком частным производным от потенциальной энергии по соответствующим координатам точек:

Подставим эти значения в уравнение для обобщённой силы:

Потенциальная энергия механической системы является функцией декартовых координат точек системы

Учитывая, что декартовы координаты являются функциями обобщённых координат и времени, получим

В случае стационарных связей

Найдём частную производную от потенциальной энергии системы П по обобщённой координате q_j, рассматривая П как сложную функцию обобщённых координат. Эта производная определяется суммой 3n слагаемых. Каждое слагаемое равно произведению частной производной от П по одной из 3n декартовых координат точек на производную от этой декартовой координаты по выбранной обобщённой координате q_j.

то есть

(13.8)

Таким образом, в случае сил, имеющих потенциал, обобщённая сила, соответствующая обобщенной координате q_j равна взятой со знаком «минус» частной производной от потенциальной энергии механической системы по этой координате.

4. Общее уравнение динамики в обобщённых силах.

Условия равновесия сил

Преобразуем общее уравнение динамики (12.7)

Выразим возможное перемещение точки М_i системы через приращения всех обобщённых координат системы:

(13.9)

Общее уравнение динамики примет вид:

Произведём суммирование сначала по точкам системы (i = 1, n), а затем по обобщённым координатам (j = 1,s)

или

Здесь - обобщённая активная сила, соответствующая обобщённой координате q_j

- обобщенная сила инерции, соответствующая обобщённой координате q_j

Тогда общее уравнение динамики будет выглядеть следующим образом:

(13.10)

Тогда

(13.11)

Уравнение (13.11) выражает условия равновесия системы в обобщённых силах.