ЛЕКЦИИ ТЕОРМЕХ / Лек3Д(през)

Лекция 3Д

Момент инерции твердого тела

1. Моменты инерции твердого тела относительно плоскости, оси, полюса.

2. Теорема о моментах инерции относительно параллельных осей.

3. Момент инерции твердого тела относительно любой оси, проходящей через начало координат.

4. Примеры вычисления моментов инерции твердых тел.

1. Момент инерции твердого тела относительно плоскости, оси, полюса

1) Будем рассматривать твердое тело как совокупность материальных точек;

2) Момент инерции твердого тела является мерой его инертности при вращательном движении.

Моменты инерции относительно координатных плоскостей

Моментом инерции твердого тела относительно плоскости называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от точки до плоскости

(3.1)

Моменты инерции относительно осей координат

Моментом инерции твердого тела относительно оси называется скалярная величина, равная сумме произведений массы каждой точки тела на квадрат расстояния от точки до оси

(3.2)

(3.3) - центральный момент инерции

Центробежные моменты инерции

(3.4)

Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции:

.

Момент инерции твердого тела относительно заданной оси можно представить в виде произведения массы тела на квадрат линейной величины, называемой радиусом инерции

(3.5)

2. Теорема о моментах инерции относительно параллельных осей

Так как

После подстановки, получаем

(3.6)

Т.е. из совокупности параллельных осей, ось, проходящая через центр масс тела, характеризуется наименьшим моментом инерции.

3. Момент инерции твердого тела относительно любой оси, проходящей через начало координат

отрезок ОК_i – проекция отрезка ОМ_i на ось υ.

или

4. Примеры вычисления моментов инерции твердых тел

Момент инерции однородного тонкого стержня

Предположим, что стержень длиной ℓ имеет постоянное весьма малое сечение F и плотность ρ.

Масса стержня:

(а)

Разобьём стержень по длине на малые элементы. Масса элемента длиной ∆х_i равна:

Вычислим момент инерции стержня относительно оси Су:

Перейдя к пределу суммы, получаем определённый интеграл

Учитывая (а), получим

Момент инерции однородной круглой пластинки малой толщины

Определим моменты инерции однородной тонкой круглой пластинки относительно осей Сх, Су, Сz (перпендикулярно плоскости круга.)

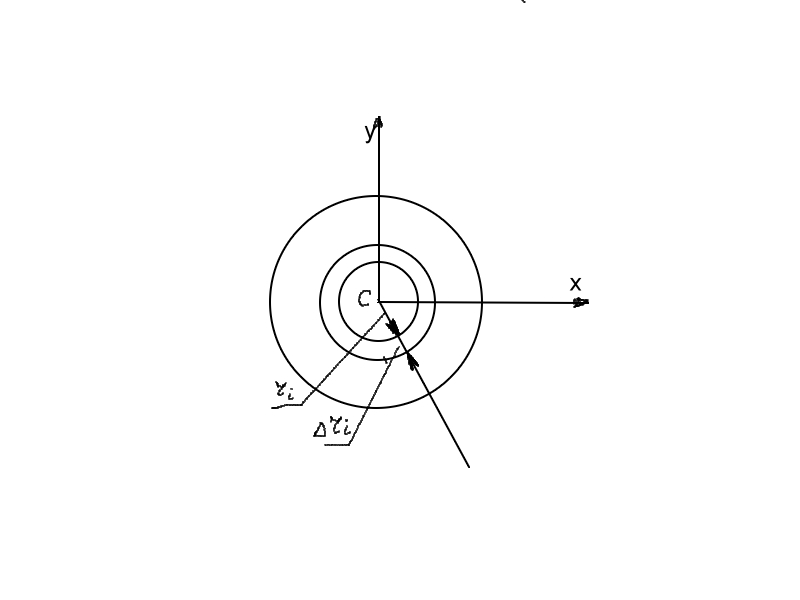
Предположим, что круглая пластинка радиусом R имеет весьма малую толщину h и плотность ρ. Тогда масса пластинки

(в)

Разобьем пластинку на множество элементарных колец радиусом r_i и шириной ∆ r_i. Масса кольца

Так как толщина пластинки мала, то для всех точек пластинки величиной r_i², ввиду малости r_i можно пренебречь. Тогда формулы для моментов инерции пластинки относительно осей координат примут вид:

то есть

так как

то

Вычислим I_cz:

Так как расстояния r_i от всех точек каждого кольца до оси С_z одинаковы, то величину m_i в выражении (в) можно считать не массой точки, а массой всего кольца. Тогда

или

С учётом (в)

Момент инерции однородного круглого цилиндра

Момент инерции цилиндра относительно оси Cz определим как сумму моментов инерции ∆I_cz элементарных пластиной относительно этой же оси

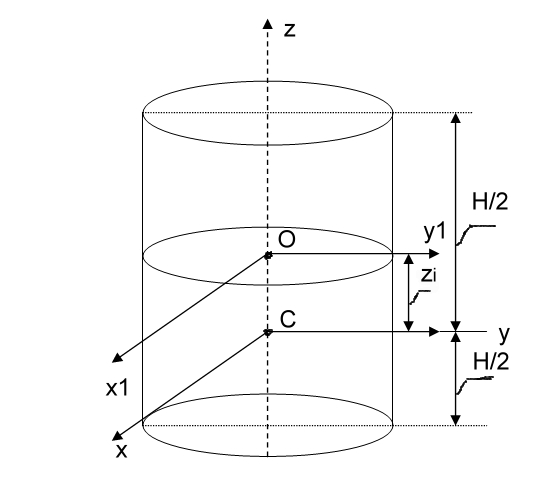
Для вычисления момента инерции цилиндра относительно оси Cy воспользуемся теоремой о моментах инерции тела относительно параллельных осей.

Момент инерции каждой элементарной пластинки относительно оси Оx₁, проведённой по её диаметру, параллельно оси Сx, определиться формулой .

Момент инерции этой пластинки относительно оси Сx, параллельно оси Оx₁ и находится от неё на расстоянии z_i

(c)

Подставив в (c) значение m_i и просуммировав моменты инерции пластинок, получим момент инерции цилиндра

или

(d)

или

(I_cx = I_cy)

Момент инерции полого цилиндра

Момент инерции однородного кругового конуса

Момент инерции однородного шара

Из приведенных формул следует, что моменты инерции конуса, шара и цилиндра, имеющих равные массы и радиусы, относятся как 3:4:5.