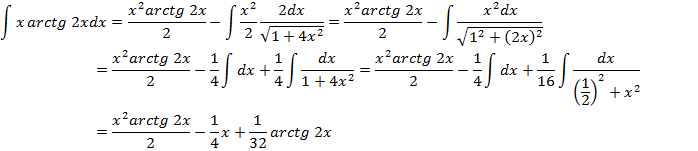Bilety / 29

29. Интегрирование по частям под знаком определенного интеграла. Основные классы функций, интегрируемых по частям. Примеры.

Интегрирование по частям в определённом интеграле

   Интегрирование по частям является методом преобразования интеграла специального вида

.

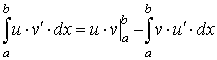   Доказательство. По правилу дифференцирования произведения имеем

.

Интегрируя обе части этого соотношения на интервале [a, b] , имеем

, или .

Учитывая связь дифференциала с производной, окончательно получим .

Эта формула называется формулой интегрирования по частям для определенного интеграла.

Обобщённая формула интегрирования по частям в определённом интеграле

   Многократное применение вышеприведённой формулы интегрирования по частям к интегралу вида

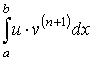
приводит к обобщённой формуле интегрирования по частям

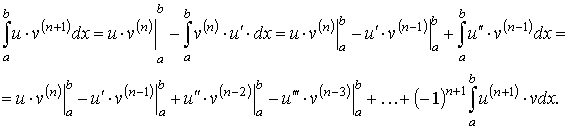
   Для облегчения выполнения интегрирования по частям рекомендуется заполнение таблицы по следующему правилу

+	—	+	…	(-1)n	(-1)n + 1
u	u '	u ''	…	u (n)	u (n + 1)
v (n)	v (n - 1)	v (n - 2)	…	v

   Умножая соответствующие элементы в столбцах этой таблицы с учётом знаков в первой строчке, получим слагаемые вне знака интеграла. Конечное интегральное слагаемое формируется с учётом соответствующего знака в первой строчке, конечного элемента второй строчки и предпоследнего элемента третей строчки таблицы.     При заполнении таблицы составляющие второй строки дифференцируется, а составляющие третьей строчки интегрируется.     Целесообразность применения формулы связаны с тем, что дифференцирование может существенно упростить один из сомножителей (при условии, что интегрирование не слишком усложнит другой).

Пример применения интегрирования по частям в определённом интеграле

   Вычислить интеграл 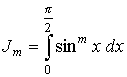.    Решение.

Откуда получаем рекуррентную формулу

.

Применение этой формулы приводит к интегралам

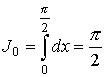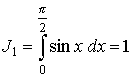, . В частности.

Метод интегрирования по частям:

Классы функций:

Циклическое интегрирование

Пример 1:

dU=dx

Пример 2: