Bilety / 27

27.Определенный интеграл с переменным верхним пределом, его геометрический смысл и производная. Формула Ньютона-Лебница. Двойная подстановка, её линейность. примеры.

Пусть на отрезке [a, b] задана интегрируемая функция . Известно, что определенный интеграл  с геометрической точки зрения численно равен площади криволинейной трапеции.

Будем считать, что нижний предел  закреплен, а верхний предел меняется. Тогда будет меняться и значение интеграла, то есть он будет функцией верхнего предела интегрирования. Зададим любе значение  из отрезка [a, b] и введем в рассмотрение интеграл с переменным верхним пределом:

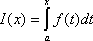  (1)

(От обозначения переменной интегрирования под знаком интеграла величина интеграла не зависит).

 

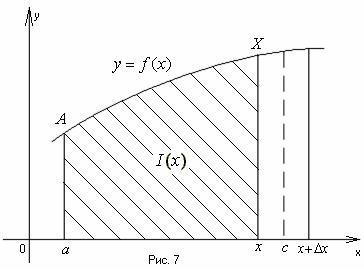
Если , то величина  численно равна площади криволинейной трапеции  (рис. 7).

Очевидно, что эта площадь меняется в зависимости от изменения .

Рассмотрим свойства интеграла

1. Функция непрерывна на [a, b].

Для доказательства фиксируем любую точку  отрезка и зададим приращение . При этом функция  получит приращение

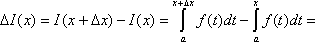(свойство 5)=

 

Устремим , тогда 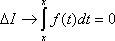 (свойство 2). Это и означает непрерывность функции

2. Функция  дифференцируема на отрезке [a, b].

Доказательство.

Применим теорему о среднем (свойство 9. ) к интегралу  Получаем, что , где  Делим обе части последнего равенства на и переходим к пределу при :

 

так как при переменная  Следовательно, в точке  существует производная , причем

Таким образом, доказано важное свойство:

Производная определенного интеграла от непрерывной функции по его верхнему пределу равна подынтегральной функции, вычисленной при верхнем пределе:

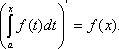  =  (2)

Замечание. Из доказанного свойства следует, в частности, что всякая непрерывная функция имеет первообразную. Согласно п. 5. 2. для непрерывной на [a, b] функции  существует определенный интеграл то есть существует функция 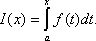 Так как  то  является первообразной для  на отрезке [a, b].

Формула Ньютона-Лейбница. Если f(x) непрерывна на отрезке [a, b], и F(x) - некоторая первообразная функции , то . Док-во. Мы установили, что функция 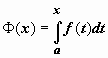- первообразная непрерывной f(x). Так как F(x) - тоже первообразная, то Ф(x) = F(x) + C. Положим в этом равенстве x = a. Так как , то 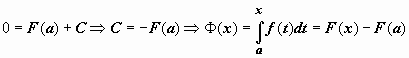В равенстве 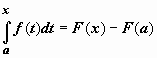переобозначим переменные: для переменной интегрирования t вернёмся к обозначению x , верхний предел x обозначим b. Окончательно, 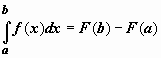. Разность в правой части формулы Ньютона-Лейбница обозначается специальным символом: (здесь читается как "подстановка от a до b"), поэтому формулу Ньютона-Лейбница обычно записывают так: . 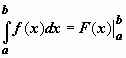Пример применения формулы Ньютона-Лейбница: .
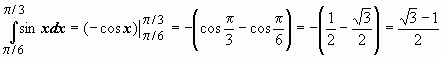