
Bilety / 28
.docx28. Замена
переменной под знаком определенного
интеграла. Тригонометрическая и
гиперболическая подстановки. Примеры.
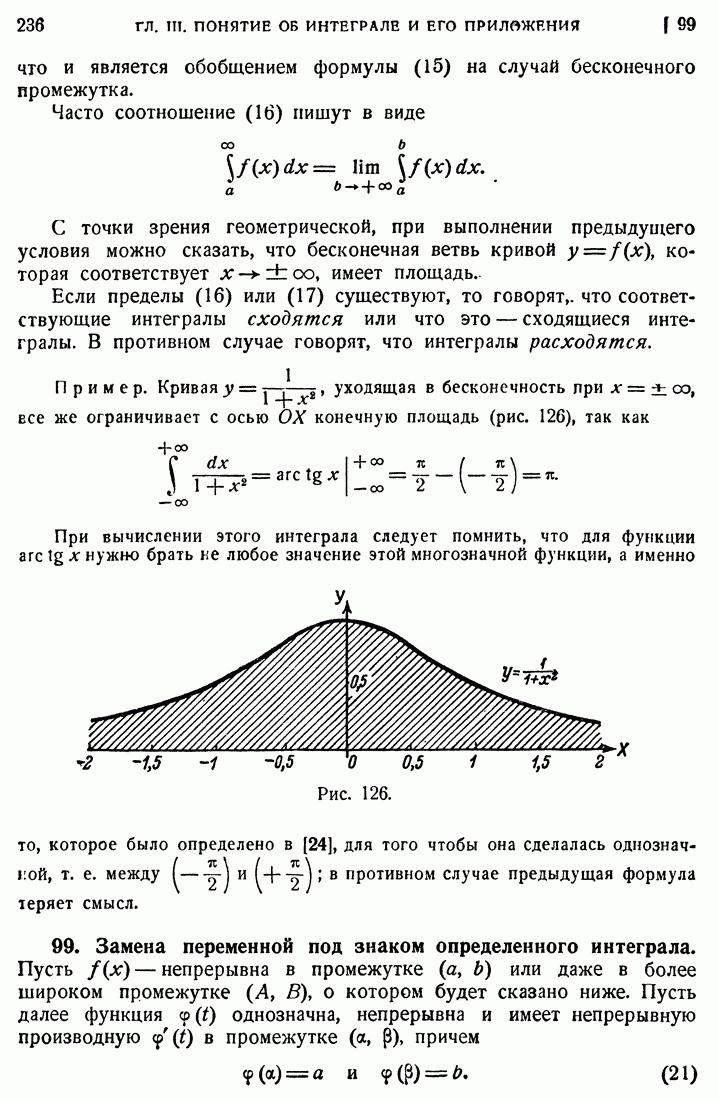


Приведем несколько примеров:
1) 


![]()
![]()
2) ![]()

![]()
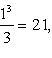
3) 


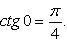
|
Тригонометрические и гиперболические подстановки |
|
|
|
В
данной секции мы рассмотрим вычисление
интегралов вида
Выполнив
замену Каждый из этих трех интегралов вычисляется с помощью специальных тригонометрических или гиперболических подстановок. 1.
Интегралы вида Тригонометрическая подстановка:
2.
Интегралы вида Тригонометрическая подстановка:
Гиперболическая подстановка:
3.
Интегралы вида Тригонометрическая подстановка:
Гиперболическая подстановка:
Примечания:
Мы
полагаем, что . |
|
Пример 1 |
|
|
|
Вычислить
интеграл Решение. Сделаем подстановку Получаем Здесь
для упрощения интеграла мы использовали
формулу |
|
Пример 2 |
|
|
|
Вычислить
интеграл Решение. Применим
гиперболическую подстановку x
= a sh t,
dx = a ch tdt. Поскольку |

 .
.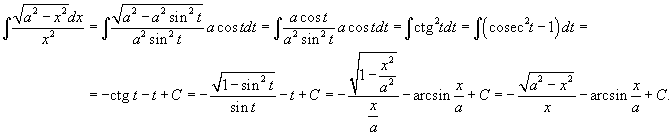
 .
.