МОЙ ДИПЛОМ_1 / 7 Глава 2 РАЗРАБОТКА МОДЕЛИ

Раздел 2

2 Разработка обучаемой модели процесса установки ультрафильтрации

2.1 Модель установки ультрафильтрации в пространстве состояний

В качестве объекта управления была выбрана установка ультрафильтрации (УУФ), точнее один из ее модулей, так как два этих модуля идентичны между собой.

Так как нет физической модели ультрафильтрационного модуля, данная математическая модель стоиться эмпирическим путем, то есть по измеренным параметрам. Данная математическая модель строится по типу «черный ящик».

«Черный ящик» - представление системы, эта максимально простая модель, которая подчеркивает два системных свойства: целостность и обособленность от среды. На рисунке 2.1 показана реальная математическая модель объекта управления в виде «черный ящик» [2, 526].

W(t_k)

ОУ

U(t_k)

x(t_k)

Рисунок 2.1 - реальная математическая модель объекта управления

Для того, что бы более наглядно посмотреть на исследуемый объект управления его нужно представить в виде функциональной схемы сбора информации о текущих значениях входной и выходной переменных. Эта схема представлена на рисунке 2.2.

U(t_k)

W(t_k)

E(t_k)

х(t_k)

y(t_k)

УУФ

ИУ

e(t_k)

+

-

y_М

ИУ

Обучаемая

модель УУФ

U_ИЗМ(t_k)

b

Рисунок 2.2 - функциональная схемы сбора информации о текущих значениях входной и выходной переменных анализируемого объекта управления

ИУ – измерительное устройство;

U(t_k) – значения положения клапана в процентах;

W(t_k) – возмущающее воздействие;

x(t_k) – выходная переменная анализируемого процесса;

Е(t_k) – погрешность измерительного устройства;

y(t_k) – выходная переменная измерительного устройства;

U_ИЗМ(t_k) – измеренное значение положение клапана;

b – вектор параметров модели;

y_М – выходной сигнал обучаемой модели.

После чего составляется уравнения в пространстве состояния для объекта управления (уравнения наблюдения и динамики).

Уравнение наблюдения:

. (2.1)

Уравнение динамики (описывает данный процесс и считаем, что процесс протекает линейно):

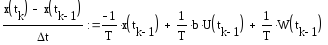. (2.2)

2.2 Анализ устойчивости, наблюдаемости и управляемости

В простейшем случае понятие «устойчивость» системы связано со способностью ее возвращаться (с определенной точностью) в состояние равновесия после исчезновения внешних сил, которые вывели системы из этого состояния [1, 128].

Для того, что бы исследовать систему на устойчивость мы произведем «Z» преобразование уравнения (2.2) и получим:

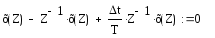. (2.3)

Умножив данное уравнение на Z получим:

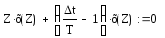. (2.4)

Таким образом, характеристическое уравнение будет иметь вид:

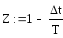. (2.5)

Из этого следует, что так как то

. (2.6)

Таким образом, можно сделать вывод, что при любой постоянной времени Т>Δt система будет устойчива.

Для того, что бы узнать наблюдаема у нас система или нет, для рисунка 2.2 составляем следующую систему уравнений:

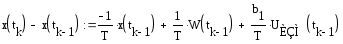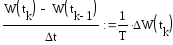, (2.7)

. (2.7)

После чего составляем вектор Z(t) переменных состояния расширенной системы: .

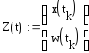Затем составляем вспомогательные матрицы А, G:

,

.

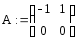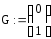После чего составляем вектор которая будет иметь следующий вид:

.

Далее систему уравнений (2.7) можно записать в следующем эквивалентом матричном виде:

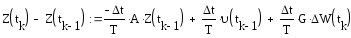. (2.8)

При этом уравнение наблюдения имеет вид:

. (2.9)

Затем уравнение (2.9) принимает вид;

, (2.10)

где: С матрица с коэффициентами .

Число переменных состояния модели объекта (а) n=2. для применения критерия наблюдаемости Калмана составляем матрицу наблюдаемости

.

где:

;

;

;

.

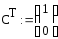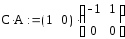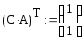Таким образом, матрица наблюдаемости имеет вид:

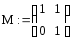. (2.11)

Ранг у этой матрицы будет равен rank(M)=2.

Так как rank(M)=2 равен числу переменных то по критерию наблюдаемости Калмана система наблюдаема.

Из функциональной схемы рисунок 2.2 видно, что при любых b₁≠0 система будет управляема.

2.3 Формулировка задачи обучения

Для того, что бы адаптивная система нормально функционировала ее нужно обучить.

Обучения проводится в два этапа:

а) предварительное обучение;

б) обучение в контуре управления (адаптивное обучение).

Для предварительного обучения с помощью метода наименьших квадратов находим значения, которые и будут в дальнейшим использоваться для предварительно обучения.

Обучение в контуре управления проводиться уже у адаптивной модели УУФ. С помощью рекуррентного метода наименьших квадратов (алгоритм Калмана (РМНК)) происходит обучение уже адаптивной системы управления [3, 165].

2.3.1 Предварительное обучение

Для того, что бы предварительно обучить модель установки ультрафильтрации мы находим коэффициенты с помощью метода наименьших квадратов (МНК), которые нам понадобятся для обучения модели в контуре управления, суть которого заключается в том, что бы сумма квадратов отклонений была минимальна.

Формула МНК:

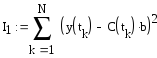, (2.12)

где:

;

.

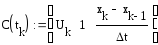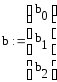Алгоритм обучения.

МНК записанный в матричной форме:

, (2.13)

где:

;

.

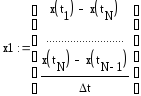По результатам экспериментальных данных входных и выходных значений было выполнено предварительное обучение модели установки ультрафильтрации методом наименьших квадратов (МНК). При этом определялось средние значение возмущающего воздействия параметров модели [4, 125].

2.3.2 Обучение модели УУФ в контуре управления

Обучение модели УУФ в контуре управления проводится уже у адаптивной системы управления.

На рисунке 2.3 показана адаптивная система управления с обучаемой моделью УУФ.

W(t_k)

E(t_k)

ОУ

ИУ

x(t_k)

y(t_k)

U(t_k)

е(t_k)

Регулятор

Обучаемая

модель

УУФ

b(t_k)

X(t_k)

e(t_k)

y_ЗАД(t_k)

Рисунок 2.3 - адаптивная система управления с обучаемой моделью УУФ

Для того, что бы обучить адаптивную систему управления, данную задачу решают минимизацией функционала обобщенной работы :

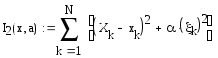, (2.14)

где:

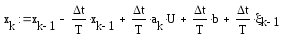. (2.15)

С учетом ограничений и постоянства параметра «а» принимаем:

;

погрешность обучения по выходным значениям;

обучающее воздействие, подаваемое на вход модели.

Смысл обучения адаптивной модели УУФ заключается в том, что выбираются такие «а» и «» которые обеспечивают минимум погрешности обученной модели при минимальных затратах энергии на обучение.

Таким образом, реализация рекуррентного метода наименьших квадратов (Алгоритм Калмана) в матричной форме выглядит следующим образом:

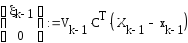; (2.16)

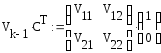; (2.17)

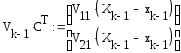; (2.18)

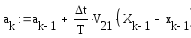; (2.19)

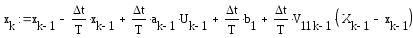. (2.20)

2.4 Вывод

В данной главе были получены следующие результаты:

1) разработаны альтернативные модели УУФ;

2) составлен алгоритм предварительного обучения и выбора наилучшей модели у альтернативных по результатам предварительного обучения;

3) получен критерий эффективности обучения модели УУФ в контуре управления в форме регуляризованного функционала обобщенной работы;

4) составлен алгоритм обучения модели УУФ в контуре управления в форме рекуррентного метода наименьших квадратов (РМНК), обращающий в минимум выбранный критерий эффективности обучения.

53