Лабораторная работа N5

Определение электродвижущей силы термопары методом компенсации

1. Цель работы

Целью данной работы является определение электродвижущей силы термопары и ознакомление с методом компенсации напряжений.

2. Теория вопроса

Электроны в металле свободно перемещаются через весь кристалл, но не покидают его. Как только электрон выходит наружу, весь кусок металла заряжается положительно и втягивает этот электрон обратно. Между тем, обладая кинетической энергией, электроны непрерывно "вылетают" из металла на расстояние, не превышающее атомных размеров, и втягиваются обратно. В результате вблизи поверхности металла образуется электронное облако, а тончайший слой поверхности самого металла становится обладателем некоторого количества избыточных положительных зарядов. Электронное облако с отрицательными зарядами и поверхностью металла с положительными зарядами образуют тонкий двойной электрический слой (рис.5.1). Толщина этого двойного слоя l обычно меньше десяти диаметров атома (dа 10 ^-10 м). Этот двойной электрический слой является своеобразным конденсатором, препятствующим новым электронам выходить изнутри металла наружу. Для того, чтобы удалить электрон из металла в вакуум, необходимо совершить работу А по преодолению этого поля E₀. Эта работа А и называется работой выхода электрона из металла, и ее формула имеет вид: A = e E₀ l = e ₀ (эВ) . (5.1)

Величина ₀ определяется из соотношения (5.1)

и носит название контактного потенциала данного металла. Для различных металлов контактный потенциал меняется в пределах от 1 до 10 В.

Металлы обладают разной плотностью свободных электронов, например, для меди она составляет 8,110 ²² см ^-3, а для калия 0,910 ²² см ^-3. Так как металлы обладают разным потенциалом ₀ и разной концентрацией свободных электронов n, то при соединении двух различных металлов в местах соединений, т.е. в контактных слоях, возникают так называемые контактные электрические явления. Для исследования этих явлений возьмем два куска разных металлов (рис.5.2). Допустим, что в первом из них работа выхода электрона будет А₁, а концентрация свободных электронов n₁, а во втором соответственно А₂ и n₂. Допустим также, что: A₁ < A₂, т.е. (₀₁ < ₀₂ ), а n₁ > n₂.

При соприкосновении металлов электроны получат возможность переходить из одного металла в другой. Диффузия свободных электронов обусловливается причинами: - во-первых, разной работой выхода электронов;

- во-вторых, различной их концентрацией.

Эти два потока диффузии электронов могут быть как параллельными, так и антипараллельными. В нашем случае при ₀₁ < ₀₂ и n₁ > n₂ они будут параллельными.

Поток диффузии электронов прекратится в тот момент, когда в месте контакта возникает двойной электрический слой с электрическим полем E_1,2, уравновешивающим силы диффузии, т.е. возникает контактная разность потенциалов __1,2 = E_1,2 l. Очевидно, что эта контактная разность потенциалов слагается из двух составляющих:

__1,2 = __1,2 + __1,2 , (5.3)

где __1,2 - контактная разность потенциалов, возникающая за счет разной работы выхода электронов; __1,2 - контактная разность потенциалов, возникающая за счет разной концентрации электронов.

Можно строго показать,что: __1,2 = ₀₂ - ₀₁ , (5.4)

где k - постоянная Больцмана, е - заряд электрона, Т - абсолютная температура контакта. Таким образом, полная контактная разность потенциалов будет равна:

Знак (+) в формуле (5.6) ставится в том случае, если два потока диффузии электронов параллельны (₀₁ < ₀₂ и n₁ > n₂) и знак (-) - если потоки антипараллельны (₀₁ < ₀₂ и n₁ < n₂).

Контактная разность потенциалов не создает электрического тока, так как потенциалы электронов, способных менять свое состояние в точности равны. В случае разомкнутой цепи, состоящей из ряда последовательно соединенных различных металлов (рис.5.3), имеющих одну температуру, суммарная контактная разность потенциалов не зависит от прочих металлов, находящихся между ними, а определяется контактной разностью потенциалов между концами цепи (первое правило Вольты).

Суммарная контактная разность потенциалов __BC (см.рис.5.3) равна сумме контактных разностей потенциалов всех контактов, т.е.

__B,C = __1,2 + __2,3 + __3,4

или

k T n₁ k T n₂

__B,C = (₀₂ - ₀₁) + ——  ln —— + (₀₃ - ₀₂) + ——  ln —— +

e n₂ e n₃

k T n₃

+(₀₄ - ₀₃) + ——  ln —— , т. е.

e n₄

k T n₁

__B,C = (₀₄ - ₀₁) + ——  ln —— . (5.7)

e n₄

Из формулы (5.7) видно, что суммарная контактная разность потенциалов разомкнутой цепи определяется лишь контактными свойствами начального и конечного проводников (металлов).

Если составить из нескольких металлов, находящихся при одной температуре, замкнутую цепь, то контактная разность потенциалов в замкнутой цепи равна нулю и не вызывает тока (второе правило Вольты). Для простоты рассмотрим замкнутую цепь, состоящую из двух разных металлов В и С (рис.5.4). При Т₁ = Т₂ =Т суммарная контактная разность потенциалов

__B,C = __1,2 + __2,1, т.е.

Совсем иная ситуация возникает в том случае, если температуры контактов разные, т.е. T₁  T₂. В этом случае формула (5.8) преобразуется в соотношение

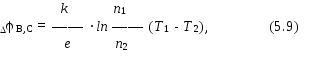
где суммарная контактная разность потенциалов замкнутой цепи, состoящей из разных металлов отлична от нуля. Это контактное явление иногда называют явлением Зеебека, а сама суммарная контактная разность потенциалов __B,C =  называется термоэлектродвижущей силой (термоЭДС):

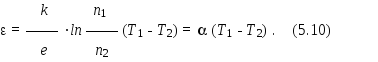ТермоЭДС зависит только от разности температур горячего и холодного спая (Т₁ - Т₂). Коэффициент , называемый удельной термоЭДС, определяется контактными свойствами пары металлов, образующих контакт, и сохраняется величиной постоянной только в определенном интервале температур. Удельная термоЭДС для разных металлических контактных пар меняется:  = (2 - 10) мкВ/град .

Когда электрическая цепь состоит только из двух различных проводников (рис.5.4), она называется термоэлементом или термопарой. Термопары схематически обозначаются, как указано на рис.5.5 .

ТермоЭДС может возникнуть в цепях, состоящих из одного и того же металла, но имеющих различного рода неоднородности (вызванные разными механическими воздействиями), при наличии в цепи температурных перепадов. С другой стороны, термоЭДС термопары не меняется при последовательном включении в цепь любого количества других металлов, если появляющиеся при этом дополнительные места контактов поддерживать при одной и той же температуре. Если через контакт, образованный двумя разными металлaми (см.рис.5.2), пропустить электрический ток, то в зависимости от направления тока I и направления электрического поля Е_1,2 в контакте, это контактное поле либо будет тормозить упорядоченое движение электронов, либо, наоборот, ускорять его. В первом случае кинетическая энергия упорядоченного движения электронов при прохождении через контакт уменьшается, а это эквивалентно охлаждению контакта, а во втором - кинетическая энергия электронов возрастает, т.е. это эквивалентно нагреванию контакта.

Выделяющееся (поглощающееся) в контакте количество тепла Q_П, избыточное по сравнению с джоулевой теплотой Q, пропорцианально протекающему через контакт количеству электричества q, т.е. Q_П =  q =  I t . (5.11)

Это явление, обратное явлению Зеебека, называют явлением Пельтье. Коэффициент , зависящий от природы находящихся в контакте материалов [  = (10^-2 - 10^-3) Дж/А с], называется коэффициентом Пельтье.

В настоящее время явление Пельтье используется для устройства холодильной машины, только контакты здесь выполнены из различных полупроводников.

Томсон предсказал и обнаружил явление, сущность которого заключается в следующем. Если нагревать один из концов однородного металлического проводника, то тепловые скорости электронов в нем возрастают и появляется преобладание диффузионного потока электронов от нагретого конца к холодному. Возрастание энергии электронов в некоторых областях проводника означает, что проводник становится неоднородным. В неоднородных проводниках наблюдается явление Пельтье, поэтому явление Томсона можно рассматривать как явление Пельтье в однородном металле с температурным градиентом.

Опыт показывает, что количество тепла Q_, выделившееся (поглощенное) в однородном металлическом проводнике с разностью температур на его концах Т₁ -Т₂ за время t прохождения тока I равно: Q_ =  (T₁ - T₂) I t , (5.12)

где  - коэффициент Томсона, зависящий от природы металла;  = (10^-4 - 10^-5) [ Дж/А с град ] .

За положительное направление тока I принимают направление, совпадающее с направлением градиента температур _T/ _x, т. е. от холодного конца проводника к горячему (при I > 0 тепло выделяется, т.е. Q_ > 0).