Критерии равновесных и самопроизвольных процессов
В соответствии со вторым началом термодинамики критерием самопроизвольного процесса является рост энтропии. Если энтропийный фактор, определяющий возможность самопроизвольных процессов, соотносится с энтальпийным следующим образом: TdS≥dU (а для изобарного процесса TdS≥dН), - то из уравнений (4.3) и (4.4) следует
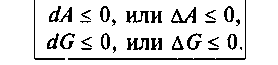(4.5
и 4.6)
Равенство означает равновесный процесс, знак "меньше" характеризует самопроизвольный процесс. Соотношения (4.5) и (4.6) являются основополагающими для расчетов и определения условий равновесных и самопроизвольных процессов для неизолированных систем.
В практических расчетах значения энергии Гиббса применяют чаще, чем энергии Гельмгольца. На практике химические и физико-химические процессы чаще проводят при постоянном давлении, нежели при постоянном объеме, т. е. в изобарных условиях, которые характеризуются энергией Гиббса.
Рассмотрим протекание самопроизвольных процессов и условий равновесия с помощью рисунка.
Как и в случае изменения энтропии, рассмотрим самопроизвольный I, равновесный II и несамопроизвольный III процессы. Сопоставим изменения энтропии и энергии Гиббса. Изменение энергии Гиббса (энергии Гельмгольца) является в принципе зеркальным отображением изменения энтропии. Энергия Гиббса (Гельмгольца соответственно) уменьшается в самопроизвольном процессе, в отличие от энтропии, которая увеличивается.
В условиях равновесия энергия Гиббса и энергия Гельмгольца достигают минимума, в то время как энтропия - максимума.
Еще раз подчеркнем, что энтропия является критерием направленности процесса в изолированных системах, а энергия Гиббса и энергия Гельмгольца - в неизолированных системах.
Для осуществления несамопроизвольных процессов, когда ΔG>0 или ΔА>0, необходимо затратить энергию, находящуюся вне системы в окружающей ее среде.
В обобщенном виде изменения энтропии, энергии Гиббса и Гельмгольца в различных процессах для изолированных и неизолированных систем приведены в таблице.
Итак, для определения направления процесса, а также для определения возможности самопроизвольного процесса необходимо знать изменение энергии Гиббса (энергии Гельмгольца), т. е. выполнение условий (4.5) и (4.6).
Определить изменения энергии Гиббса можно двумя способами. Первый из них основан на использовании уравнения 4.4, а второй - на рассмотрении энергии Гиббса как функции состояния. Рассмотрим два этих способа на примерах. Обратимся сначала к расчету энергии Гиббса и энергии Гельмгольца с помощью уравнений 4.3 и 4.4
Рассмотрим второй способ расчета изменении энергии Гиббса как функции состояния системы. По аналогии с определением энтальпии реакции
изменение
энергии Гиббса в результате
химической реакции равно разности
энергий Гиббса продуктов реакции и
исходных веществ, участвующих в этой
реакции,
т.е
(4.7)
Характеристические функции, термодинамические уравнения состояния
Между пятью термодинамическими функциями состояния: внутренней энергией ΔU, энтальпией ΔH, энтропией ΔS, энергией Гиббса ΔG и энергией Гельмгольца ΔA - существует связь. Связь между термодинамическими функциями и основными параметрами системы р, V и Т представлена на рисунке.
Согласно рисунку каждая из четырех прямых характеризует связь между тремя величинами, две из которых являются термодинамическими функциями состояния. При постоянстве двух других третья величина определяет условия самопроизвольного и равновесного процесса. Эти процессы можно представить следующим образом
Наибольшее практическое значение имеют изобарно-изотермические процессы, связь между параметрами которых характеризуется прямой 3.
Все рассмотренные пять термодинамических функций являются характеристическими. В термодинамике принято называть функцию характеристической, если ее значения и значения ее производных разного порядка достаточны для выражения в явной форме всех термодинамических свойств системы. Характеристическими являются функции ΔU, ΔH, ΔG, а также ΔS и ΔA.
Термодинамическим уравнением состояния называется дифференциальная зависимость характеристической функции от параметров, определяющих ее.
Ранее писали, что если подставим в уравнения
и
значение теплоты из уравнения второго
з-на термодинамики для обратимых и
необратимых процессов ТdS≥δQ,
то получим объединенное уравнение
первого и второго з-нов терм-ки для
обратимых процессов:
ТdS=dU+δA
TdS=dU+pdV
Запишем последнее уравнение в явном виде по отношению к внутренней энергии, получим первое термодинамическое уравнение состояния:
(4.8)
(4.9)
Из него следует, что внутренняя энергия является функцией энтропии и объема
то есть энтальпия есть функция энтропии и давления
Продифференцировав уравнение А = U—ТS, получим
(4.10)
то есть энергия Гельмгольца есть функция объема и температуры
Для вывода четвертого уравнения воспользуемся выражением
G=H-TS, продифференцируем его, получим
Так как dH-TdS=Vdp из уравнения (4.9), получим
(4.11)
энергия Гиббса есть функция давления и температуры.
Зная характеристические функции и их термодинамические уравнения состояния, можно полностью получить в явном виде все термодинамические величины изучаемой системы.