Глава 9 трЕхкомпонентные системы

§ 9.1. Применение правила фаз Гиббса к

Трехкомпонентным системам

Для трехкомпонентной системы, на равновесие в которой из внешних факторов оказывают влияние только давление и температура, правило фаз Гиббса выражается уравнением

(9.1)

Отсюда следует, что в трехкомпонентной системе число фаз, находящихся в равновесии, не может быть больше пяти (С = 0, еслиФ = 5), а максимальное число термодинамических степеней свободы, т.е. независимых параметров состояния системы, равно четырём – давление, температура и концентрацииХ₁иХ₂двух компонентов,выраженные в массовых или молярных долях или процентах (С = 4, еслиФ = 1). При выбранных параметрах состояния системы (Р,Т,Х₁,Х₂) полная диаграмма состояния должна быть четырехмерной. В связи с этим состояние трехкомпонентной системы и равновесие фаз в ней рассматривают при постоянном давлении и строят трехмерную пространственную диаграмму состояния в виде прямой трехгранной призмы, основанием которой служит равносторонний треугольник состава, а по высоте откладывается температура. При P = const

(9.2)

Изучение равновесий в трехкомпонентной системе еще более упрощается при постоянных давлении и температуре. В этом случае можно использовать плоскую диаграмму состояния, являющуюся сечением трехгранной призмы, параллельным основанию (диаграмма состава). При P = constилиT = const

(9.3)

§ 9.2. Графическое изображение состава трехкомпонентных систем

Для графического изображения состава трехкомпонентных систем при постоянных РиТприменяются треугольные и прямоугольные диаграммы. Треугольные диаграммы строят по методу Гиббса или по методу Розебума. В каждом из этих методов используется равносторонний треугольник (рис. 9.1.), вершины которого соответствуют чистым компонентамА,В, иС. Фигуративная точка, лежащая на любой из сторон треугольника, изображает состав соответствующей двухкомпонентной системы, а фигуративная точка, находящаяся внутри этого треугольника, – состав состав трехкомпонентной системы.

Определение состава системы при помощи треугольника концентраций можно провести двумя методами: методом Гиббса и методом Розебома.

Метод Гиббса заключается в том, что из данной точки (например, точки О) проводятся перпендикуляры на каждую из сторон. Сумма длин этих перпендикуляров равна высоте треугольникаh, которую принимают за 100 %. Тогда состав трёхкомпонентной системы можно выразить в объёмных процентах с помощью длин перпендикуляров. При этом длина каждого перпендикуляра, опущенного на данную сторону пропорциональна содержанию компонента, отвечающего вершине, лежащей против данной стороны. Например, в т.О:

(9.4)

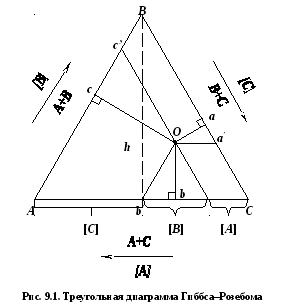
По методу Розебома из данной точки проводятся отрезки, параллельные сторонам треугольника. Сумма этих отрезков равна стороне треугольника, которая принимается за 100 %. Длина каждого отрезка, проведённого к данной стороне, отвечает содержанию компонента, находящегося в вершине, противоположной этой стороне. Например, в точке О:

(9.5)

Наиболее удобным для практического использования является разновидность метода Розебома. В этом случае из точки «О» проводят две прямые, параллельные двум сторонам треугольника до пересечения с третьей. При этом третья сторона разбивается на отрезки соответствующие содержанию всех трёх компонентов (рис. 9.1). Методы Гиббса и Розебома приводят к одинаковому результату, так как стороны и высоты равностороннего треугольника пропорциональны друг другу.

Треугольная диаграмма имеет несколько важных свойств.

1. Точки, лежащие на прямой, проходящей через одну из вершин треугольника и пересекающей противолежащую ей сторону (рис. 9.2), отображают системы с постоянным соотношением концентраций двух компонентов, через вершины которых прямая не проходит. Это следует из пропорциональности длин перпендикуляров, опущенных из любой точки указанной прямой на соответствующие стороны.Так точкиb₁иb₂, лежащие на прямойBb, проходящей через вершинуB, отображают системы с постоянным соотношением концентраций компонентовAиC.

2. Точки, лежащие на прямой, проходящей через две стороны, параллельно третьей (рис. 9.2), отображают системы с постоянным содержанием компонента, которому эта вершина отвечает. Например, в любой точке на линии OO₁, содержание компонентаBодинаково (Ob₃ = O₁b₄).