физ химия / новая папка Савельев / Новая папка / лекция 6

Максимальная полезная работа

как мера химического сродства

Изотерма химической реакции

Константы равновесия определяют условия равновесия, когда концентрации (парциальные давления) являются равновесными. Рассмотрим, например, реакцию Н₂ +I₂ ↔ 2НI. Совсем не очевидно, в каком направлении пойдет эта реакция при Т = 298,15 К, когда парциальные давления исходных веществ и продуктов реакции отличаются от равновесных.

Ответить на этот вопрос поможет уравнение изотермы химической реакции, или, сокращенно, изотерма химической реакции.

Обозначим в общем виде неравновесные парциальные давления реагирующих веществ в соответствии со схемой химической реакции, в виде

Для изобарно-изотермического процесса в соответствии с (5.4) можно записать

6.1

Используя равенство (5.14) и преобразования, аналогичные (5.15)-(5.17), получим

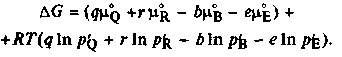6.2

Первое слагаемое правой части уравнения согласно (5.18) равно второе слагаемое равно

т.е.

Изменение энергии Гиббса, определяемое условием (6.1), в отсутствие равновесия равно

6.3

По аналогии с (6.3) и с учетом выражения для константы равновесия К_с получим

6.4

Уравнения (6.3) и (6.4) есть уравнения изотермы химической реакции, первое - для изобарно-изотермического процесса, второе - для изохорно-изотермического

Химическая переменная и химическое сродство

После рассмотрения условий равновесия, которые определяют при помощи констант равновесия и отклонения равновесия, характеризующихся изотермой химической реакции, обратимся к еще одной возможности выразить особенности протекания химической реакции. Речь идет о химической переменной и химическом сродстве.

В любой химической реакции происходит изменение состава системы, который определяется температурой, давлением или концентрацией компонентов. Глубину протекания химической реакции можно выразить с помощью одной переменной, что позволяет строже и проще количественно представить термодинамические параметры. Покажем это на примере реакции получения воды

В общем виде можно записать

Знак "минус" - для исходных веществ, знак "плюс" - для продуктов реакции. Величина ξ есть химическая переменная.

Химическая переменная - отношение изменения числа молей компонента в химической реакции к его стехиометрическому коэффициенту, которое одинаково для всех компонентов и характеризует полноту реакции (иначе - число пробегов или координату реакции). Химическая переменная равна нулю в начале реакции и становится равной единице в том случае, когда все исходные вещества превратятся в продукты реакции.

Таким образом, в пределах одного пробега химическая переменная может принимать значения от 0 до 1

Химическое сродство характеризует отклонение системы от состояния химического равновесия. По аналогии с условием (5.11) химическое сродство (М) можно представить в виде

При М > О неравновесное состояние характеризуется избытком исходных веществ, и для достижения равновесия реакция должна идти слева направо. Когда М < О, реакция идет в противоположном направлении.

Химическое сродство представляется в виде частной производной по химической переменной любого термодинамического потенциала, в частности энергии Гиббса, а именно

В этом выражении член заменяет сумму многих параметров используемую в традиционном (гиббсовском) описании процесса.

Химическое сродство можно выразить в стандартных условиях. Для этого обратимся к уравнениям изотермы химической реакции (6.3) и (6.4). Для газов при давлении, равном атмосферному, когда ⁼ 1 атм первое слагаемое правой части уравнения (6.3) равно нулю (1n1 = 0), т. е

6.5

где М °, ΔG ° - стандартное химическое сродство и изменение энергии Гиббса, когда Т= 298,15 К, а давление равно атмосферному

В соответствии с условием

ΔG = -W'_макс (максимальная работа в изобарно-изотермическом процессе равна обратному по знаку изменению энергии Гиббса)

химическое сродство в стандартных условиях равно максимальной работе изобарно - изотермического процесса:

По аналогии химическое сродство для изохорно-изотермического процесса можно выразить через энергию Гиббса-Гельмгольца

6.6

Соответственно максимальная работа равна

В формулах (6.5) и (6.6) М° есть химическое сродство в стандартных условиях, характеризующее способность веществ вступать в химическую реакцию

Используя формулы эти формулы, можно по величине химического сродства определить константы равновесия, а именно

Уравнения изобары и изохоры химических реакций

Константы равновесия есть величины постоянные при данной температуре. При изменении температуры константа равновесия изменяется и довольно существенно. Одновременно с изменением константы равновесия в соответствии с уравнением (6.5) изменяется химическое сродство ΔG °(М°).

Изменения константы равновесия и направления химической реакции в зависимости от температуры количественно характеризуют уравнения изобары и изохоры химических реакций.

Выведем уравнение изобары химической реакции; обратимся к уравнению (6.3) и перепишем его в виде

6.7

Продифференцируем это уравнение по Т и перепишем его

6.8

Выражение в квадратных скобках, согласно (6.7), есть ΔG/Т, тогда вместо (6.8) получим

6.9

Представим уравнение Гиббса-Гельмгольца в виде

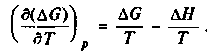6.10

Из уравнения (6.9) вычтем уравнение (6.10) и получим

Уравнение изобары химической реакции в дифференциальной форме, т. е. при постоянном давлении и соблюдении условия δq=dH, выглядит следующим образом

6.11

По аналогии с уравнением изобары уравнение изохоры в дифференциальном виде можно представить как

6.12

Уравнение (6.12) показывает изменение константы равнове сия в зависимости от температу­ры в изохорных процессах, когда выполняется условие (δq=du) - в изохорно-изотермических процессах теплота процесса равна изменению внутренней энергии.

При помощи уравнений изобары и изохоры можно не только определить изменение констант равновесия и самого равновесия в зависимости от температуры, но и найти тепловой эффект химической реакции. Для этого необходимо уравнение изобары (6.11) выразить в интегральной форме; разделив переменные, получим

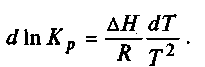6.13

Интегрирование проведем для двух случаев. Первый - когда ΔН = const; тогда после интегрирования имеем

6.14

Во втором случае, когда ΔН≠const, интегрирование уравнения (6.13) дает следующие результаты

6.15

Определение констант равновесия хим. реакций

Можно выделить два метода определения константы хим. реакции:

- 1 й метод ЭКСПЕРИМЕНТАЛЬНЫЙ, который основан на законе действующих масс:

- 2 метод ТЕОРЕТИЧЕСКИЙ, который основан на применении изотермы Вант-Гоффа

ΔG°=ΔH°-TΔS°

1-й метод Расчет равновесия хим. реакции по известной константе равновесия

Этот метод основан на применении ЗДМ, при этом конц-ция одного з реагентов обозначается через х. Зная соотношения, в которых реагируют вещ-ва, можно через эту величину выразить конц-цию остальных реагентов. Затем составляется и решается математическое уравнение, в результате которого находится х и все остальные концентрации.

ксерокопия

2-й метод Метод Темкина -Шварцмана

Для практических целей приходится константу равновесия вычислять при температурах более высоких, чем стандартная. Для этого необходимо знать ΔG_T°, ΔH_T°, ΔS_T° Значительные сокращения математических операций при подсчете указанных величин достигаются методом, предложенным М. И. Темкиным и Л. А. Шварцманом.

Как уже писали, зависимость теплового эффекта химич. реакции от температуры выражается уравнением:

dΔH°/dT=ΔCp°

В интегральной форме это уравнение будет выглядеть:

6.16

Уравнение для расчета изменения энтропии химич. реакции в интегральной форме выглядит как:

6.17

Значения 6.16 и 6.17 подставляем в уравнение ΔG°=ΔH°-TΔS°, получим:

6.18

После подстановки в подынтегральные выражения степенного ряда

получим:

6.19

Проинтегрировав это уравнение, приходим к следующему:

6.20

Раскроем скобки и сгруппируем члены относительно температурных коэффициентов

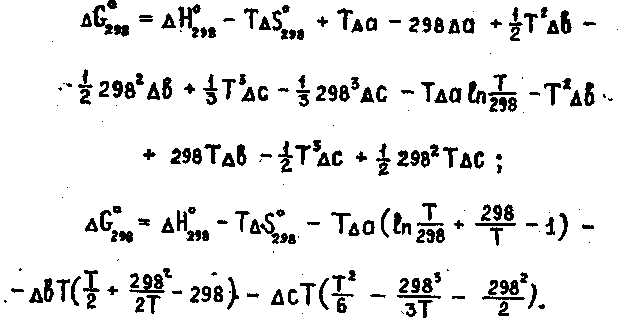6.21

Обозначим:

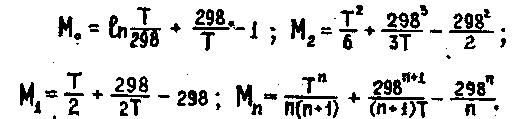
Подставив в уравнение 6.21 значение М₁ , получим:

6.22

Выражение для Мn справедливо, начиная с М₁. Коэффициенты М₀ ... Мn зависят только от температуры. Они рассчитаны и представлены в справочной литературе. Полученное значение ΔG°т, подставив в уравнение lnKp=-ΔG_T°/RT, получим значение константы равновесия для температуры выше стандартной.

9