3.Замкните ключ S1. С помощью движка потенциометра установите по вольтметру напряжение 1,2 В.

4.Зарядите конденсатор, установив переключатель S3 в положение 1 – 2.

5.Разрядите конденсатор через баллистический гальванометр, установив переключатель S3 в положение 5 – 6. Сделайте отсчет по шкале максимального отклонения светового зайчика.

6.Опыт повторите три раза, изменяя напряжение на обкладках конденсатора от 1,2 до 0,8 В. Результаты измерения занесите в табл. 2.1.1.

7.Подключите к клеммам 3 –4 вместо эталонного конденсатора Сэт кон-

денсатор с неизвестной емкостью С1 и выполните измерения, указанные в пп. 3 – 6.

8.Подключите к клеммам 3 – 4 вместо конденсатора С1 конденсатор с не-

известной электрической емкостью С2 и выполните все измерения, указанные в пп. 3 – 6. Результаты измерений по пп. 7 и 8 занесите в табл. 2.1.2.

9. Соедините конденсаторы с электрическими емкостями С1 и С2 сначала параллельно, а затем последовательно, подключите поочередно полученные батареи к клеммам 3 – 4 переключателя S3 и выполните все измерения, указанные в пп. 3 – 6. Результаты измерений занесите в табл. 2.1.3.

2.1.6. Обработка результатов измерений

1.По формуле (2.1.3) вычислите баллистическую постоянную β гальванометра для каждого опыта и вычислите среднее ее значение.

2.По формуле (2.1.4) вычислите электрические емкости конденсаторов С1

и С2 и электрические емкости батарей конденсаторов.

3.Используя найденные экспериментально значения электрических емко-

стей конденсаторов С1 и С2, вычислите по формулам (2.8) и (2.11) электрические емкости батарей конденсаторов.

4. Сравните расчетные значения электрических емкостей батарей конденсаторов с измеренными значениями. Сделайте вывод.

Таблица 2.1.3

Определение электрической емкости батареи конденсаторов при параллельном и последовательном их соединении

2.1.7. Контрольные вопросы

1.Что называют электрической емкостью уединенного проводника? Каков ее физический смысл? Дайте определение единицы измерения электрической емкости в СИ.

2.От чего зависит электрическая емкость уединенного проводника?

3.Выведите соотношение для определения электрической емкости плоского конденсатора.

4.Каков физический смысл баллистической постоянной гальванометра?

5.Как определить электрическую емкость конденсатора с помощью баллистического гальванометра?

6.Как определяется баллистическая постоянная гальванометра в данной работе?

7.Выведите формулы для определения электрической емкости батареи конденсаторов при параллельном их соединении.

8.Выведите формулы для определения электрической емкости батареи конденсаторов при последовательном их соединении.

9.Объясните, как работает плоский конденсатор. Где запасается энергия электрического поля?

10.Объясните, как работает сферический конденсатор. Где запасается энергия электрического поля? Как изменяется емкость батареи сферических конденсаторов при их соединении с помощью одной проволочки?

49

Л а б о р а т о р н а я р а б о т а № 205

2.2. ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ ПРОВОДНИКА

2.2.1.Цель работы

Изучение тока проводимости в металлических проводниках, ознакомление с методами измерения сопротивления проводника и экспериментальное определение удельного сопротивления нихрома.

2.2.2.Содержание работы

Внастоящей работе с использованием закона Ома для однородного участка цепи двумя методами экспериментально определяется сопротивление нихромовой проволоки (67,5% Ni, 15% Сr, 16% Fе, 1,5% Мn) и рассчитывается ее удельное сопротивление.

2.2.3.Описание лабораторной установки

Сопротивление проводника наиболее просто можно измерить при помощи электрических цепей с амперметром и вольтметром. Такие цепи собраны и смонтированы в корпусе лабораторной установки.

На лицевую панель корпуса выведены шкалы вольтметра (0-1,5 В), амперметра (0-260 мА), рукоятка потенциометра (регулятор тока), W3 – переключатель для выбора вида работы, W2 – переключатель для выбора схемы изме-

рений (рис. 2.2.1).

Рис. 2.2.1. Вид экспериментальной установки

К основанию прикреплена колонка со шкалой 2. На колонке смонтированы два неподвижных кронштейна, между которыми натянута исследуемая

50

проволока 3, и один подвижный кронштейн 4, на котором нанесена черта для определения длины измеряемого отрезка проволоки.

Установка позволяет использовать две цепи с разным подключением вольтметра и амперметра, а также позволяет непосредственно измерить сопротивление проволоки с помощью подключения к клеммам 5 (см. рис.2.2.1) внешнего моста постоянного тока.

2.2.4.Методика проведения эксперимента

Влабораторной работе используются первые два метода измерения сопротивления.

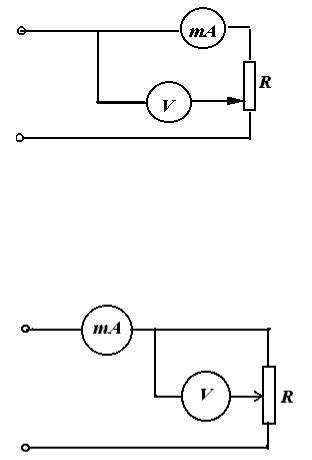
Метод первый (кнопка W2 отжата). Используется электрическая цепь (рис.2.2.2), где миллиамперметр включен последовательно с исследуемой проволокой и с достаточной точностью (зависящей от амперметра) определяет силу тока I в проволоке. Вольтметр дает напряжение U не только на измеряемом участке проволоки, но и на амперметре (сопротивление амперметра

RA = О.15 Ом).

Рис. 2.2.2. Первая схема измерений

Сопротивление R измеряемого отрезка проволоки в этом случае определяется выражением

Метод второй (кнопка W2 нажата).

Рис. 2.2.3. Вторая схема измерений

Используется электрическая цепь (рис. 2.2.3.), где вольтметр включен так, что с достаточной точностью (зависящей от вольтметра) определяет напряжение U на измеряемом отрезке проволоки, миллиамперметр при этом определяет силу тока, который затем ветвится на провод и вольтметр (сопро-

51

тивление вольтметра значительно больше, чем у отрезка провода,

Rv = 2500 Ом).

Сопротивление R на измеряемом участке проволоки в этом случае определяется выражением

2.2.5. Порядок выполнения работы

1. Включите прибор в сеть и установите клавишей W3 вид работы. Отжатая клавиша обеспечивает соединение прибора с мостиком постоянного тока. Этот режим не используется. Нажатая клавиша W3 позволяет измерять сопротивление отрезка проволоки по первому и второму методам, описанным в разделе 4.1.

2.Переключателем W2 сделайте выбор типа схемы измерений по методу первому (см. рис.2.2.2) – клавиша W2 отжата.

3.Установите подвижный кронштейн 4 (см. рис.2.2.1) на деление шкалы, соответствующее примерно 0, 7 длины проволоки от основания.

4.При помощи потенциометра (регулятора тока) установите такое значение силы тока, чтобы вольтметр показывал 2/3 измерительного диапазона.

5.Измерение по первому методу проводите для 10 значений длины прово-

локи от 0,3 l0 до l0, где l0 – полная длина проволоки.

6.Запишите в табл. 2.2.1 показания вольтметра и амперметра.

табл. 2.2.2.

2.2.6.Обработка результатов измерений

Таблица 2.2.1

Результаты измерений и вычислений по первому методу

10

измерений

Таблица 2.2.2

Результаты измерений и вычислений по второму методу

10

измерений

52

ИССЛЕДОВАНИЕ ТЕМПЕРАТУРНОЙ ЗАВИСИМОСТИ СВОЙСТВ СЕГНЕТОЭЛЕКТРИКОВ

2.3.1.Цель работы

Изучение поляризации сегнетоэлектриков; измерение спонтанной поляризованности, коэрцитивного поля и исследование их температурных зависимостей.

2.3.2.Содержание работы

Вработе исследуются зависимости изменения поляризованности образ-

ца РS от напряженности электрического поля Е0 при нагревании сегнетоэлектрика триглицинсульфата в интервале от комнатной температуры до точки Кюри.

2.3.3.Описание лабораторной установки

Специальная электрическая цепь (рис. 2.3.1) позволяет наблюдать петлю гистерезиса на экране осциллографа.

Рис. 2.3.1. Принципиальная электрическая схема экспериментальной установки

От сети через трансформатор напряжение подаётся на делители напряжения: резисторный R1, R2 и ёмкостной С, С0. Напряжение на делителях измеряется вольтметром V. С потенциометра R1 напряжение подаётся на горизонтально отклоняющие пластины осциллографа. Амплитуду этого напряжения Ux можно изменять, вращая ручку потенциометра R1.

Исследуемый образец в виде пластины с электродами представляет собой сегнетоэлектрический конденсатор электрической ёмкостью С, много

меньшей ёмкости вспомогательного конденсатора С0. Напряжение со вспо-

54

могательного конденсатора С0 подаётся на вертикально отклоняющие пластины осциллографа.

Сегнетоэлектрик помещён в нагреватель, температура в котором измеряется термометром.

Внимание ! Не прикасайтесь к токонесущим частям электрической цепи. По достижении точки Кюри, когда петля гистерезиса превратится в слегка наклонную линию, немедленно отключите нагреватель.

2.3.4. Методика проведения эксперимента

На горизонтально отклоняющие пластины осциллографа подаётся на-

пряжение Ux, прямо пропорциональное напряжению U, приложенному к резисторному делителю,

Так как С <<С0, практически всё напряжение U, приложенное к ёмкостному делителю, падает на сегнетоэлектрическом конденсаторе с расстоянием между электродами d, тогда напряжённость поля в нём будет:

Таким образом, горизонтальное отклонение луча осциллографа, определяемое напряжением

получается прямо пропорциональным напряжённости Е в сегнетоэлектрике. На вертикально отклоняющие пластины подаётся напряжение со вспо-

могательного конденсатора, пропорциональное его заряду q0

Так как сегнетоэлектрический и вспомогательный конденсаторы включены последовательно, заряды их одинаковы. Поэтому

где q – заряд на сегнетоэлектрическом конденсаторе.

Так как q равен произведению поверхностной плотности заряда σ на площадь пластины конденсатора S, а σ равна электрическому смещению D, то

а поляризованность PG выражением (2.26) и в соответствии с соотношением

(2.27)

Следовательно, вертикальное отклонение луча прямо пропорционально поляризованности Р сегнетоэлектрика.

Результирующее смещение электронного луча определяется напряжениями Uх и UY одновременно, поэтому в соответствии с формулами (2.3.3) и (2.3.9) он «выписывает» на экране в определённом масштабе графическую зависимость Р(Е) за цикл изменения напряжённости поля.

Рис. 2.3.2. Кривая гистерезиса сегнетоэлектрика

Определяя по графику на экране осциллографа длину отрезка lY (рис. 2.3.2) в делениях измерительной сетки и цену деления СY сетки по вертикальной оси, на основании соотношения (2.3.9) для спонтанной поляризованности получим

Используя (2.3.2), определяя длину отрезка lx (рис.2.3.2) в делениях сетки и цену деления С, находим коэрцитивное поле по формуле

56

При исследовании температурных зависимостей РS и EC измерения

отрезков lx и lY проводятся в интервале температур от комнатной до точки Кюри.

2.3.5. Порядок выполнения работы

1.Подготовьте осциллограф к работе так, как рекомендуется в описании, помещенном на лабораторном столе.

2.Включите электрическую цепь. Изменяя с помощью потенциометра R1 напряжение, подаваемое на вход X осциллографа, а также меняя усиления по X и Y, получите на экране петлю гистерезиса, типа представленной на рис. 3.3.1.

3.При комнатной температуре определите длины отрезков lx и lY в делениях измерительной сетки. По термометру определите температуру в нагревателе. Запишите эти результаты в табл. 2.3.1.

ВНИМАНИЕ !!! При последующих измерениях нельзя изменять положения ручек на панели осциллографа и потенциометра R1, иначе все измерения придётся повторять сначала.

4.Тумблером, находящимся на нагревателе, включите нагреватель. Изме-

ряйте длины отрезков lx и lY через каждые один – два градуса. Когда при температурах, близких к точке Кюри, петля начинает быстро и значительно изменяться, замеры проводите через один градус.

5.Окончив измерения по п. 4, отключите нагреватель.

6.Определите цену деления измерительной сетки по горизонтальной оси

Сx. Для этого осторожно выньте штекер «Y» из гнезда «вход Y» осциллографа. Положение ручек осциллографа и R1 менять всё ещё нельзя! Определите

длину горизонтальной светящейся линии Lx в делениях сетки. По показаниям вольтметра определите соответствующее эффективное значение напряжения

Uэфф.

7. Определите цену деления измерительной сетки по вертикальной оси СY. На вход Y осциллографа подайте контрольный сигнал. Положение ручек осциллографа по-прежнему не изменяйте. Если контрольный сигнал надо ослабить, то пользуйтесь для этого только делителем напряжения (положения 1:10 или 1:100) на панели осциллографа. Определите длину вертикальной светящейся линии LY, соответствующей контрольному сигналу, в делениях сетки. По показателям делителя осциллографа заметьте, во сколько раз ослаблен сигнал (в 1,10,100 раз, соответственно N= 1,10,100).

8.Все результаты по пп. 6 и 7 запишите в табл. 2.2.2.

9.Параметры установки, необходимые для расчетов (указаны на лабораторной установке), запишите в табл. 2.3.3.

57