
- •ПРЕДИСЛОВИЕ
- •Глава 1. МАТЕМАТИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
- •Лабораторная работа № 1
- •Лабораторная работа № 2
- •Лабораторная работа №3
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Высота
- •подъема
- •груза
- •Контрольные вопросы
- •Лабораторная работа № 5
- •Лабораторная работа № 6
- •Таблица 4.15
- •Обработка результатов прямых измерений
- •Результаты вычислений
- •Таблица 5.2
- •Параметры лабораторной установки
- •Таблица 5.3
- •Результаты эксперимента и обработки результатов
- •Стальной брус
- •Латунный брус
- •6.1. Гармонические колебания
- •6.2 Затухающие колебания
- •6.3 Вынужденные колебания
- •Лабораторная работа № 9
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа № 10
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №11
- •Цель работы
- •Описание лабораторной установки
- •Содержание работы
- •Методика эксперимента
- •Порядок выполнения работы
- •Определение периода собственных колебаний маятника
- •Изучение вынужденных колебаний маятника
- •Обработка результатов измерений
- •Контрольные вопросы
- •Цель работы
- •Содержание работы
- •Описание лабораторной установки
- •Методика проведения эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Цель работы
- •Содержание работы
- •Описание моделирующей программы
- •Порядок выполнения работы
- •Анализ результатов моделирования
- •Контрольные вопросы
- •ГЛАВА 7. ВОЛНОВОЕ ДВИЖЕНИЕ
- •Методика эксперимента и описание установки
- •Контрольные вопросы
- •Описание лабораторной установки
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №18
- •Цель работы
- •Содержание работы
- •Методика проведения численного эксперимента на ЭВМ
- •Порядок выполнения работы
- •Завершение работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Лабораторная работа №19
- •Методика эксперимента
- •Порядок выполнения работы
- •Обработка результатов измерений
- •Контрольные вопросы
- •Таблица 9.1
- •Таблица 9.2
- •Таблица 9.3
- •Глава 10. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
- •10.1. Поведение молекул в приповерхностном слое жидкости
- •10.2. Коэффициент поверхностного натяжения
- •10.3. Давление под изогнутой поверхностью жидкости
- •10.4. Краевой угол
- •Добавочное давление под изогнутой поверхностью
- •Поэтому высота жидкости в капилляре равна
- •Лабораторная работа № 22
- •Цель работы
- •Содержание работы
- •Порядок выполнения работы
- •Обработка результатов измерения
- •Контрольные вопросы
- •ОГЛАВЛЕНИЕ
Глава 10. ПОВЕРХНОСТНОЕ НАТЯЖЕНИЕ
10.1. Поведение молекул в приповерхностном слое жидкости
Жидкое состояние (как и твердое) характеризуется тем, что потенциальная энергия межмолекулярного взаимодействия U(r) по абсолютной величине превосходит среднюю кинетическую энергию теплового движения <ε>.
Сила притяжения между молекулами быстро убывает с расстоянием, поэтому, начиная с некоторого расстояния rm, взаимодействием можно пренебречь. Это расстояние rm называется радиусом молекулярного взаимодействия. Величина его равна нескольким эффективным диаметрам молекулы.
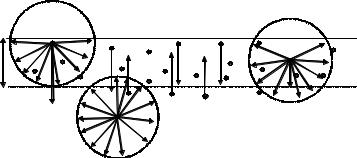
Каждая молекула жидкости испытывает притяжение со стороны других молекул, находящихся в пределах сферы молекулярного взаимодействия данной молекулы. Если молекула находится внутри жидкости, то равнодействующая всех этих сил равна нулю. Если же она находится в тонком приповерхностном слое толщиной rm , то действующие на нее силы не уравновешены, а результирующая сила fпр направлена во внутрь жидкости. Причем, чем ближе молекула к поверхности жидкости, тем больше сила fпр
(рис. 10.1).
fпр |
fпр |
fпр |
rm |
|
|
|
fот |
fот |
Рис. 10.1. Силы, действующие на молекулу в приповерхностном слое
При увеличении поверхности жидкости молекула из глубины жидкости переходит в поверхностный слой, совершая работу против действующих сил fпр. Работа эта совершается при постоянной температуре за счет кинетической энергии молекулы.
Так же как и в механике, устойчивое равновесие системы достигается при минимуме потенциальной энергии. Поэтому поверхность жидкости всегда стремится сохраниться, и вдоль поверхности действуют силы по-
верхностного натяжения.
Поверхностный слой состоит из тех же молекул, что и вся жидкость, и взаимодействие между молекулами в поверхностном слое имеет тот же характер, что и внутри жидкости. Чтобы понять, каков механизм возникновения сил, действующих вдоль поверхности, надо принять во внимание,
176
что, кроме сил притяжения fпр, на молекулы приповерхностного слоя действуют силы, не позволяющие им переместиться во внутрь жидкости. Это силы отталкивания fот, возникающие из–за того, что в направлении, перпендикулярном поверхности жидкости, расстояние между молекулами меньше среднего r<r0 ( рис. 10.1).
Находясь под двойным воздействием со стороны молекул поверхности и молекул, примыкающих к приповерхностному слою, молекулы приповерхностного слоя расходятся в стороны, и расстояние между ними вдоль поверхности становится больше среднего r > r0. Это приводит к возникновению между молекулами сил притяжения, направленных вдоль поверхности и называемых силами поверхностного натяжения Они вместе с силами, действующими перпендикулярно, обеспечивают устойчивость поверхностного слоя.
10.2. Коэффициент поверхностного натяжения
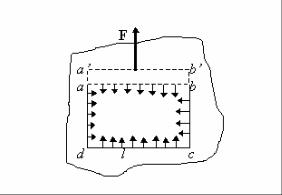
Выделим мысленно часть поверхности жидкости, ограниченную замкнутым контуром abcd (рис. 10.2).
Рис. 10.2. К расчету коэффициента поверхностного натяжения
Стремление этого участка к сокращению приводит к тому, что он действует на граничащие с ним участки с силами, распределенными по всему контуру. На отрезке ab длиной l эта сила будет равна
F =σ l, |
(10.1) |
где σ – величина, называемая коэффициентом поверхностного натяжения.
Пусть внешняя сила F переместит участок контура ab на расстояние dx в новое положение a′b′, увеличив поверхность жидкости. При этом над системой будет совершена работа
dA'= Fdx = σ l dx = σ dS. |
(10.2) |
Из (10.1) и (10.2) получаются две трактовки коэффициента поверхност– ного натяжения
σ = |
F |
= dA' |
, |
(10.3) |
|
l |
dS |
|
|
|
177 |
|
|
|
силовая – как сила, действующая на единицу длины контура поверхности, и энергетическая – как работа, необходимая для квазистатического увеличения поверхности жидкости на единицу при неизменной температуре. Соответственно и единицы измерения для коэффициента поверхностного натяжения могут быть [σ ] = Дж/м2 = Н/м.
10.3. Давление под изогнутой поверхностью жидкости
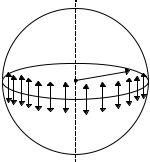
Если поверхность жидкости не плоская, то стремление ее к сокращению приводит к возникновению дополнительного давления ∆P, которое испытывает жидкость (рис. 10.3). В случае выпуклой поверхности дополнительное давление положительно (рис. 10.3, б), в случае вогнутой поверхности – отрицательно (рис. 10.3, в). В последнем случае поверхностный слой, стремясь сократиться, растягивает жидкость.
 .
.
Рис. 10.3. Формы поверхности жидкости
Для определения величины добавочного давления ∆P, рассмотрим сферическую каплю радиуса R , мысленно рассеченную на два полушария (рис. 10.4). Оба полушария притягиваются с силой
F = l σ = 2π Rσ. |
(10.4) |
R
Рис. 10.4. К определению добавочного давления
Эта сила действует на поверхность сечения S=πR2 и |
обеспечивает |
|||||
дополнительное давление ∆Р внутри сферы |
|
|||||
∆P = F |
= |
2πRσ |
= |
2σ |
. |
(10.5) |
πR2 |
|
|||||
S |
|
|
R |
|
||
|
178 |
|
|
|
|
|
Для определения добавочного давления в случае произвольной поверхности используется формула Лапласа
|
1 |
|
1 |
|
|
|
|
+ |
|
(10.6) |
|||
|
R |
|||||
∆P =σ R |
. |
|||||
|
1 |
|
2 |
|
|
|
Радиусы кривизны поверхности R1 и R2 определяются в двух взаимно перпендикулярных направлениях. Для сферы R1=R2=R.
10.4. Краевой угол
Если поверхность разделяет две различные среды, то следует иметь в виду, что поверхностная энергия жидкости (или твердого тела) зависит от свойств обоих веществ.
|
∆lσж-г |
газ |
|
∆lσт-г |
жидкость |
||
θ |
|||
|
∆lσт-ж |
твердое тело |
|
длина контакта ∆l |
|||
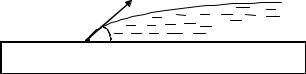
Рис. 10.5. Краевой угол
Рассмотрим условие, при котором три граничащих друг с другом вещества (твердое, жидкое и газообразное) находятся в равновесии (рис. 10.5). Условием равновесия будет равенство нулю сил, приложенных к любой точке линии раздела трех сред
∆lσт–г = ∆lσт–ж + ∆lσж–г cosθ , |
(10.7) |
где σт–г, σт–ж, σж–г – коэффициенты поверхностного натяжения на границах: твердое тело – газ, твердое тело – жидкость и жидкость – газ; θ – угол, отсчитываемый внутри жидкости между касательными к поверхности твердого тела и к поверхности жидкости, называется краевым углом. Из (10.7) находим краевой угол cosυ = (σт–г – σт–ж )/σж–г при условии, что
σт–г – σт–ж /σж–г ≤ 1 .
Если это условие не выполняется, возможны два случая:
1)σт–г>σт–ж+σж–г . В этом случае жидкость неограниченно растекается по поверхности твердого тела θ = 0 (Рис. 10.6, а), что соответствует пол-
ному смачиванию (керосин);
2)σт–ж>σт–г+σж–г . В этом случае поверхность, по которой жидкость граничит с твердым телом, стягивается в точку, θ = π (Рис. 10.6, б), что со-
ответствует полному несмачиванию (ртуть).
179
