KM2016 / FEM2_1 / TEX / МКЭ

2.2Построение системы линейных алгебраических уравнений

2.2.1Матричная форма

Метод конечных элементов сводит решение линейной задачи к решению системы линейных алгебраических уравнений

Здесь ui (i = 1; 2; : : : ; n) - неизвестные, Fi (i = 1; 2; : : : ; n) - заданные свободные члены, fij (i; j = 1; 2; : : : ; n) – коэффициенты при неизвестных. Коэффициенты fij образуют квадратную матрицу, состоящую из n строк и n столбцов

Если обозначить столбец неизвестных u, а столбец свободных членов P , то система линейных алгебраических уравнений (17) принимает матричную форму (16) с матрицей жесткости (18)

Система алгебраических уравнений должна быть невырожденной, то есть иметь единственное решение. Для решения (19) можно воспользоваться, например, методом исключения Гаусса. Однако при применении приближенных методов обычно приходится иметь дело с системами большого порядка n 1, и матрица, вообще говоря, может иметь такую структуру, которая затрудняет получение решения. При этом на точности результата в той или иной степени сказываются неизбежные в процессе вычислений ошибки округления. Одним из важных достоинств метода конечных элементов является то, что он обычно приводит к таким системам алгебраических уравнений, матрицы K которых позволяют эффективно строить решение.

Какой желательно иметь матрицу жёсткости Выясним, какой желательно иметь матрицу K в (19). Пределом мечты была бы система (19) с диагональной матрицей K, когда все

fij = 0 при i 6= j:

В этом случае (19) распадается на отдельные уравнения

fiiui = Fi:

11

Такое может быть, только если в физической системе, рассчитываемой методом конечных элементов, узлы между собой не связаны, то есть по существу системы не существует. Однако теперь уже ясно, к чему надо стремиться: следует так выполнять процесс построения алгебраической системы уравнений, чтобы матрица по возможности содержала больше нулевых коэффициентов и была близка к диагональной, другими словами, желательно, чтобы в каждое уравнение входило относительно небольшое число неизвестных в соседних узлах.

2.2.2Ленточные матрицы

Матрицы, близкие к диагональным, обычно имеют ленточную структуру, когда все ненулевые и некоторые нулевые коэффициенты находятся между двумя линиями, параллельными главной диагонали. Например,

01

0 0 0

B 0 0 C

BC

K = B 0 0 C

BC

где знак заменяет коэффициенты, отличные от нуля. Ленточную матрицу характеризует ширина ленты t = t1 + t2 + 1, равная наибольшему числу коэффициентов в строке в пределах ленты. В данном случае t1 = t2 = 2 и t = 5. Для диагональной матрицы t = 1. При решении системы уравнений с ленточной матрицей участвуют только те коэффициенты, которые расположены в пределах ленты. Число арифметических операций, необходимых для решения системы алгебраических уравнений с полностью заполненной матрицей методом Гаусса, при больших n имеет порядок n3. В то же время для ленточной матрицы при t1 = t2 и t1 n он составляет nt21.

2.2.3Пример ленточной матрицы

Для примера ленточной матрицы обратимся к задачам предыдущего раздела, но с пятью узлами и шестью элементами на рисунке 1, г Аналогично (2.1.2) матрица K будет иметь коэффициенты flt. По смыслу flt они отличны от нуля только для тех узлов l, где перемещение узла t вызывает отличную от нуля силу при условии, что остальные узлы, кроме t, неподвижны. Отсюда при нумерации узлов, показанной на рисунке 1, г, слева от оси x имеем:

01

0 0 0

B 0 0C

BC

12

Здесь t = 3 и матрица K является трехдиагональной.

При применении метода конечных элементов ширина полосы ленточной матрицы зависит от нумерации узлов. Например, если пронумеровать узлы так, как показано на рисунке 1,г справа от оси x, то K примет вид (20). Вообще если элементы имеют несколько узлов, то при t1 = t2 величина t1 равна максимальной по элементам величине наибольшей разности между номерами узлов в отдельном элементе. В первом случае нумерации узлов слева на рисунке 1,г t1 = 1, а при нумерации справа t1 = 2.

2.2.4Предостережение - плохая обусловленность

В некоторых случаях исходная постановка задачи может оказаться настолько плохой, что даже метод конечных элементов не может помочь. И надо ее менять. При этом имеет место система алгебраических уравнений, в которой малые изменения коэффициентов или свободных членов приводят к значительному изменению решения. Такие системы уравнений носят название плохо обусловленных. Выясним, в чем причина плохой обусловленности на примере системы (16), которую перепишем в виде

Рис. 2: Графическое решение системы уравнений (21)

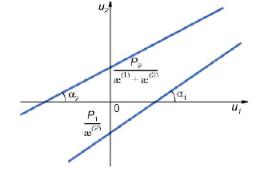
В прямоугольной системе координат u1; u2 на рисунке 2 уравнение прямой будет u2 = u1 tan 1 + g, где – угол между прямой и положительным направлением оси u1, g – отрезок отсекаемый прямой на оси u2. Уравнения (21) описывают две прямые на рисунке 2, а решение (21) представляет собой координаты точки пересечения этих прямых. Здесь

13

Если 1 = 2 и прямые параллельны, то решение системы (21) не существует и она является вырожденной. Если 1 и 2 различаются мало, то система близка к вырожденной. При этом незначительные изменения углов1, 2 сильно скажутся на координатах точки пересечения прямых, то есть на решении. Таким образом, плохая, обусловленность объясняется тем, что система является почти вырожденной.

В качестве примера обратимся к (21). Пусть 1 = 3 = и 2 , то eсть элемент 2 значительно более жесткий, чем элементы 1 и 3. При этом tan 1 tan 2 и система (21) почти вырожденная. В данном случае разумно изменить постановку задачи и считать элемент 2 абсолютно жестким по сравнению с элементами 1 и 3. Это позволяет объединить узлы 1 и 2 в один узел, который обозначим 12, и приложить к нему суммарную силу F12 = F1 + F2. Если в (21) положить u1 = u2 = u12, вычесть из первого уравнения второе и после преобразований пренебречь по сравнению с(2), то задача сведется к одному уравнению

2u12 = F12;

которое и даст решние задачи в этом приближении.

2.3Пример вычислительной программы

В Приложении приведен текст вычислительной программы fem2.cpp, написанной на языке С++ , в котором решается задача о стержне с закреплёнными концами составленном из однородных элементов и нагруженном в местах соединения стержней внешними силами, направленными вдоль оси стержня. В файле входных данных можно задавать число элементов, их размеры и коэффициенты жёсткости. На выходе получаются величины смещений узловых точек - мест соединения стержней. Система линейных алгебраических уравений решается методом обратной подстановки.

Текст программы снабжен подробными комментариями со ссылками на формулы данного раздела.

3Однородный стержень с непрерывной нагрузкой

3.1Континуальная задача

Обратимся к задаче (3) для одного элемента. В общем случае задания q(i)(x) она является континуальной задачей. Для простоты положим c(i) = 1, l(i) = 1, u(ii) = u(ji) = 0 и опустим индекс r , тогда дифференциальное

14

Для общности рассмотрим эту задачу при нулевых граничных условиях

и при граничных условиях общего вида, которые в дальнейшем для краткости будем называть ненулевыми граничными условиями:

Эти условия требуют положительного решения на границах u > 0 и градиентов направленных внутрь. Коэффициент a для простоты будем считать постоянным.

В матричной форме уравнение (22) c граничными условиями (24) будет иметь вид

Необходимо записать для данной задачи матрицу жёсткости K и столбец Q при заданной нагрузке q(x).

3.2Решение задачи первым способом

3.2.1Аппроксимация решения пробными функциями

Согласно схеме метода конечных элементов, разобьем интервал [0; 1] на элементы, соединенные в узлах xi; i = 1; 2; : : : ; n (рисунок 3).

Будем разыскивать приближенное решение задачи (22), (24) среди функций семейства с конечным числом параметров в виде:

Здесь u(x) приближенно представлена функцией y(x) - линейной комбинацией некоторых функций 'i(x) с коэффициентами (параметрами) ui = u(xi) - неизвестными значениями искомой функции в узлах xi. Для того чтобы в (26) y(xi) = yi во всех узлах xi, функции 'i(x) должны удовлетворять условиям

В остальном функции 'i(x), которые носят название пробных, можно выбирать в довольно широких пределах.

15

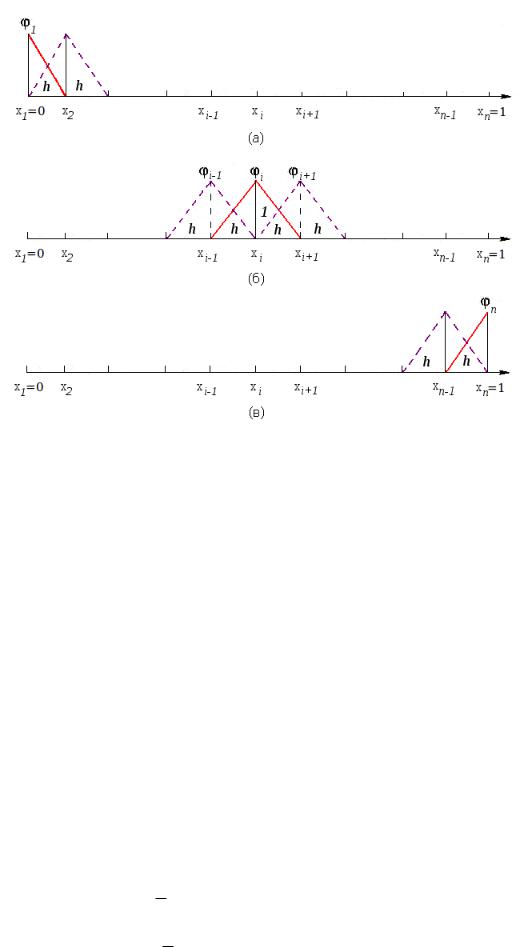
Рис. 3: Пробные функции

Общие требования к пробным функциям состоят в возможности выполнить процесс построения приближенного решения, т.е. на основе (26) при n ! 1 осуществить сколь угодно точно аппроксимацию любой функции, среди которых разыскивается решение задачи.

Очевидно, выбор '(x) играет важнейшую роль как в отношении трудоёмкости расчета, так и точности результата. Метод конечных элементов оперирует в качестве '(x) кусочно-полиномиальными функциями, отличными от нуля в пределах небольшого числа элементов вблизи узла xi. Именно это делает метод максимально эффективным.

Поскольку u(x) по своему физическому смыслу должна быть непрерывной функцией, выберем '(x) в виде кусочно-линейных функций-“домиков” составленных из двух половинок (рисунок 3).

где

'i (x) = h1(x xi + h) (x xi) (xi+1 x); '+i (x) = h1(x xi h) (x xi) (xi+1 x):

16

Здесь (x) - ступечатая функция

1; x 0;

(x) = 0; x < 0:

Каждая такая функция 'i(x); i = 1; 2; : : : ; n, равна единице в xi и нулю во всех остальных узлах. При этом набор функций 'i(x) в (26) будет состоять из непрерывных функций линейных в пределах элементов с изломами в узлах и определяемых своими узловыми значениями ui; i = 1; 2; : : : ; n.

3.2.2Пример аппроксимации пробными функциями

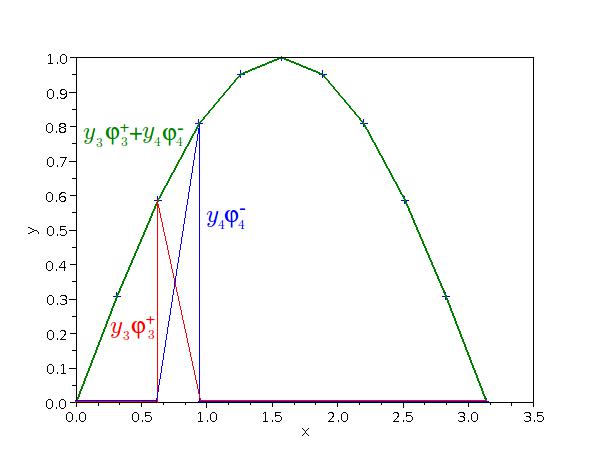
Аппроксимация некоторой функции u(x) (26) пробными функциями (28) представляет собой ломаную линию, состоящую из отрезков прямых, соединяющих точки (xi; yi). Проиллюстрируем это на примере функции u = sin(x); x 2 [0; ] при yi = sin(xi). Ниже приведён текст программы на SCILAB, и на рисунке 4 график, построенный этой программой

Рис. 4: Аппроксимация функции u = sin(x) пробными функциями

Текст программы:

function v = phi_m(x_i,i,x) //'i (x) h = x_i(i) - x_i(i-1);

17

v = 1/h*(x-x_i(i)+h); endfunction

function v = phi_p(x_i,i,x) //'+i (x) h = x_i(i+1) - x_i(i);

v = 1/h*(x_i(i)-x+h); endfunction

x_i = linspace(0,%pi,11); y_i = sin(x_i);

x = 0;

for i = 1:10

xi = linspace(x_i(i),x_i(i+1),10); for j=1:10

x((i-1)*10+j) = xi(j);

y((i-1)*10+j) =y_i(i)* phi_p(x_i,i,xi(j)) + ...

y_i(i+1)*phi_m(x_i,i+1,xi(j)); end

end

scf(1), plot(x_i,y_i,’+’, x,y), xlabel(’x’), ylabel(’y’)

3.2.3Переход к слабой форме

Остаётся определить yi в аппроксимции решения (26). Это можно сделать по-разному путем приближенного удовлетворения уравнению в (22). Однако, поскольку уравнение в (22) содержит вторую производную по x , а уже первая производная по x в (26) терпит разрывы непрерывности в узлах, воспользуемся следующим приёмом. Обозначим

d2u(x)

R(x) = d2x + q(x)

невязку уравнения в (22). Точное решение даёт R(x) = 0, и, следовательно,

для любых функций '(x), которые носят название пробных.

Переход от дифференциального уравнения к интегралльной формулировке той же задачи в вычислительной математике называется переходом от коэффициентной к слабой форме. Такой переход существенно расширяет класс решаемых задач, поскольку интеграл, в отличие от производной, может быть взят и от кусочно-непрерывных функций и дельта-функций.

18

Подставим аппроксимацию искомого решения (26) в интегральное уравнение (29) и затем выполним в (29) интегрирование по частям с учётом граничного условия (24). Тогда вместо (29) получим:

Поскольку разыскивается приближенное решение среди функций семейства с конечным числом параметров в форме (26) и для него, как правило, R(x) 6= 0, то выполнение тестового условия (30) на базе (26) для любых пробных функций невозможно.

3.2.4Метод Галёркина

Смягчим условие (30), потребовав, чтобы оно выполнялось только для n функций 'i(x), которые совпадают с пробными функциями, заданными выражением (28):

Такой приём носит название а метода Галёркина.

В интегральное уравнение (30) теперь входит первая производная функции u. Первая производная дискретной аппроксимации функции u (26) имеет вид

Подставим эту аппроксимацию производной искомого решения в равенство (30) и потребуем его выполнения для каждой из n пробных функций (28). Тогда вместо (30) получим n уравнений

(33) При вычислении первого члена в левой части уравнения (30) следует

учитывать условия на границах.

Нулевые граничные условия В случае нулевых граничных условий вместо (24) имеем

Граничные точки следует исключить из системы уравнений, так как решения на границах известны. Нулевые граничные условия будут выполняться

19

автоматически, если построить аппроксимирующую функцию так, как показано на рисунке 3, т.е. искать решение (26) только для внутренних узлов. Тогда автоматически

'1(0) = 0; 'n(1) = 0;

а также

'i(0) = 0; 8i

Таким образом, в случае нулевых граичных условий

1 du

'i = 0 (35) dx 0

для всех i в (33).

После подстановки граничных условий (35) в (33) получим

0j=1

Это даёт систему линейных алгебраических уравнений относительно yj вида (18) с коэффициентами fij матрицы жёсткости

1

Z

fij = d'i(x) d'j(x)dx; (37) dx dx

0

и правую часть матричного уравнения Qi

Здесь fij = fji и матрица K симметричная, что характерно для метода Галёркина.

Ненулевые граничные условия В случае ненулевых граничных условий граничные точки следует включить в сетку узлов, так как решения на границах неизвестны и должны быть найдены.

Как можно видеть на рисунке 3, пробные функции, построенные для

Для внутренних узлов "домики" полные, и пробные функции определяются по-прежнему выражением (28).

20