1.4. Весовая обработка пачки импульсов

Целесообразно вначале рассмотреть отношение правдоподобия для одиночного сигнала и установить зависимость параметров этого отношения правдоподобия от угловой координаты цели, а затем перейти к пачке импульсов.

Отношение правдоподобия для i-го импульса пачки, при условии, что цель нефлюктуирующая и начальная фаза случайна (усреднённое по случайной начальной фазе), имеет вид

. (20)

Для импульса, отражённого от флюктуирующей цели (релеевские флуктуации)

(21)

(усреднённое по случайной начальной фазе и амплитуде).

Э_i и Z_i - энергия и модуль корреляционного интеграла i –го импульса

- комплексный закон модуляции сигнала.

В (20) и (21) выборочные данные сведены путём предельного перехода к входной реализацииy(t). Отношения правдо- подобия (20) и (21) являются монотонными функциями модуля корреля- ционного интеграла, формируемого оптимальным приёмником обнаруже- ния (функция I₀ - монотонна). Поэтому для решения задачи измерения угловой координаты достаточно использовать отсчёты с выхода приёмника.

Установим зависимость параметров Э_i и Z_i от угловой координаты. Поскольку Э_i и Z_i не зависят от фазы высокочастотного сигнала, то единствен­ным параметром, меняющимся при развёртывании луча (сканировании), являет­ся усиление антенны в направлении на цель. Если бы антенна была остановлена в каком-либо положении, то коэффициент усиления ан­тенны был бы пропорционален произведению коэффициентов усиления на передачу и на приём.

Пусть  - угол цели, _0i - угол оси антенны при приёме i-го импульса пачки. Углы отсчитываются относительно одного направления. Тогда угловое рассогласование цели относительно оси при приёме i-го импульса пачки равно _i=-_0i Нормированный коэффициент усиления антенны при приёме i-го импульса пачки определяется диаграммой направленности по полю f(_i). Поскольку на приём и передачу используется одна антенна, то ампли­туда принимаемого сигнала будет пропорциональна f²(_i). Энергия принимае­мого сигнала тогда будет пропорциональна f⁴(_i). Если через Э₀ обозначить энер­гию принимаемого импульса в случае, когда ось антенны направлена на цель, то энергия i-го импульса пачки равна

. (22)

Модуль корреляционного интеграла пропорционален амплитуде сигнала, тогда

, (23)

Z_0i - модуль корреляционного интеграла, который вырабатывался, если бы цель была на оси антенны.

Таким образом, зависимость Э_i и Z_i от угловой координаты цели установ­лена и определяется соотношениями (22) и (23).

Рассмотрим теперь пачку импульсов. Так как шумы, действующие в мо­менты приёма импульсов пачки, независимы, то многомерные плотности вероят­ностей выборочных данных, для пачки импульсов определяются произведением многомерных плотностей для отдельных импульсов. Тогда отношение правдопо­добия для пачки импульсов определяется произведением отношений правдопо­добия для отдельных импульсов.

Для некогерентных пачек случайные амплитуды и фазы импульсов (или только фазы, если цель нефлюктуирующая) независимы. В этом слу- чае усреднение по ним отношения правдоподобия для пачки импульсов сво­дится к усреднению отношения правдоподобия для каждого отдельного импульса пачки.

Тогда отношение правдоподобия для пачки импульсов, усреднённое по случайным амплитудам и фазам, можно записать

, (24)

_i - отношение правдоподобия для i-го импульса пачки, определяемое (21) или (22) соответственно, для случая нефлюктуирующей и флюктуирующей цели, m -число импульсов в пачке.

Если учесть зависимость Э_i и Z_i от угловой координаты цели, определяемую (22) и (23), то отношение правдоподобия для нефлюктуирующей пачки импульсов со случайными начальными фазами

(25)

для флюктуирующей пачки со случайными начальными фазами

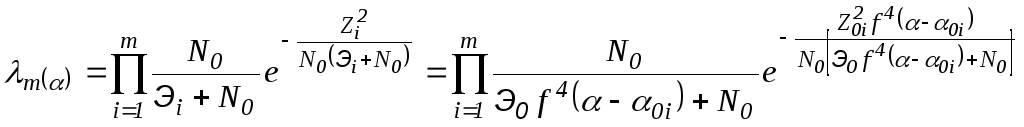. (26)

Для отыскания оценок максимального правдоподобия необходимо на основании полученных с выхода приёмника значений модулей корреляционного интеграла Z_0i (i= 1, ... m) сформировать функции (25) и (26) и найти значение , при котором они достигают максимума. Так как логарифмическое преобразование монотонно, отыскание max_m() эквивалентно отысканию maxln_m(). Логарифмируя (25) и (26), получаем

, (27)

. (28)

Если диаграмма направленности антенны f() симметрична относительно оси антенны и наблюдение проводится при угловых положениях оси антенны, расположенных симметрично относительно истинной угловой координаты цели, то первые суммы в (27) и (28) являются постоянными величинами, независящими от  . Однако, поскольку координаты антенны, при которых проводятся наблюдения, расположены случайным образом относительно истинной угловой координаты цели, то можно сказать, что лишь в среднем значение этих сумм не зависит от угловой координаты цели. Примем в дальнейшем, что эти суммы не зависят от угловой координаты цели. Проистекающая отсюда ошибка становится заметной, если число импульсов в пачке мало (m<10).

Дифференцируя (27) и (28) по  для отыскания максимума правдоподобия, получаем уравнение максимального правдоподобия

, (29)

, (30)

Значения , удовлетворяющие (29) и (30), являются оценками максимального правдоподобия соответственно для нефлюктуирующей и флюктуирующей пачек импульсов.

Рассмотрим сначала первое уравнение (20). Если амплитуды импульсов достаточно большие или малые, алгоритм измерения может быть упрощён при использовании аппроксимации

, (31)

В случае сильных сигналов уравнение (29) эквивалентно уравнению

, (32)

где

.

Для слабых сигналов уравнение (29) принимает вид

, (33)

где

.

Для флюктуирующей пачки импульсов уравнение (30) можно представить

, (34)

,

здесь

Аналитически выразитьиз уравнения (32)-(34) не удаётся. Можно использовать алгоритмы численного решения уравнений на ЭВМ. Подбором весовая функция (W) надлежащим образом связывается с наблюдениями. Вид весовых функций в уравнениях (32) - (34) определяется заданием диаграммы направленности антенны f() и отношением сигнал/шум –q₀². На рис.15 приведены весовые функции W для сильных и слабых сигналов при нефлюктуирующей и флюктуирующей пачках импульсов. Анализ весовых функций показывает, что наиболее информативными для измерения азимута являются импульсы тех участков пачки, где крутизна её огибающей велика. Рассмотренная ранее схема фиксации начала и конца пачки наиболее близка к оптимальной при сильном сигнале для флюктуирующей пачки (два острых пика весовой функции на рис. 15).

Если пренебречь неравномерностью вращения антенны (за счёт ветровой нагрузки) и считать число импульсов в пачке большим (m>20), период повторения постоянным, то оценка угловой координаты будет иметь смысл временного запаздыванияя центра пачки относительно начала отсчёта угла (рис. 16).

(35)

Запаздывание максимума огибающей пачки можно фиксировать на выходе фильтра междупериодной обработки (рис.17, выход сумматора) с антисимметричной весовой функциейW(). При последовательном прохождении пачки из m импульсов на выходе фильтра наблюдается отклик, состоящий из (2m-1) импульсов (риc.17). При появлении m-го импульса отклик будет минимальным.

Положение максимума огибающей пачки фиксируется с точностью до периода повторения РЛС. Следует отметить, что нуль на выходе сумматора фиксируется в момент , гдеt₀ - время задержки в схеме обработки. Поправка на величину t₀ может быть учтена в вычислительном устройстве вторичной обработки. Ключевая схема пропускает на выходе импульсы, фиксирующие центр пачки, только при условии превышения порога в канале обнаружения.

Если число импульсов в пачке невелико и угловые перемещения антенны в промежутках между импульсами неодинаковы, то целесообразно вычислять текущие значения весовой функции W(_i-_оц), _i - угловое положение луча при излучении (приёме) i-го импульса, _оц -угловая координата, соответствующая текущему центру весового окна. На рис. 18 представлена упрощённая функциональная схема определения центра пачки из пяти импульсов с вычислением текущих значений весовой функции.

Продетектированные сигналы с выхода приёмника подаются на амплитудно-временной квантователь (АВК), где осуществляется временная дискретизация и многоуровневое квантование по амплитуде. Квантованные значения (модуля корреляционного интеграла) каждой точки дальности в виде многоразрядного кода записываются в ячейки многоразрядного регистра сдвига. Каждый из регистров сдвига РС₁– i рассчитан на r точек дальности, укладывающихся в периоде повторения. Число регистров сдвига РС₁ – i на один меньше, чем число импульсов в пачке ( m -1=4). Коды текущего углового положения антенны поступают с выхода датчика углового кода (ДУК) и записываются в аналогичную цепочку многоразрядных регистров РС₂ - i (рис.18). На выходах вычитателей формируются разностные значения угловых кодов текущего положения центра весового окна (выход регистра РС₂-2) и значений угловой координаты луча в предыдущих и последующих периодах повторения. Далее вычисляются значения весовой функции W_i и формируется весовая сумма

.

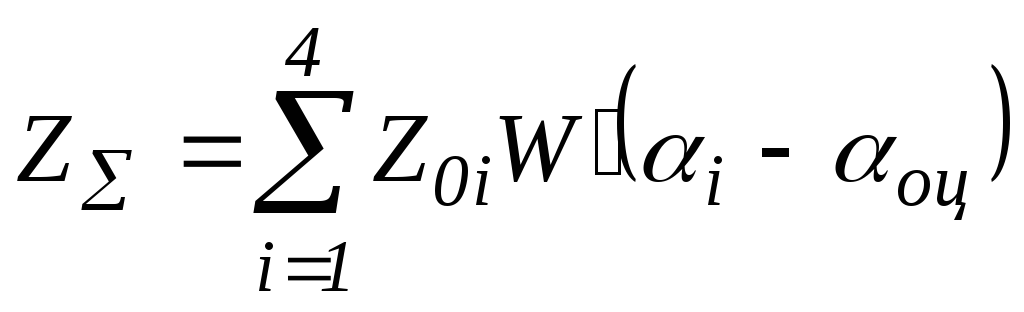Значения весовой функцииW могут вычисляться, например, табличным способом с использованием постоянных запоминающих устройств (ПЗУ). Поскольку весовая сумма Z_ - выходной отклик - вычисляется лишь в дискретных точках _i, то значение её (особенно при малом числе импульсов в пачке) изменяется скач

ками. Нуль на выходе сумматора, соответствующий значению центра пачки, зафиксирован быть не может. Лучшее, что можно сделать, это зафиксировать момент изменения знака весовой сутммы Z_. Для формирования оценки угловой координаты центра пачки необходимо использовать метод интерполяции. Аппроксимируя выходной отклик Z_ вблизи нулевого значения линейной функцией (рис.19), можно получить значение оценки по двум значениям Z_i и Z_i+1 , вычисленных при текущих положениях угла _i и _i+1

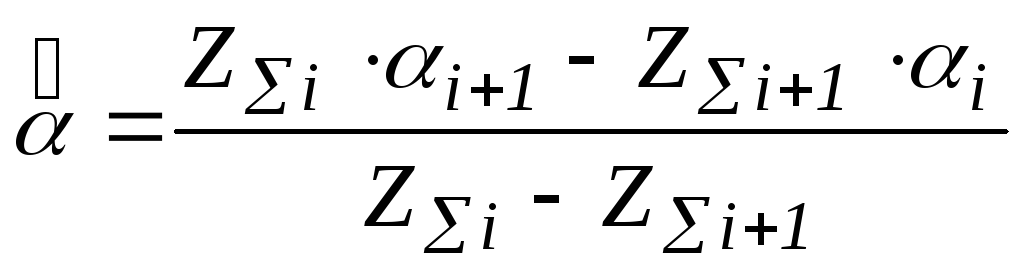. (36)

Для реализации (36) на выходе сумматора необходимо запоминать значение Z_i на период повторения. Для этой цели служит регистр РС₀. Отсчёты Z_i подаются с выхода регистра РС₀ и с выхода сумматора на схему интерполяции. Туда же подаются угловые коды _i и _i+1 - центра весового окна и центра весового окна, задержанного на период - с выходов РС₂-2 и РС₂-3. Значение оценки поступает на выход схемы (через ключ КЛ) при условии превышения порога в канале обнаружения. Анализ структурной схемы показывает, что оптимальная обработка пачки импульсов требует реализации весового суммирования на скользящем весовом окне, равном длительности пачки. С учётом большого числа точек дальности реализация оптимального измерителя угловой коррдинаты по центру пачки часто требует большого объёма памяти. На практике применяют квазиоптимальную обработку пачки импульсов [3]. В заключение следует отметить, что принципиально угловую "окраску", позволяющую осуществить измерение угловой координаты, даёт не только вращение антенны, но и перемещение её в пространстве. Пусть источник излучения (цель) неподвижен, а приёмная антенна движется вдоль оси x со скоростью V, причём ось антенны при этом остаётся перпендикулярной к этой оси (рис. 20). Тогда за период повторения антенна сместится на расстояниеx=VT. Расстояние антенны до источника излучения увеличится на R=xsin. Дополнительный сдвиг фазы высокочастотного заполнения импульса, обусловленный перемещением антенны за период Т, равен

. (37)

Амплитуда принятого импульса при движении антенны практически остаётся неизменной, так как R<<R, где R - дальность до источника излучения. Угловая окраска будет чисто фазовой, так как _T зависит от угла. Таким образом, если при вращении луча информацию об угловом положении источника извлекали за счёт сравнения амплитуд принимаемых импульсов, то при перемещении антенны угловая информация может быть извлечена из сравнения фаз импульсов. Для реализации одноканального метода сравнения фаз необходимо сохранение когерентности принимаемых сигналов в течение времени перемещения антенны. На практике это осуществить значительно труднее. Для движущихся целей _T является функцией векторов скоростей движения излучателя и антенны. В этом случае задача ещё более усложняется. Специальные методы обработки, использующие фазовую окраску сигнала, применяются в бортовых РЛС с синтезированной апертурой [1].