
Мет. указ. к лаб. раб. по ЭП / Л.р.8 - Момент инерции
.pdf
Экспериментальное определение момента инерции электромашинного агрегата |
-11- |
|
|
E K |
= J × w2 |
, |
(4) |
|
2 |
|
|
где J – момент инерции привода, кг×м2; w - угловая скорость, рад/с.
Очевидно, что энергия, запасенная приводом, при самоторможении бу- дет израсходована на преодоление потерь вращения за период (время) тор- можения.
Выражение (4) дает возможность определить момент инерции привода:
J = |
2 × E K |
= |
2 × A |
. |
(5) |
w2 |
|
||||
|
|
w2 |
|
||
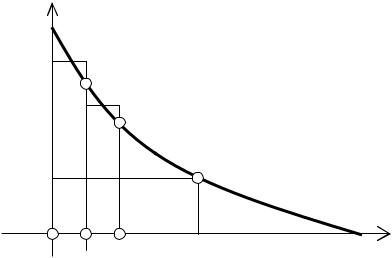
Для определения работы, затраченной на преодоление потерь вращения за время самоторможения, опытным путем снимают кривую свободного вы- бега w = f(t) и кривую зависимости потерь вращения от скорости DРВР = f(w) (соответственно кривые 1 и 2 на рисунке 4).
|
ω |
рад/с |
|
|
ω1 |
|
|
|
2 |
|
|
|
ω i |
|
|
|
|
|
1 |
РВР |
|
|
t |
Вт |
РВР i |
t i |
с |
Рисунок 4 – Зависимости w = f(t) и DРВР = f(w)
По этим кривым строят зависимость потерь вращения от времени DРВР = f(t) (рисунок 8).
Так как t – время торможения, с; а DРВР – потери вращения, Вт, то пло- щадь, заключенная между кривой DРВР = f(t) и осями координат, будет рав- няться работе А. Эту площадь можно определить, заменив кривую DРВР = f(t) на ступенчатый график (см. рисунок 5). Тогда работа определится выражени- ем:
|
a + b |
|
b + c |
|
|
|
|
A = Dt × |
|
+ |
|
+ ... , Дж, |
(6) |
|
|
|
||||
|
2 |
|
2 |
|
|
|
где |
Dt – отрезок времени, с; |
|
|
|
|
|
a, b, c … – соответствующие ординаты, Вт.
Если опыт свободного выбега проводится не до полной остановки приво- да, а от скорости w1 до скорости wK, т.е. снимают только части кривых w = f(t) и DРВР = f(w), то формула для определения момента инерции примет вид:
-12- |
Методические указания к лабораторной работе № 7 |
|
|
|||
|
|
|
|
|
|
|
|
J = 2 × |
|
A ~ |
, кг×м2, |
(7) |
|
|
w2 |
- w2 |
||||
|
|
|
|
|
||
|
|
1 |
K |
|
|
|
где |
А~ – работа, определяемая площадью, заключенной между частью |
|||||
|
кривой (рисунок 8), осями координат и вертикалью, проведенной |
|||||
|
через точку, соответствующую скорости wK. |
|
|
|||
РВР  Вт
Вт
a b c |
ω k |
РВР k
t
0 t |
t k |
с |
Рисунок 5 – Зависимости DРВР = f(t)
Для определения потерь вращения DРВР двигателя постоянного тока с не- зависимым возбуждением вычисляют мощность холостого хода и потери в
меди по формулам: |
|
|
|
|
|
|
|
P0 |
= U × I0 , Вт; |
(8) |
|||
|
DP |
|
= I2 ×R |
Я |
, Вт, |
(9) |
|
МЕД |
0 |
|
|
||
где |
U – напряжение на зажимах якоря двигателя, В; |
|
||||
|
I0 – ток якоря при холостом ходе привода, А; |
|
||||
|
RЯ – сопротивление якоря общее, Ом. |
|
||||
Общее сопротивление якоря определяют по формуле: |
|
|||||
|
R Я = 1,2 ×(R ОЯ + R ОДП + R КО ) + R ЩК , |
(10) |
||||
где RОЯ – сопротивление обмотки якоря, Ом;
RОДП – сопротивление обмотки дополнительных полюсов, Ом; RКО – сопротивление компенсационной обмотки, Ом;
RЩК – сопротивление щеточного контакта, Ом;
1,2 – коэффициент приведения сопротивлений к нагретому состо- янию (в случае класса изоляции В).
Если сопротивления обмоток якоря, добавочных полюсов и компенсаци- онной обмотки приведены в справочнике уже для нагретого состояния, то при расчете сопротивления якорной цепи следует вместо коэффициента 1,2 использовать коэффициент равный 1.
У двигателей небольшой мощности компенсационная обмотка может от- сутствовать, тогда при расчете сопротивления якорной цепи в формуле (10) следует положить RКО = 0.
Экспериментальное определение момента инерции электромашинного агрегата |
-13- |
|
|
Сопротивление щеточного контакта определяется по формуле:
R ЩК |
= |
UЩ |
, |
(11) |
|
||||
|
|
IЯном |
|
|
где DUЩ – падение напряжения на щеточном контакте, В; ( UЩ= 0,6 В –
для медно-графитовых щеток, UЩ = 2 В – для графитовых щеток);
IЯном – номинальный ток якоря двигателя, А.
В случае если в справочнике не заданы сопротивления обмоток двигате- ля, то сопротивление якорной цепи можно оценить по приближенной форму- ле, считая, что половина всех потерь в двигателе приходится на долю пере- менных потерь:
R Я |
= |
1 |
× |
UЯном |
×(1- hНОМ ) ; |
(12) |
|
|
|||||
|
2 |
|
IЯном |
|
||
Из формул (8) и (9) следует, что: |
|
|||||
|
DPВР = P0 - DPМЕД , Вт |
(13) |
||||
Потери вращения вычисляют для каждого измерения скорости, после че- го по полученным данным строят зависимость DРВР = f(w).
Изложенный метод определения момента инерции чаще всего применя- ется для двигателей постоянного тока.
Метод падающего груза
Применение этого метода наиболее целесообразно для двигателей с не- большими потерями вращения, что имеет место в асинхронных машинах с подшипниками качения.
Экспериментальное определение момента инерции методом падающего груза проводят следующим образом: На шкив с радиусом R наматывается не- сколько витков шнура, на конце которого подвешивается груз G. Падая с за- ранее известной высоты h, он сообщает вращающимся частям угловое уско- рение.
Зная вес груза G, высоту падения h и время падения t, нетрудно опреде- лить момент инерции J или маховый момент GD2 исследуемого двигателя.
При определении J или GD2 исходят из следующих соображений: при не- подвижном роторе или при движении ротора с установившейся скоростью
под действием груза момент на валу электродвигателя равен: |
|
M = G × R , Н×м, |
(14) |
где R – радиус шкива, м. |
|
Если же движение под действием груза происходит с ускорением, то часть силы тяжести груза идет на сообщение ускорения самому грузу:
|
|
m × |
dV |
= |
G |
× |
dV |
, |
|
|
|
|
|
|
(15) |
|||||
|
|
dt |
g |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|||||||
а часть – на угловое ускорение (dw/dt) ротора с маховыми массами |
|
|||||||||||||||||||
|
dV |
|
|
G |
|
|
dV |
|
|
|
|
|
1 |
|
dV |
|
|
|
||
G - m × |
= G - |
× |
= G × 1 |
- |
× |
|
, |
(16) |
||||||||||||
|
|
|
|
|
||||||||||||||||
|
dt |
|
|
g |
|
dt |
|
|
|
|
g |
|
dt |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||

-14- |
Методические указания к лабораторной работе № 7 |
|
|
при этом потерями вращения пренебрегаем.
В свою очередь динамический момент сопротивления привода равен:
M ДИН |
= J × |
dw |
. |
(17) |
|
||||
|
|
dt |
|
|
Теперь, исходя из того, что крутящий момент и момент сопротивления на валу электродвигателя равны, запишем:
G × 1- |
1 × dV |
× R = J × dw , |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
||||||||||
|
|
|
g dt |
|
|
|
|
|
|
||||||||||||||
а так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w = |
V |
, |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
dV |
|
|
|
|
dV |
|
1 |
|
|||||||||||
G × 1- |
|
× |
× R = J × |
× |
. |
||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
g |
|
|
|
|
|
|
|
|
|
dt |
|
|
|
R |
||||||||
|
|
|
dt |
|
|
|
|
|
|
|
|||||||||||||
Откуда получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||
J = R |
|
×G |
× |
|
|
|
- |
|
|
|
|
. |
|||||||||||
|
|
|
|
|
g |
||||||||||||||||||
|
|
|
|
|
|
|
dV |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|||||||
(18)
(19)
(20)
(21)
Так как движение происходит под действием постоянной силы, создава- емой грузом, то имеет место равномерно-ускоренное движение, величина ускорения которого равна:
|
|
a = |
V |
, |
|
|
|
|
|
|
(22) |
|||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
t |
|
|
|
|||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
V = a × t + C1 . |
|
|
(23) |
|||||||||||||
А так как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
V = |
dh |
, |
|
|
|
|
(24) |
|||||||||
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|||||||
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a × t + C |
|
|
= |
dh |
. |
|
|
(25) |
|||||||||
|
1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
h = |
a × t 2 |
+ C × t + C |
|
, |
(26) |
||||||||||||
|
|
|
2 |
|||||||||||||||
|
2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
С1 и С2 определяются из начальных условий. |
|
||||||||||||||||
При t = 0 скорость V = 0 и расстояние h = 0, тогда C1 = 0 и С2 = 0. |
|
|||||||||||||||||
Подставив С1 и С2 в выражение (26), получим: |
|
|||||||||||||||||
|
|
h = |
a × t 2 |
. |
|
|
|
(27) |
||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
Откуда: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
a = |
dV |
= |
2 × h |
. |
|
|
(28) |
||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
dt |
|
|
|
|
|
t 2 |
|
|
|
||||||
Выражение (28) подставим в (21):
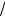
Экспериментальное определение момента инерции электромашинного агрегата |
-15- |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|||
|
|
|
J = |
R 2 ×G × |
|
× t 2 - |
|
, кг×м2. |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
2 × h |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|||||
Так как маховый момент |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
GD2 = J × 4 ×g , |
|
|
|
|
|
||||||||
а |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R = |
D |
, |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||
то |
|
× 1 × t 2 - |
1 ×4 ×g = G ×D2 × g × t |
|
||||||||||||||
GD2 = G × D |
|
|
||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
×h |
|
|
|
|
|
|
×h |
|||||||
|
4 2 |
g |
|
|
|
2 |
||||||||||||
(29)
-1 , Н×м2. (30)
Таким образом, выражения (29) и (30) позволяют, выполнив необходи- мые измерения экспериментально определить момент инерции привода и ма- ховый момент соответственно.
Если же потери вращения достаточно велики, и ими пренебречь нельзя, то поступают следующим образом: определяют величину момента трения пу- тем постепенного увеличения веса груза на шнуре до G0, т.е. до величины, когда двигатель будет находиться на грани трогания, а вес G0 будет уравно- вешивать силы трения (здесь сила трения принимается независимой от ско- рости вращения, что справедливо при малых скоростях). Зная величину силы трения можно теперь определить величину момента инерции, учтя, что мо- мент, создаваемый подвешенным грузом, расходуется не только на преодоле- ние динамического момента сопротивления, но и на преодоление момента трения, равного:
|
G |
|
dV |
|
|
|
|
|
|
|
|
dw |
|
|
|
J |
|
dV |
|
|
||||
G - |
× |
|
× R |
= G 0 |
× R + J × |
= G 0 |
× R + |
× |
, |
(31) |
||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
g dt |
|
|
|
|
|
|
|
|
dt |
|
|
|
|
R dt |
|
||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1- G |
0 |
G |
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
J = |
|
|
|
× t 2 |
- |
|
|
|
×G × R 2 . |
(32) |
|||||||||||
|
|
|
|
2 × h |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
|
|
|
|
|
||||||
Метод маятниковых колебаний
Экспериментальное определение момента инерции методом маятнико- вых колебаний заключается в следующем: с наружной поверхности шкива, на расстоянии R от оси вращения закрепляется груз весом G, нарушающий балансировку вращающихся частей. При этом размеры груза в радиальном направлении должны быть малы, чтобы в расчет не была внесена большая погрешность. Ротор или якорь выводится из положения равновесия. После этого определяется время, в течение которого он придет в состояние покоя, а также число колебаний n за этот отрезок времени.
Уравнение движения для данного случая будет иметь вид, подобный уравнению маятник:
G × R ×sin a = J × dw + G ×R |
|
× dw = J + G × R |
|
× dw |
, |
(33) |
||||||||
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
g |
|
|
dt |
g |
|
|
dt |
|
|
||
или

-16- |
|
|
Методические указания к лабораторной работе № 7 |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
G × R |
|
|
×sin a = |
dw |
= |
|
|
d 2a |
. |
(34) |
||||||||||
|
|
G × R 2 |
|
|
|
|
|||||||||||||||
|
J + |
|
|
|
|
|
|
|
|
dt dt 2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
g |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решая это уравнение, находим выражение для времени одного колеба- |
|||||||||||||||||||||
ния: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
T = 2 × p× |
|
|
J |
|
+ |
R |
, |
(35) |
|||||||||||
|
|
|
G × R |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
g |
|
|
||||||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
T |
2 |
|
|
R |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
J = |
|
- |
|
×G × R , кг×м2. |
(36) |
||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||
|
|
4 ×p2 |
|
|
g |
|
|
|
|
|
|
|
|
|
|
||||||
Метод крутильных колебаний
Этот метод заключается в следующем: ротор двигателя подвешивается на стальной проволоке и ему придается колебательное движение за счет за- кручивания проволоки. Период колебания будет зависеть от момента инер-
ции ротора: |
|
|
|
|
||
|
|
|
|
|
|
|
T = 2 ×p× |
|
J |
, |
|||
|
|
|||||
|
|
|
k |
|||
откуда |
|
|
|
|
||
J = |
T2 |
× k , кг×м2, |
||||
4 × p2 |
||||||
|
|
|
|
|
||
где k зависит от материала и размеров проволоки:
k = p× E × r 4 ,
2 ×l
где E – модуль кручения материала проволоки, r – радиус проволоки,
l – длина проволоки.
(37)
(38)
(39)
К недостаткам этого метода определения момента инерции по сравне- нию с предыдущими методами следует отнести обязательную разборку элек- тродвигателя перед проведением эксперимента.
Экспериментальное определение момента инерции электромашинного агрегата |
-17- |
|
|
Контрольные вопросы
1.На какие свойства электропривода влияет момент инерции или ма- ховый момент?
2.Как связан момент инерции и маховый момент?
3.При какой угловой скорости 100 рад/с или 200 рад/с двигатель за- пасет большую кинетическую энергию и во сколько раз?
4.Как связаны запасенная кинетическая энергия во вращающихся ча- стях привода и работа за время самоторможения?
5.Как изменится время торможения привода, если на вал двигателя установить дополнительный маховик?
6.На что тратится кинетическая энергия, запасенная вращающимися частями привода, при его самоторможении до полного останова?
7.Какие методы экспериментального определения момента инерции вам известны?
8.В чем заключается определение момента инерции методом падаю- щего груза?
9.В чем заключается метод маятниковых колебаний для определения момента инерции привода?
10.Как изменится кривая свободного выбега, если момент инерции привода увеличить в 2 раза?
11.Какие недостатки имеет метод крутильных колебаний для опреде- ления момента инерции привода?
12.Поясните, как графически получить зависимость потерь враще- ния от скорости при заданных зависимостях скорости от времени и потерь вращения от скорости.
13.Пояснить методику определения работы, затраченной приводом на преодоление потерь вращения за время самоторможения в опыте определения момента инерции методом свободного выбега.
14.Дать оценку трудоемкости определения момента инерции извест- ными экспериментальными методами.
-18- |
Методические указания к лабораторной работе № 7 |
|
|
Рекомендуемая литература
1.Москаленко В.В. Автоматизированный электропривод: Учебник для ву- зов. – М.: Энергоатомиздат, 1986. – 416 с.: ил.
2.Основы автоматизированного электропривода: Учеб. пособие для ву- зов/ М.Г. Чиликин, М.М. Соколов, В.М. Терехов, А.В. Шинянский. – М.:
Энергия, 1974. – 568с.: ил.
3.Чиликин М.Г. Теория автоматизированного электропривода: Учеб. по- собие для вузов / Чиликин М.Г., Ключев В.И., Сандлер А.С. – М.: Энер-
гия, 1979. – 616с.: ил.
