Лекции.Принят.Управ.Решений

42

предпринимателя избежание риска зачастую означает отказ от возможной прибыли.

Одной из количественных оценок степени риска при принятии УР является колеблемость (изменчивость) возможного результата

(величины выигрыша или проигрыша) xi принятия решения yi. В

статистике для оценки колеблемости используют коэффициент вариации Vi:

Vi i ,

xi

n

где i xij xi 2 pj , n – количество анализируемых состояний

j 1

«природы». В соответствии с величиной Vi различают:

-низкий уровень риска – Vi 10%,

-средний уровень риска – 10% Vi 25%,

-высокий уровень риска – Vi > 25%.

Знание степени риска в сочетании с индивидуальной функцией полезности позволяет проанализировать отношение ЛПР к риску. С

этой точки зрения всех индивидуальных ЛПР можно разделить на две группы.

Первая группа ЛПР с так называемой внутренней стратегией

определяют свои успехи и неудачи прежде всего личными качествами, способностями, волей, уровнем интеллекта и т.п. Эти лица, как правило, более активны, более целеустремленны при поиске информации в неопределенной обстановке. Они легче преодолевают трудности в сложных, меняющихся условиях, более объективны в оценке полученных результатов и выводах по ним.

Лица с внутренней стратегией чаще принимают решения со средним уровнем риска. Они в основном рассчитывают на свои силы и способности и не стремятся принимать решения, при которых

43

приходится уповать главным образом на случайность.

Вторая группа ЛПР с так называемой внешней стратегией,

напротив, исходит из того, что их поражения и победы зависят главным образом от внешней среды, на которую они не могут воздействовать.

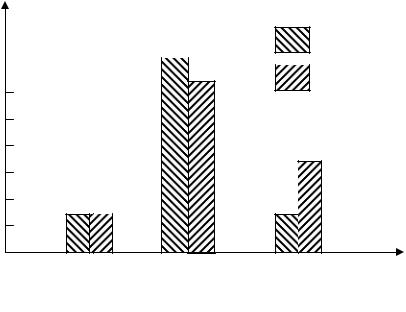
Отношение к риску лиц с внутренней (Вн) и внешней (Вш)

стратегиями показано графически на рис.8.

Относительное кол-во принимаемых

Вн

0,6

0,5

0,4

0,3

0,2

0,1

Низкий Средний Высокий

Рис. 8. Отношение к риску ЛПР

4. HW-критерий (критерий Гурвица) использует целевую

функцию вида:

а выбор оптимальной альтернативы у осуществляется по правилу:

Относится также к критериям рациональной стратегии ЛПР. При

с=1 HW-критерий превращается в ММ-критерий «пессимизма», а

при с = 0 – в критерий «оптимизма» (азартного игрока). Таким образом, множитель с является показателем соотношения

44

«пессимизма» и «оптимизма».

Условия применения HW-критерия:

- информация о вероятностях состояний «природы» отсутствует;

-количество реализаций решений ограничено;

-допускается определенная степень риска.

5. HL-критерий (критерий Ходжа-Лемана) использует целевую функцию следующего вида:

Выбор оптимальной альтернативы у осуществляется по правилу:

Коэффициент выражает степень доверия ЛПР к используемому распределению вероятностей. Если это доверие велико, то акцентируется BL-критерий, в противном случае – ММ-

критерий. Условия использования HL-критерия следующие:

- наличие предположений о распределении вероятностей pj

состояний «природы» sj ;

-решение реализуется бесконечно много раз (теоретически);

-в случае малого числа реализаций допускается определенная степень риска.

6. G-критерий (критерий Гермейера) использует целевую функцию вида:

причем значения f(yi sj) интерпретируются как значение потерь от

принятия решения yi в ситуации sj, а выбор оптимальной

альтернативы у осуществляется согласно правилу:

45

Внекотором смысле G-критерий обобщает критерий

«пессимизма», а в случае pj = const = n-1 они идентичны. Обычно используется при следующих обстоятельствах:

-задача принятия УР является одноцелевой;

-распределение вероятностей pj известно;

-допускается определенная степень риска.

Очень часто тот или иной критерий выбирается ЛПР интуитивно (особенно это касается ММ-критериев). В этом случае ЛПР рекомендуется подробно проанализировать ситуацию и постараться обосновать правильность использования критерия. Если ЛПР затрудняется в выборе того или иного критерия, целесообразно провести анализ различных критериев, определить, совпадают или различаются выбранные таким образом оптимальные варианты решений, и, в конечном счете, постараться оценить влияние критериев на выбор оптимального решения.

5.2. Случай группового принятия решения (групповой

выбор)

Групповой выбор является столь же распространенным в практике принятия решений, как и индивидуальный. Под групповым выбором понимают процедуру принятия коллективного решения на основе согласования индивидуальных предпочтений членов группы.

Примеры группового ЛПР: советы директоров, НТС, бригады проектантов, проблемные комиссии и т.п. Постановка задачи группового выбора формулируется следующим образом: для разрешения проблемной ситуации предлагается ряд вариантов решений Y y1,y2, ,ym . Имеется групповое ЛПР, состоящее из d членов. Каждый член группы может выбирать решения из

46

множества YД в соответствии со своими предпочтениями. Оценка каждого решения группой представляет собой вектор-функцию предпочтений f f1, , fd . Для образования единого группового предпочтения с целевой функцией F F f1, , fd , необходимо согласовывать индивидуальные предпочтения, что выполняется на основе принципа группового согласования П.

Логические формулы, описывающие процесс принятия УР в случае группового ЛПР, отличаются в некоторых деталях от индивидуального. Так, для индивидуального ЛПР:

S0,T,R S,Ц,Г,YД , f ,K,y ,

а для группового ЛПР:

где:

S0 – проблемная ситуация;

T – регламентное время для принятия решения;

R – ресурсы, потребные для принятия решения;

S s1, ,sn – множество гипотетических ситуаций (гипотез,

версий), доопределяющих исходную проблемную ситуацию S0 ;

Ц ц1, ,цk – множество целей, достигаемых при принятии решения;

Г 1 , , r – множество ограничений;

YД y1, ,ym – множество допустимых альтернатив;

f f yi,sj,цh – функция предпочтения индивидуального ЛПР, оценивающая последствия решения уi в ситуации sj для достижения цели цh, i 1,m , j 1,n,h 1,k;

K – критерий выбора оптимального решения у ;

47

f ( f1, , fd ) – вектор-функция группового ЛПР, где d –

количество членов группы; fp– функция предпочтения p-го члена группы, p 1,d ;F f F f1, , fd – целевая функция (функция группового предпочтения); – принцип группового согласования.

Вектор-функция группового ЛПР f может быть задана с помощью d матриц:

Рассмотрим наиболее часто используемые на практике принципы группового согласования П.

1. Принцип «диктатора». В этом случае

F f F f1, , fd fa ,

где a – номер члена-диктатора в группе. Правило выбора оптимального решения:

Обычно такой принцип используется лишь в военных организациях, и не способствует хорошему микроклимату в коллективе, если в нем отсутствуют отношения строгой подчиненности.

2. Принцип большинства голосов. Группа разбита на коалиций, c соответствующим количеством членов в каждой и функциях предпочтения f1, , f ,общих для каждой

48

коалиции. Функция группового предпочтения F равна функции предпочтения той коалиции, число членов которой больше определенного порога c:

F f1, , f fq , если nq c,

2

c 3 d – принцип 2/3 голосов. Правило выбора оптимального

решения:

3. Принцип Парето. Функция предпочтения (целевая функция) определяется как вектор, компонентами которого являются функции предпочтения членов группы:

F f1, , fd f1, , fd f.

По принципу Парето решение yi предпочтительнее yj, если все

члены группы считают, что первое решение не хуже второго и, по крайней мере, один из членов группы считает, что первое решение

Те решения, которые удовлетворяют этому условию, образуют множество Парето-эффективных решений YЭ, которые считаются оптимальными. Таким образом, оптимальное по принципу Парето решение в общем случае не единственное решение, а подмножество

YЭ YД. Все решения, входящие в это подмножество yi YЭ,

49

считаются оптимальными и являются не доминирующими и не сравнимыми.

Множество Парето-эффективных решений обладает следующими двумя свойствами, которые могут быть учтены при его построении:

если yi,yk YЭ, а yj YЭ, то:

1) f1 yi , , fd yi f1 yk , , fd yk , т.е. эквивалентны

по отношению векторного порядка и не сравнимы;

2)f1 yi , , fd yi f1 yj , , fd yj .

Врезультате использования принципа Парето исходное множество допустимых (по ограничениям) решений YД «сжимается»

до эффективного подмножества YЭ, которое может быть исследовано дальше на предмет отыскания единственного оптимального решения. Количественно степень такого «сжатия» оценивается с помощью коэффициента определенности выбора :

mД mЭ , mД 1

где mД – мощность множества допустимых решений; mЭ – мощность множества эффективных решений.

Пример. Пусть два члена группы (d = 2) со своими функциями предпочтения f1 и f2 провели оценку в баллах 4-х вариантов решений y1,y2,y3,y4 следующим образом:

Из анализа матрицы следует, что:

1)y1 не сравнимо с y2;

2)y1 y3, следовательно, y1 YЭ (по 1 и 2 свойствам);

3)y2 не сравнимо с y3;

50

4) у2 y4, т.е. y4 YЭ.

Таким образом, множество Парето: YЭ=(y2, y3).

К другим принципам группового согласования можно отнести принципы, основанные на стратегиях: суммирования рангов,

минимизации отклонений, оптимального предвидения, средних полезностей решений в условиях риска и т.д.

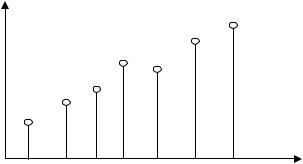
Экспериментальные исследования сравнительного отношения к риску при принятии решения по одной и той же задаче отдельным лицом и группой показали, что группа идет на риск значительно более охотно, чем отдельные личности (рис.9). Это обусловлено рядом причин: разделение ответственности за исход рискованных действий между членами группы; стремление следовать в своем выборе за лидером; нежелание оказаться более осторожным, чем другие и т.д.

Уровень

риска

Количество членов группового ЛПР

Рис. 9. Влияние состава ЛПР на отношение к риску

Эти же исследования показывают, что преимущества группового решения тесно связаны с типом решаемой задачи. Оно оказывается более эффективным при решении трудно формализуемых задач, а также задач, требующих от принимающего решения большого опыта.

51

6. МЕТОДЫ ПРИНЯТИЯ УПРАВЛЕНЧЕСКИХ

РЕШЕНИЙ В УСЛОВИЯХ НЕПОЛНОЙ

ИНФОРМАЦИИ

Эти методы используются в практике менеджмента либо при анализе не структурируемых или слабо структурируемых проблем,

либо в случае принципиальной невозможности применения способа количественной оценки последствий принимаемых решений

(например, в случаях принятия решений о замещении вакантных должностей, выбора руководителя подразделения, способов использования прибыли в акционерном обществе и т.п.)

В этих условиях могут быть рекомендованы следующие способы оценки:

- парное сравнение без предварительного ранжирования альтернатив; при использовании этого способа вначале строятся графы бинарных отношений, а затем – соответствующие им матрицы парных сравнений сij , где сij (1,5; 1,0; 0,5); при этом способе допускается нарушение свойства транзитивности;

- парное сравнение с предварительным ранжированием альтернатив; при использовании этого способа вариантам решений вначале присваиваются ранги, а затем строятся соответствующие матрицы парных сравнений сij , где сij (1,0); в этом случае нарушение свойства транзитивности автоматически исключается.

Последующее преобразование матриц сij с целью определения оптимального решения у может быть выполнено с помощью следующих методов обработки.

6.1. Метод расстановки приоритетов

Метод расстановки приоритетов (МРП) рекомендуется

использовать при способе парных сравнений без предварительного