электричество и магнетизм лабораторный практимум

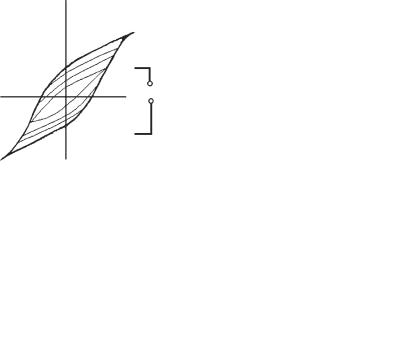
пряженности магнитного поля намагниченность магнетика становится постоянной J = const, наступает состояние насыщения и магнитная индукция B возрастает только за счет увеличения напряженности магнитного поля. Поэтому в соответствии с (2) кривая намагничения перейдет в пологий линейный участок. При последующем уменьшении напряженности магнитного поля график намагничения или график зависимости B от H не совпадает с первоначальной кривой намагничения, а соответствует на графике участку АВ (рис. 2). Когда напряженность магнитного поля H становится равной нулю, то намагничение не исчезает и характеризуется величиной B, называемой остаточной индукцией. Намагничение обращается в нуль лишь под действием внешнего магнитного поля Hc, направление которого противоположно первоначальному. Напряженность магнитного поля Hc носит название коэрцитивной силы. При дальнейшем возрастании напряженности магнитного поля, обратного по направлению, вновь достигается насыщение (точка D). Если от точки насыщения уменьшать обратное магнитное поле до нуля, а затем его увеличивать до точки насыщения A, то получится замкнутая кривая, называемая петлей гистерезиса.

Теория ферромагнетизма была разработана Я. И. Френкелем и В. Гейзенбергом. Из нее следует, что ответственными за магнитные свойства ферромагнетиков являются собственные (так называемые, спиновые), магнитные моменты электронов. При определенных условиях в кристаллах могут возникать, так называемые силы обменного взаимодействия, под действием которых спиновые магнитные моменты электронов выстраиваются параллельно друг другу. В результате возникают области самопроизвольного или спонтанного намагничения, которые называются доменами. При отсутствии внешнего магнитного поля векторы магнитных моментов отдельных доменов ориентированы в пространстве хаотически, так что результирующий магнитный момент ферромагнетика равен нулю. Внешнее магнитное поле, в которое помещается ферромагнетик, ориентирует магнитные моменты не отдельных молекул, как в случае парамагнетиков, а целых областей спонтанной намагниченности.

Коэрцитивная сила характеризует свойство ферромагнетика сохранять намагниченность и, наряду с относительной магнитной проницаемостью, определяет возможности его применения для тех или иных практических целей. Большой коэрцитивной силой обладают углеродистые, вольфрамовые и хромовые, алюминиево-никелевые и другие стали. Эти

31

материалы дают широкую петлю гистерезиса, и называются “твердыми” магнитными материалами. Из них изготавливаются постоянные магниты. К “мягким” магнитным материалам, обладающим малой коэрцитивной силой, относятся: “мягкое” железо, сплавы железа с никелем. Эти материалы используются для изготовления сердечников трансформаторов.

Перемагничивание ферромагнетика связано с поворотом векторов намагничения доменов на 360°. Работа, необходимая для этого, совершается за счет энергии внешнего магнитного поля. Количество тепла, выделяющегося при перемагничивании, пропорционально площади петли гистерезиса.

Нарушение преимущественной ориентации векторов намагничения доменов может быть вызвано ударом или нагреванием ферромагнетика. С повышением температуры остаточная намагниченность ферромагнетика уменьшается и при некоторой температуре, называемой точкой Кюри, исчезает полностью. Это объясняется тем, что тепловое движение молекул ферромагнетика становится столь интенсивным, что области спонтанной намагниченности распадаются. При температурах, которые выше точки Кюри, ферромагнетик во внешнем магнитном поле ведет себя как парамагнитное вещество. Он не только теряет свои ферромагнитные свойства, но и изменяет теплоемкость, электропроводность и некоторые другие физические характеристики.

Упражнение 1

Исследование магнитного гистерезиса с помощью электронного осциллографа

Описание лабораторной установки. Исследуемый ферромагнетик имеет форму тороида (рис.3), на который намотаны две обмотки. При протекании по первичной обмотке тока I1 внутри обмотки возникает магнитное поле. Ферромагнетик намагничивается и добавочное магнитное поле усиливает внешнее. Для определения напряженности магнитного поля, создаваемого внутри тороида первичной обмоткой, воспользуемся известной формулой

где N1 – число витков первичной обмотки; l – длина средней линии внутри тороида. Если первичную обмотку тороида подключить к ис-

32

точнику переменного напряжения, то в ней возникает переменный ток

I = I0 sin ω t,

Напряженность магнитного поля внутри тороида будет изменяться по тому же закону, что и ток в первичной обмотке. Поэтому падение напряжения на сопротивлении R1, включенном последовательно в цепь вторичной обмотки, будет пропорционально напряженности магнитного поля внутри тороида H.

Переменное магнитное поле, создаваемое током первичной обмот-

где Ф = BS – поток магнитной индукции, пронизывающий каждый из витков вторичной обмотки; S – площадь витка; N2 – число витков вторичной обмотки.

Если концы вторичной обмотки подсоединить к интегрирующей цепочке, состоящей из последовательно соединенных сопротивления R2 и конденсатора C2, и удовлетворяющей условию R2 >>1/(ω C2) (рис. 3), то напряжение U2 на обкладках конденсатора C2 будет изменяться пропорционально величине магнитной индукции поля, пронизывающего витки вторичной обмотки. Действительно, сила тока в цепи вторичной обмотки

где Z – полное сопротивление цепи вторичной обмотки; L2 – индуктивность вторичной обмотки. При незначительной величине индуктивности L2 и при R2 >> 1/(ω C2) будем иметь Z ≈ R 2 и

33

Из (9) и (10) следует очевидное равенство

Преобразуем равенство (11) и проинтегрируем полученное выражение

Подставим в (12) величину ЭДС (7) и, произведя интегрирование, получим

Если напряжение u2, пропорциональное магнитной индукции B, подать на вертикально отклоняющие пластины электронного осциллографа, а на горизонтально отклоняющие пластины подать напряжение u1, пропорциональное напряженности магнитного поля H, то луч на экране осциллографа будет описывать кривую зависимости u2 от u1, т. е. функциональную зависимость B от H в некотором масштабе. Последовательно увеличивая ток в первичной обмотке, можно получить семейство кривых, изображенных на рис. 4. Соединяя точки семейства кривых, имеющих максимальные и минимальные ординаты, получим основную кривую перемагничивания ферромагнетика (петля гистерезиса).

Порядок выполнения работы. 1. Включить осциллограф С1–77 и звуковой генератор Г3-56/1. Правый тумблер синхронизации по “х” (“Ка- нал–2”) на передней панели осциллографа поставить в нижнее положение. Рукоятками “↔ ” и “ " ” вывести сфокусированное пятно в центр сетки на экране. Наружную рукоятку переключателя “ В /дел.” (“Ка- нал–1”) поставить в крайнее положение по часовой стрелке; внутреннюю рукоятку – в положение “0,05” или “0,01”. Это будет означать, что напряжение U = 0,05 или 0,01 В, подаваемое на вертикально отклоняющие пластины, вызывает отклонение луча по вертикали на одно большое деление. Вход “время/дел.” не используется. Подключить к лабораторному макету осциллограф в соответствии со схемой (рис. 3). Напря-

34

жение с гнезд “х” лабораторного макета подается на клеммы “Внешн. синхр.” (положение “земля” и “1:1”), расположенные на правой боковой стенке осциллографа. Напряжение с гнезд “у” лабораторного макета подается на вход “Канал–1”, В/дел. (вертикально отклоняющие пластины “у”).

2. С клемм генератора звуковой частоты подается максимальное напряжение на гнезда лабораторного макета “ЗГ”. Рукоятки на передней панели генератора устанавливаются в следующие положения:

–шкала вольтметра – 63,2 В;

–внешняя нагрузка – 600 Ом;

–предел шкалы вольтметра – 30 В;

–частота в пределах (30–40)·102 или (140–170)·103 Гц;

–регулятор выхода – против часовой стрелки до отказа;

–внутренняя нагрузка “выкл”.

При сборке схемы обратить внимание на правильное присоединение проводов заземления.

35

3. Вращая по часовой стрелке рукоятку “регулятор выхода” звукового генератора, добиться получения петли гистерезиса, имеющей максимальную площадь на экране осциллографа. Пользуясь координатной сеткой, нанесенной на экран, определить координаты “у” вершин петли гистерезиса (отсчеты производить в больших делениях и их долях). Уменьшая (той же рукояткой) напряжение, подаваемое с выхода звукового генератора на вход лабораторного макета, можно получить 8–10 петель гистерезиса, записывая каждый раз координаты правой вершины кривой. Перед каждым измерением, повернув “регулятор выхода” до отказа против часовой стрелки, убеждаются в том, что световое пятно находится в центре сетки. При необходимости рукоятками “↔ ” и “" ” восстановить центральное положение пятна. Измерить число делений, соответствующих коэрцитивной силе Hс. Все результаты измерений занести в табл. 1.

Таблица 1

Вычисление результатов и оформление отчета. Вычислить в воль-

тах координаты вершин всех полученных петель гистерезиса по формулам

где α x = 4,1 В; α y = 0,05 В (или 0,01 В) – чувствительность усилителей каналов горизонтального и вертикального отклонения луча осциллографа; nx и ny – координаты вершин кривой гистерезиса х и у в больших делениях сетки осциллографа.

Подсчитать максимальные значения напряженности и индукции магнитного поля для каждой петли гистерезиса по формулам

где N1= N2 =23 витка; l – длина средней линии тороида (диаметр сред-

ней линии равен 8 мм); R1 = 73,0 Ом, R2 = 10,0 Ом, C2= 2,5·10–7 Ф; S –

площадь поперечного сечения ферромагнитного сердечника 10–5 м2. По расчетным значениям Bi и Hi построить основную кривую намаг-

ничивания B = f(H). Построить график зависимости µ= f(H).

36

Определить коэрцитивную силу ферромагнетика по формуле

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1.Какие виды магнетиков существуют в природе?

2.Какова физическая природа ферромагнетиков?

3.Дайте объяснение основной кривой намагничивания и петли гистерезиса.

4.Объясните принципы получения на экране осциллографа петли магнитного гистерезиса.

Упражнение 2

Исследование магнитного гистерезиса с помощью баллистического гальванометра

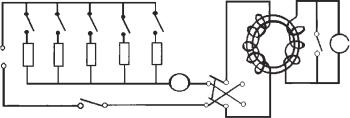
Описание лабораторной установки. Электрическая схема лаборатор-

ной установки для получения петли гистерезиса с помощью баллистического гальванометра приведена на рис. 5. Основным элементом схемы является ферромагнитное кольцо или тороид. На тороид намотаны две обмотки, играющие роль первичной и вторичной обмоток трансформатора. Через штепсельный реостат первичная обмотка подсоединяется (при помощи ключа П1) к источнику постоянного напряжения u0. Ток первичной обмотки измеряется амперметром А. Переключатель П2 служит для изменения направления тока в цепи первичной обмотки. Баллистический гальванометр включен в цепь вторичной обмотки. Демпфирование (успокоение) баллистического гальванометра произво-

Г

u0

Рис. 5

37

дится при помощи ключа П3, закорачивающего цепь рамки гальванометра. C принципом действия баллистического гальванометра следует ознакомиться в лабораторной работе № 1.

При протекании электрического тока в цепи первичной обмотки внутри ферритового кольца возникает магнитное поле, напряженность которого

где N1 – число витков первичной обмотки; l – длина тороида; I – сила тока в цепи первичной обмотки. Индукция магнитного поля и магнитный поток через поперечное сечение тороида S по определению

Изменяя ток через первичную обмотку при помощи штепсельного реостата R, тем самым изменим и магнитный поток, пронизывающий поперечное сечение ферромагнитного тороида

Отсюда следует, что для построения петли гистерезиса методом последовательного перехода от одной точки к другой необходимо изменять ток в первичной и намагничивающей обмотках, каждый раз находя изменение магнитной индукции ∆ B от предыдущего зафиксированного значения

При этом напряженность магнитного поля следует вычислять по формуле (17), сняв показание амперметра. Изложим метод определения ∆ Ф (а, тем самым, и ∆ B ).

Изменение тока в первичной обмотке и, следовательно, изменение магнитного потока (19), приводит к возникновению ЭДС индукции во вторичной обмотке. Вследствие этого через баллистический гальванометр пройдет кратковременный электрический ток

38

где N2 – число витков вторичной обмотки; Rг – сопротивление электрической цепи гальванометра. При протекании тока через рамку баллистического гальванометра, расположенную между полюсами постоянного магнита, возникает момент пары сил. Рамка с током поворачивается вместе с закрепленным на ней зеркальцем. Поворот зеркальца приводит к отклонению светового указателя (“зайчика”). В баллистическом гальванометре аппаратным способом реализуется интегрирование импульса тока (21) по времени. В результате определяется величина заряда, прошедшего через рамку гальванометра,

При малых углах поворота рамки β отклонение светового указателя на шкале баллистического гальванометра практически пропорционально величине угла поворота, а значит и величине заряда q, прошедшего через рамку. В этом случае можно положить

где C – баллистическая постоянная; ∆ n – число делений, на которое отклонялся световой указатель. Из (20), (22) и (23) находим

При помощи штепсельного реостата R ток в первичной обмотке изменяется дискретно от начального значения I0 = 0 ( H0= 0, B0= 0).

Если от начального значения тока I0 = 0 произведено m дискретных изменений силы тока ∆ Ik, то магнитная индукция в конце опыта определится суммой дискретных изменений

где γ – коэффициент пропорциональности; ∆ nk – число делений, на которое отклоняется “зайчик” на шкале баллистического гальванометра при k-м изменении силы тока. Величина напряженности магнитного поля Hm в опыте m определяется по измеренному току в данном опыте по формуле (17).

39

Порядок выполнения работы. Перед началом выполнения работы производится полное размагничивание исследуемого тороида при помощи дросселя, включенного в сеть. При этом предварительно отключают баллистический гальванометр (замыкают ключ П3) и источник постоянного напряжения (ключ П1). После размагничивания ключом П3 размыкают соответствующие контакты, переключатель П2 устанавливают в одно из рабочих положений. Ключом П1 подсоединяют схему к источнику постоянного напряжения u0. При этом все выключатели штепсельного реостата R должны находиться в разомкнутом положении. Затем включают осветитель баллистического гальванометра, и фиксируют положение светового указателя (“зайчика”) на шкале предпочтительно в нулевом положении.

Выполнение измерений начинают с включения одного сопротивления штепсельного реостата. Тем самым замыкают цепь первичной обмотки. Фиксируют количество делений, на которое отклонился “зайчик” по шкале баллистического гальванометра, и записывают показания амперметра. При этом силу тока и напряженность магнитного поля следует считать положительными. Измеренные значения величины отклонения “зайчика” ∆ n1 и силы тока I1 заносятся в табл. 2. Для того чтобы быстрее вернуть “зайчик” в первоначальное положение, замыкают ключ П3 (“успокаивают” гальванометр). После того, как “зайчик” установится в первоначальном положении, ключ П3 размыкают и включают второе сопротивление реостата. При этом также фиксируют отклонение “зайчика” ∆ n2 и измеряют силу тока в первичной обмотке I2. При вычислении магнитной индукции B2 по формуле (25) при двух включенных сопротивлениях реостата следует брать сумму двух отклонений “зайчика” в формуле (25). В то же самое время при вычислении напряженности магнитного поля H2 величину силы тока в формуле (17) следует положить, равной I2. Для определения последующих точек на всем участке кривой намагничения 0A (рис. 2) поступают аналогичным образом.

При определении значений напряженности магнитного поля и магнитной индукции на участке AB петли гистерезиса сопротивления реостата выключаются последовательно в обратном порядке. Отклонения “зайчика” баллистического гальванометра от первоначального положения следует считать отрицательными, а значения силы тока через первичную обмотку – положительными. Поэтому сумма значений ∆ nk в формуле (25), приобретает смысл алгебраической суммы.

40