электричество и магнетизм лабораторный практимум

Таким образом, отношение в левой части равенства (8) равно комплексному сопротивлению, и называется импедансом. Импеданс колебательного контура будем обозначать

Активным сопротивлением колебательного контура называется действительная часть импеданса Re (Z) = R. Реактивным сопротивлением называется мнимая часть импеданса

Реактивное сопротивление – разность индуктивного и емкостного сопротивлений.

В экспоненциальной записи импеданс колебательного контура име-

Модуль Z0 импеданса называют полным сопротивлением колебательного контура на частоте ω . Аргумент ψ импеданса равен разности фаз колебаний вынуждающей ЭДС и силы тока в контуре (это следует из определения импеданса (8); напомним, что аргумент отношения двух комплексных чисел равен разности аргументов делимого и делителя). Из (8) также следует, что амплитуда силы тока связана с амплитудой ЭДС соотношением

Полное сопротивление колебательного контура (11) минимально при равенстве нулю реактивного сопротивления

11

Равенство (14) является условием резонанса в цепи колебательного контура. Циклическая частота, определяемая при решении уравнения (14), называется резонансной частотой

Резонансная частота ω р не зависит от активного сопротивления контура, и совпадает с частотой незатухающих колебаний ω 0. При стремлении частоты ω, вынуждающей ЭДС к резонансной частоте ω р, амплитуда тока резко возрастает, и на резонансной частоте достигает максимального значения

При этом разность фаз ψ становится равной нулю. Резкое возрастание амплитуды тока при стремлении ω к ω р называется явлением резонанса, а кривая зависимости I0 от ω – резонансной кривой.

На рис. 1 приведены резонансные кривые для трех значений сопротивления колебательного контура R1<R2<R3. Резонанс выражен тем отчетливее, чем меньше активное сопротивление контура, т. е., чем меньше энергетические потери на джоулево тепло. Характерный параметр резонансной кривой – ее ширина на уровне, соответствующем половине максимальной мощности (рис. 2)

12

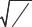
Можно показать, что

Избирательные свойства колебательного контура зависят от “остроты” резонансной кривой. О форме этой кривой можно судить по ее относительной ширине ∆ω /ω р (или по обратной величине Q).

Важная характеристика колебательной системы – добротность. Эта величина не зависит от режима вынужденных колебаний (от приложенной к контуру ЭДС ε ). Свободные колебания системы (случай ε = 0) являются затухающими вследствие потерь на джоулево тепло. При этом средняя за период энергия колебаний E экспоненциально убывает, а, отношение ∆ E/E остается неизменным (здесь ∆ E = E(t+T) – E(t); T – период колебаний). Добротность контура Q характеризуют обратной величиной E /∆ E

Итак, добротность контура Q показывает, во сколько раз запасенная в контуре энергия превосходит среднюю энергию, теряемую за один период колебаний. Добротность – величина безразмерная.

B теории колебаний доказывается, что добротность может быть найдена по ширине резонансной кривой (17)

(это соотношение выполняется с большой точностью в случае, когда

где ρ = L C – величина, называемая волновым сопротивлением контура.

Описание лабораторной установки. Схема лабораторной установки приведена на рис. 3. В качестве источника вынуждающей гармонической ЭДС используется звуковой генератор ЗГ. При помощи ключа П1 колебательный контур подключается к генератору колебаний. Переключатель П2 позволяет включить в цепь контура конденсатор с известной емкостью С0, или с неизвестной емкостью Сx. При помощи переключа-

13

мА

Рис. 3

теля П3 можно изменить активное сопротивление контура, подключая сопротивления R1 или R2. Сила тока в контуре измеряется при помощи миллиамперметра. Значения параметров колебательного контура указаны на лабораторном макете.

Порядок выполнения работы. Ключ П1 установить в положение

“Выкл.” Включить звуковой генератор и дать ему прогреться 10 мин. В цепь колебательного контура включить конденсатор известной емкости С0 и сопротивление R1. При помощи ключа П1 замкнуть цепь контура и убедиться, что на генераторе установлены рекомендуемые диапазон частот и выходное напряжение.

Провести измерения силы тока в контуре, последовательно изменяя частоту подаваемой ЭДС. Убедившись в наличии резонанса, следует с особой тщательностью провести измерения силы тока вблизи резонансной частоты (эти измерения нужно проводить через меньшие интервалы частот). Заменив в контуре сопротивление R1 на R2, повторить измерения.

Далее, включив в контур конденсатор C0, провести аналогичные измерения с активными сопротивлениями в контуре R1 и R2.

По окончании измерений выключить звуковой генератор и разомкнуть ключ П1.

Вычисление результатов и оформление отчета. По результатам из-

мерений при включенном в контур конденсаторе C0 постройте на одном графике две резонансные кривые, соответствующие включенным в контур сопротивлениям R1 и R2. По оси абсцисс следует отложить циклическую частоту ω , связанную с частотой колебаний f соотношением ω = 2π f. По оси ординат следует откладывать действующее значение силы тока I, измеряемое при помощи миллиамперметра.

14

Далее проводят анализ графиков (резонансных кривых). В итоге этого анализа определяются резонансные частоты и ширина кривых на уровне половинной мощности ω 1 и ω 2 (рис. 2). Следует также вычислить добротности контуров Q1 и Q2, сопротивления R1 и R2, волновые сопротивления ρ 1 и ρ 2. Теоретические значения резонансных частот можно получить по формуле (15), исходя из соответствующих значений L и С. Однако отметим, что данные, приведенные на лабораторном макете, не учитывают емкость и индуктивность включенного в цепь миллиамперметра. Поэтому экспериментальные и расчетные значения резонансных частот, могут ощутимо расходиться.

По результатам измерений, выполненных с включенным в контур конденсатором неизвестной емкости Cx и сопротивлениями в контуре R1 и R2, постройте две резонансные кривые на одном графике. По экспериментально найденным значениям резонансных частот и известной индуктивности контура L вычислите значение Cx. По графикам определите ширину резонансных кривых на уровне половинных мощностей, вычислите добротности Q3 и Q4, волновые сопротивления ρ 3 и ρ 4, активные сопротивления R1 и R2. Сравните результаты с ранее найденными значениями. Оцените систематические погрешности вычисленных величин.

Дополнение: о добротности колебательного контура. 1. При выводе формулы для добротности (22) опираемся на формулу ширины резонансной кривой (19). Наметим вывод этого факта. Максимум тока достигается при минимальном значении импеданса Z0min = R. Соотношение (18)

(с учетом (13) и (16)) означает, что (Z0)2 / (Z0min )2 = 2 для ω = ω 1, ω 2. Отсюда, по формуле (11) получаем

где учитываем, что (LC)–1 = ω 02 (ниже принято традиционное обозначение ω 0 = ω р). Обозначая γ = R/L, запишем (23)

15

Сокращая обе части этого соотношения на (ω 2 + ω 1) и вспоминая, что g = R/L, получаем

т. е. приходим к формуле (19).

2. Добротность полезно связать с величиной, называемой временем релаксации. Дифференциальное уравнение затухающих колебаний имеет вид

L dIdt + IR + C1 q = 0

(уравнение (2 ), где ε = 0 ), или

q'' + 2β q' + ω 02 q = 0 (2β = R/L, ω 02 = 1/LC ).

Для таких колебательных процессов известно, что частота колебаний

ω= (ω 02 – β 2) 1/2,

аамплитуда убывает по закону

Параметр τ – время релаксации. По определению, τ – это такой промежуток времени, за который амплитуда колебаний убывает в e раз.

Добротность колебательной системы пропорциональна числу колебаний N, совершаемых за время релаксации

Переходя к параметрам β = 1 /τ , ω = 2π /T и считая β << ω 0, можно записать формулу (28)

Определение (29) приводит к той же формуле (22) (и при этом не опирается на свойства резонансных кривых).

16

КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯ

1.Приведите схему включения колебательного контура.

2.Какой вид имеет уравнение затухающих колебаний в комплексной форме? Как выражается его решение?

3.Что называют импедансом колебательного контура?

4.В чем состоит явление резонанса? Что такое резонансная частота?

5.Какую величину называют добротностью колебательного контура, по каким формулам она вычисляется?

6.Дайте определение волнового сопротивления колебательного кон-

тура.

17

Лабораторная работа № 3

ОПРЕДЕЛЕНИЕГОРИЗОНТАЛЬНОЙСОСТАВЛЯЮЩЕЙ НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ ЗЕМЛИ, ЭЛЕКТРИЧЕСКОЙ ПОСТОЯННОЙ СИСТЕМЫ СИ И СКОРОСТИ ЭЛЕКТРОМАГНИТНЫХ ВОЛН В ВАКУУМЕ

Цель работы. Определение горизонтальной составляющей напряженности магнитного поля Земли, электрической постоянной СИ и скорости электромагнитных волн в вакууме.

Методические указания. Направление линий напряженности магнитного поля можно определить с помощью магнитного диполя. Магнитный диполь – это виток с током. Предположим, что виток может поворачиваться вокруг закрепленной вертикальной оси. В магнитном поле виток установится так, что нормаль к нему укажет направление вектора напряженности H. Если отклонить виток в сторону от направления поля, то возникнет момент сил, стремящийся вернуть виток в исходное положение.

Аналогом магнитного диполя является магнитная стрелка. Размещенная на вертикальной оси стрелка застывает в положении устойчивого равновесия, показывая направление магнитного поля.

Информацию о направлении поля H можно использовать и для нахождения величины напряженности поля, вернее, величины одной из компонент этого поля по другой известной его компоненте. Если горизонтально расположенную магнитную стрелку поместить в центре круговой катушки с током, то на стрелку будет действовать магнитное поле Земли и магнитное поле тока. Горизонтальное магнитное поле H в этом случае

где H1 = Hг – горизонтальная составляющая напряженности магнитного поля Земли; H2 – напряженность магнитного поля тока.

Пусть плоскость катушки вертикальна и совпадает с плоскостью магнитного меридиана, тогда векторы H1 и H2 будут в центре катушки

18

взаимно перпендикулярны, а тангенс угла, на который отклонится стрелка при включении тока, будет равен (рис. 1)

В центре круговой катушки напряженность H2 магнитного поля определяется по формуле

Таким образом, измерив силу тока в круговом проводнике, определив угол α , на который отклоняется магнитная стрелка, а также, зная радиус витка R и число витков N, можно определить горизонтальную составляющую напряженности магнитного поля Земли

Известно, что электроемкость конденсатора С пропорциональна диэлектрической проницаемости ε вещества, заполняющего пространство между обкладками. Поэтому можно записать

где ε 0 – электрическая постоянная системы СИ; ε – диэлектрическая проницаемость (для воздуха ε ≈ 1); K – коэффициент пропорциональности, величина которoго зависит от формы, размеров обкладок конденсатора и расстояния между ними.

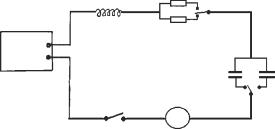
Емкость конденсатора можно измерить различными способами и, в частности, пользуясь тангенс-гальванометром. Для этого собирают электрическую схему, включающую тангенс-гальванометр Г, источник питания Б, конденсатор С, электромагнитный переключатель П (рис. 2). В положении переключателя а конденсатор заряжается до напряжения U, при этом на пластинах конденсатора скапливается заряд

В положении переключателя П, обозначенном на рис. 2 буквой b, конденсатор разряжается через тангенс-гальванометр. Если ν – число переключений в секунду, то сила тока, протекающего через тангенсгальванометр,

19

Расположив ветки обмотки тангенс-гальванометра параллельно плоскости магнитного меридиана и измерив угол поворота магнитной стрелки α 1, из формулы (4) определим силу тока

Значение горизонтальной составляющей напряженности магнитного поля Земли Hг определено в предыдущем опыте. На основании формул

(8) и (9) определяется электрическая постоянная системы СИ (при ε = I).

(численное значение коэффициента K указано на макете установки).

где µ0 = 4π ·10–7 Гн/м – магнитная постоянная системы СИ.

Описание лабораторной установки. Электрическая схема установки для определения горизонтальной составляющей напряженности магнитного поля Земли приведена на рис. 3. Необходимая величина силы тока через тангенс-гальванометр устанавливается с помощью реостата R и контролируется миллиамперметром мA. Тангенс-гальванометр состоит из деревянного круга, на внешней стороне которого намотана катушка, содержащая N витков. В центре круга горизонтально расположена магнитная стрелка, которая может вращаться вокруг вертикальной оси.

Для определения электрической постоянной системы СИ собирают схему, представленную на рис. 2. В качестве переключателя используется реле, обмотка которого включается в сеть. При этом число переключений в секунду равно частоте переменного напряжения в сети

(ν = 50 Гц).

Порядок выполнения работы. Устанавливают тангенс-гальванометр таким образом, чтобы магнитная стрелка располагалась в плоскости круга. Затем собирают схему, приведенную на рис. 3. Перед включением схемы необходимо ввести полное сопротивление реостата R. После проверки схемы преподавателем замыкают ключ П и при помощи реос-

20