Nefedov

Из квантовой теории атома известно, что дискретные (отдельные) атомы имеют дискретный энергетический спектр

– электроны в атоме могут занимать только вполне определенные энергетические уровни. В невозбужденном (нормальном) состоянии атома часть разрешенных энергетических уровней заполнена электронами, а на других разрешенных энергетических уровнях электроны могут находиться только тогда, когда атом подвергнут внешнему энергетическому воздействию (тепловому, электромагнитному и т. д.), т. е. когда атом находится в возбужденном состоянии. Атом, как и любая другая физическая система, стремится к своему устойчивому состоянию, т. е. к состоянию с минимальной энергией. При переходе из возбужденного в устойчивое состояние атом излучает избыток энергии в момент перехода электронов с возбужденных уровней на устойчивые разрешенные уровни, на которых энергия минимальна.

При сближении атомов происходит перекрытие их электронных оболочек, что существенно изменяет характер движения валентных электронов. Благодаря перекрытию электронных оболочек электроны без изменения энергии посредством обмена могут переходить от одного атома к другому. Обменное взаимодействие имеет чисто квантовую природу и является следствием неразличимости электронов. В этом случае нельзя говорить о принадлежности валентных электронов к конкретному атому, так как каждый валентный электрон принадлежит всем атомам кристаллической решетки одновременно.

Вследствие обменного взаимодействия дискретные энергетические уровни изолированного атома расщепляются в энергетические зоны. Разрешенные энергетические зоны разделяются запрещенными энергетическими интервалами. Расщеплению в зоны подвержены не только стационарные (нормальные) энергетические уровни, но и возбужденные энергетические уровни. Ширина разрешенных энергетических зон и запрещенных энергетических интервалов определяются природой атомов, образующих твердое тело и симметрией кристаллической решетки.

Каждая энергетическая зона состоит из множества энергетических уровней. Очевидно, что количество энергетических уровней определяется числом атомов, составляющих твердое тело. В кристалле объемом 1 см3 содержится 1022 – 1023 атомов, а экспериментально установлено, что энергетическая протяжен-

61

ность зоны валентных электронов не превышает единиц элект- рон-вольт. Поэтому энергетический зазор между отдельными уровнями в пределах энергетической зоны чрезвычайно мал и составляет 10–22 – 10–23 эВ, что позволяет сделать вывод о квазинепрерывном спектре электронов в пределах энергетической зоны. Это означает, что достаточно ничтожно малого энергетического воздействия, чтобы вызвать переход электронов с одного уровня на другой, если там имеются свободные энергетические состояния.

Согласно принципам квантовой механики, на каждом энергетическом уровне может находиться не более двух электронов, имеющих различные направления спинового магнитного момента (возможны только два спиновых состояния +1/2 и –1/2). Поэтому число электронных состояний в зоне оказывается конечным и равным числу соответствующих атомных состояний. Конечным будет и число электронов, заполняющих данную энергетическую зону.

Из сказанного следует, что разрешенные энергетические зоны могут быть полностью заполненными электронами, частично заполненными и свободными от электронов. Так как внутренние оболочки атома полностью заполнены электронами, то и соответствующие им энергетические зоны также будут заполнены электронами. Самую верхнюю из заполненных электронами энергетических зон образуют валентные электроны (электроны внешней оболочки изолированного атома), поэтому данную зону принято называть валентной.

Ближайшую к валентной зоне свободную (незаполненную электронами) зону называют зоной проводимости.

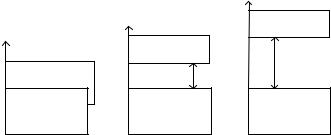
Взаимное расположение валентной зоны и зоны проводимости определяет большинство процессов, происходящих в твердом теле. Характер энергетического спектра у металлических проводников, полупроводников и диэлектриков существенно различается (рис. 1).

У металлических проводников валентная зона заполнена электронами не полностью и валентная зона, и зона проводимости частично перекрываются (рис. 1, а). В полупроводниках и диэлектриках зона проводимости и валентная зона разделены некоторым энергетическим зазором, называемым запрещенной зоной (∆Wg). Формально к полупроводникам относят вещества, у которых величина запрещенной зоны менее 3 эВ (рис. 1, б), а к

62

Рис. 1 Энергетические зоны: а – проводников; б – полупроводников; в – диэлектриков

диэлектрикам – с шириной запрещенной зоны более 3 эВ (может достигать 10 эВ) [рис. 1, в].

Внешнее электрическое поле оказывает влияние на электроны в кристаллической решетке либо замедляя, либо ускоряя их движение. Подобное замедление и ускорение связано с изменением энергии электронов, что в свою очередь сопровождается их переходом на другие энергетические уровни (состояния). Очевидно, что такие переходы электронов возможны лишь в том случае, если в энергетической зоне есть свободные уровни энергии.

Вметаллах валентная зона либо не полностью укомплектована электронами, либо перекрывается свободной от электронов зоной проводимости. Поэтому даже слабое электрическое поле способно сообщить электронам достаточный импульс для их перехода в возбужденное состояние, т. е. вызвать их переход на ближайшие свободные энергетические уровни. При этом энергия внешнего электрического поля поглощается веществом.

Вполупроводниках и диэлектриках при абсолютном нуле температуры (0° К) электроны находятся в валентной зоне, заполняя все ее разрешенные энергетические уровни. Зона проводимости является полностью свободной от электронов. Электроны полностью заполненной валентной зоны не могут перемещаться под действием слабого электрического поля, так как для их перемещения отсутствуют разрешенные свободные энергетические уровни в валентной зоне. Для появления электропроводности необходимо часть электронов перевести в свободную зону проводимости, для этого им необходимо сообщить

63

энергию, величина которой больше значения ширины запрещенной зоны.

Данная энергия может быть сообщена, например, нагревом тела. Средняя кинетическая энергия тепловых колебаний атомов в кристаллической решетке (трехмерном пространстве) равна 3/2kT, где k – постоянная Больцмана; T – абсолютная температура, и для комнатной температуры приблизительно равна

0,04 эВ.

Как отмечалось ранее, физическое тело всегда стремится вернутьсякустойчивомусостоянию,характеризуемомуминимумом энергии. Поэтому электроны из возбужденного состояния будут стремиться вернуться в равновесное состояние, при этом будет происходить излучение энергии. Так, при переходе электрона с нижнего уровня зоны проводимости («дно» зоны проводимости) на верхний уровень валентной зоны («потолок» валентной зоны) происходит выделение энергии

где h = 6,67 10–34, Дж с – постоянная Планка; ν – частота излучения, 1/c; c – скорость света, м/с; λ – длина волны.

Очевидно, чтобы из устойчивого состояния перевести электрон в возбужденное состояние последний должен получить дополнительную энергию, достаточную для такого перехода. В рассматриваемой работе источником дополнительной энергии является энергия электромагнитных волн оптического диапазона, величина которой определяется по формуле (1) и может быть достаточно просто измерена. Энергетическим условием перехода электронов из валентной зоны в зону проводимости является соотношение

∆W ≥ ∆Wg.

2.Порядок выполнения лабораторной работы

1.Объект исследования: кристаллы ZnSe и GaP.

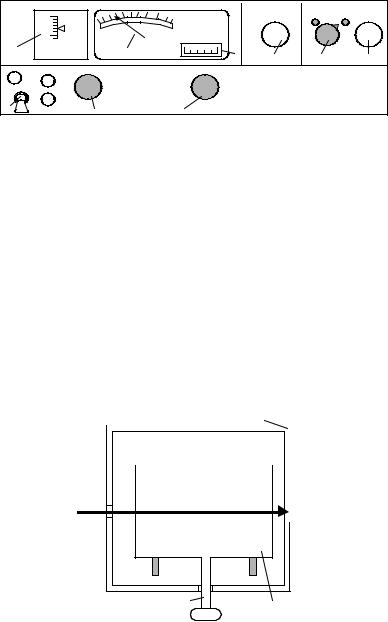
2.Схема лабораторной установки. Лабораторная установка представляет собой спектрофотометр СФ-26 с установленными

внем пластинами исследуемых кристаллов (рис. 2). Принцип работы прибора следующий. Свет от источника (лампы накаливания) превращается в параллельный пучок и подается на

64

Рис 2. Передняя панель СФ-26 (органы управления, не используемые в работе, не показаны)

диспергирующую призму, где разлагается в спектр. Требуемый участок спектра вырезается с помощью щели. Ширина щели может изменяться в пределах от 0,01 до 20 мм (ручка 1) и контролируется по шкале ЩЕЛЬ (2). Поток лучей вырезанного участка спектра попадает на фотоприемник, выходное напряжение которого регистрируется стрелочным прибором (3). Относительная интенсивность Т светового потока (при выбранной ширине щели) отсчитывается по верхней шкале стрелочного прибора. Длина волны спектральной составляющей изменяется путем поворота диспергирующей призмы (ручка 4) и контролируется по шкале ДЛИНА ВОЛНЫ (5). Если на пути светового потока поместить исследуемый образец, то стрелочный прибор зарегистрирует только ту часть потока, которая пройдет через образец.

Светонепроницаемый отсек

Рис. 3. Схема размещения образцов

65

В работе исследуется спектр оптической прозрачности кристаллов ZnSe и GaP в диапазоне волн от 640 до 400 нм. Исследуемые образцы размещаются в светонепроницаемом отсеке спектрофотометра (кювете) между оптической системой и фотоприемником (рис. 3), закрепляются на специальной каретке и могут перемещаться в направлении перпендикулярном световому потоку с помощью выдвижного штока, на который насажена ручка (6). При полностью вдвинутом штоке на пути светового потока оказывается образец ZnSe, при полностью выведенном – образец GaP. Среднее положение, отмеченное красной меткой на выдвижном штоке, соответствует прямому попаданию светового потока на вход фотоприемника.

Порядок выполнения экспериментальной части работы

Порядок подготовки и включения спектрофотометра. Перед включением спектрофотометра в сеть в присутствии преподавателя (лаборанта) ознакомьтесь с размещением исследуемых образцов. Проверьте положение органов управления спектрофотометра: переключатель ЗАКР-ОТКР (7) должен находиться в положении ЗАКР; переключатель К-Ф на верхней панели СФ-26 должен находиться в положении Ф (фотометрия); ручка НУЛЬ (8) должна быть была повернута до предела по часовой стрелке.

Включите спектрометр:

–установите ширину щели – 0,3 мм (ручка 1, шкала ЩЕЛЬ 2);

–включите вилку шнура питания спектрофотометра в розетку, а тумблер (9) переключите в положение СЕТЬ, при этом должны загореться две лампочки: лампочка СЕТЬ и красная лампочка Н;

–дайте спектрофотометру прогреться в течение 15 мин.;

–ручкой НУЛЬ (8), установите стрелку прибора (3) на нулевую отметку верхней шкалы.

1. Измерение спектральной характеристики системы «источник света – фотоприемник»:

–поставьте выдвижной шток с помощью ручки (6) в среднее положение (выдвиньте шток до появления красной метки);

–установите длину волны 640 нм (ручка 4);

–переключатель ЗАКР-ОТКР (7) переведите в положение ОТКР;

–медленно уменьшая длину волны (ручка 4), добейтесь максимального отклонения стрелки, и затем, изменяя ширину щели

66

(ручка 1), установите стрелку прибора на отметку 100% (Т0 =

Т0(max) = 100 %). В дальнейшем ширину щели не менять! После этого снова установите длину волны 640 нм;

– изменяя длину волны через 20 нм, определите относительную интенсивность Т0 спектральных составляющих в диапазоне длин волн от 640 до 400 нм, и результаты запишите в табл. 1.

Таблица 1

Экспериментальные и расчетные характеристики

2. Измерение оптической прозрачности образцов ZnSe и GaP. Образец ZnSe:

–установите длину волны 640 нм;

–полностью вдвиньте выдвижной шток (при этом на пути светового потока окажется образец ZnSe);

–изменяя длину волны через 20 нм, определите относитель-

ную интенсивность спектральных составляющих Т1 в диапазоне длин волн от 640 до 400 нм и результаты запишите в табл. 1;

при некоторой длине волны (граница световой прозрачности λгр) интенсивность спектральной составляющей, прошедшей че-

рез образец, становится равной нулю Т1 = 0 и при дальнейшем уменьшении длины волны не изменяется; медленно изменяя λ вблизи Т1 = 0, определите точное значение λ1гр и запишите его

втабл. 2.

Таблица 2

Значения граничных длин волн

Образец GaP:

– установите длину волны 640 нм;

67

– полностью выдвиньте шток (при этом на пути светового потока окажется образец GaP);

– по аналогии с образцом ZnSe измерьте оптическую прозрачность Т2 = f(λ ) и граничную длину волны λ2гр; результаты запишите в табл. 1 и 2.

Внимание! После окончания измерений необходимо:

– переключатель (7) перевести в положение ЗАКР.;

– выключить тумблер СЕТЬ (9);

– вынуть вилку шнура питания спектрофотометра из сетевой розетки.

3. Обработка результатов измерений:

– рассчитайте нормирующие коэффициенты K = T0(max)/T0 и нормированные интенсивности спектральных составляющих T1′ = T1K,% и T2′= T2K,% для всех длин волн, для которых проведены измерения; результаты расчетов запишите в табл. 1.

– постройте на одном графике зависимости Т′1 = f1(λ) и Т′2 = = f2(λ) образцов ZnSe и GaP; там же нанесите уровень Т0 =

= Т0 (max) = 100%;

– рассчитайте ширину запрещенной зоны ∆W в электронвольтах (1эВ = 1,6 10–19 Дж) для образцов ZnSe и GaP по фор-

муле

∆Wg = λhc ,

гр

где h = 6,67 10–34, Дж·с – постоянная Планка; с = 3 108, м/с – скорость света; λгр – граничная длина волны, м.

3. Содержание отчета

1.Цель работы.

2.Перечень оборудование.

3.Результаты измерений и расчетов.

4.Выводы.

Контрольные вопросы

1.Почему ширина запрещенной зоны характеризует электрические свойства твердых тел?

2.Какое физическое явление лежит в основе изучаемого метода определения ширины запрещенной зоны?

3.В каких пределах должна находится величина ширины запрещенной зоны, чтобы ее можно было измерить на данном спектрофотометре?

68

Рекомендуемая литература

1.Жеребцов И. П. Основы электроники. 5-е изд., перераб. и доп. Л.: Энергоатомиздат, 1989. 352 с.

2.Епифанцев Г. Н., Шена В. П. Твердотельная электроника: учебник для студентов вузов. М.: Высш. шк., 1986. 304 с.

69

70