Nefedov

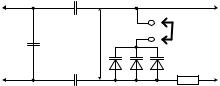
Стабильность характеристик варикапа зависит от температурных коэффициентов емкости и добротности варикапа (TKE ≈ (100–200) 10–6 1/град).

Германиевые варикапы работают при температурах не выше + 60°С, арсенид-галиевые – не выше +150°С.

Изменение емкости обычно находится в пределах от (90 – 250) до (6 – 40) пФ при изменении напряжения на p-n-переходе от 0,1

до (25 – 130) В.

Благодаря малым размерам, высокой добротности (50 – 100) и стабильности, а также значительному изменению емкости при изменении напряжения варикапы нашли широкое применение в аппаратуре для настройки контуров и фильтров в качестве элементов управления генераторов и т. п.

2.Порядок выполнения работы

1.Объект исследования: варикап 2В110А.

2.Описание лабораторной установки.

В состав лабораторной установки входят:

–измеритель добротности (Q-метр) Е4-11 с образцовой катуш-

кой индуктивности, подключенной к клеммам Lx на верхней панели Q-метра (инструкция по работе с Q-метром находится на рабочем месте);

–источник питания постоянного тока Б5-45 с укрепленным на нем делителем выходного напряжения.

–лабораторный макет, включающий в себя (рис. 4): исследуемый варикап 2В110А (для повышения точности измерения исследуется не один, а три параллельно включенных варикапа), перемычка П, позволяющая отключать варикапы, резистор и

конденсаторы. Лабораторный макет подключается к клеммам Сх на верхней панели Q-метра.

Рис. 4. Схема лабораторной установки

41

Добавочный конденсатор Сдоб = 51 пФ служит для снижения резонансной частоты измерительного колебательного контура, а конденсатора по 5600 пФ являются разделительными.

Если пренебречь влиянием разделительных конденсаторов, то при отключенных варикапах резонансная емкость колеба-

тельного контура Q-метра будет равна Ск = С1 + Сдоб, где С1 – емкость измерительного конденсатора Q-метра при резонансе, а

при включенных варикапах та же самая резонансная емкость Ск = С2 + Сдоб + 3Св, где С2 = емкость измерительного конденсатора при резонансе; Св – емкость варикапа.

Порядок выполнения экспериментальной части работы

Внимание! Проверьте, чтобы до начала измерений было следующее:

– тумблеры питания приборов Е4-11 и Б5-45 были включены;

– декадный переключатель напряжений прибора Б5-45 стоял в положении 5,0 В, а декадный переключатель тока – в положении 100 мА;

– перемычка П подключена к лабораторному макету. Задание 1. Определите добротность Q1 и резонансную емкость

Ск измерительного колебательного контура с отключенными варикапами. Для этого:

– вынуть перемычку П из лабораторного макета и включить Q-метр;

– установите частоту Q-метра f = 38 МГц, пределы измерении Q = 300 и дать прогреться прибору в течение 20 мин;

– пользуясь инструкцией по работе с Q-метром, измерьте добротность Q1 контура и емкость С1 измерительного конденсатора. Результаты занесите в табл. 1 (Ск = С1 + Сдоб, где Сдоб = 51 пФ).

Задание 2. Определите емкость Св и добротность Qв варикапа при управляющих напряжениях U0 = 4,0; 6,0; 8,0; 12; 16; 24 и

40В:

–убедитесь, что на блоке питания Б5-45 установлен ток I0 = 100 мА, напряжение U = 5,0 В, и включите блок. В связи с

42

тем, что на выходе Б5-45 включен делитель напряжения 1:1,25, управляющее напряжение на варикапе окажется равным U0 =

=U /1,25 = 5, 0 /1,25 = 4,0 В;

–включите варикап (фактически три соединенных параллельно варикапа 2В110А), для этого установить перемычку П на лабораторном макете (рис. 1);

–пользуясь инструкцией по работе с Q-метром, измерьте ем-

кость С2 измерительного конденсатора и добротность Q2 контура при управляющем напряжении на варикапе U0 = 4,0 В; повторите измерения С2 и Q2 для управляющих напряжениях U0 = 6,0; 8,0; 12; 16; 24 и 40 В. Результаты занесите в табл. 2, где U – напряжение источника Б5-45; Uo– управляющее напряжение на варикапе.

Таблица 2

гдеС1 иQ1–емкостьизмерительногоконденсатораидобротность колебательного контура Q-метра при отключенных варикапах (см. задание 1); С2 и Q2 – емкость измерительного конденсатора и добротность колебательного контура с включенными вари-

43

капами; Ск – резонансная емкость колебательного контура (см. задание 2).

Задание 3. Выполните расчеты, предусмотренные табл. 1 и 2. На одном графике нанесите уровень Q1 ( горизонтальную прямую) и постройте кривые зависимости Q2, Св и Qв от управляю-

щего напряжения U0 на варикапе.

3. Содержание отчета

1.Цель работы.

2.Перечень применяемых приборов.

3.Электрическая схема лабораторного макета.

4.Результаты измерений, расчетов и графики.

5.Выводы.

Контрольные вопросы

1.Принцип работы варикапа.

2.Параметры варикапа.

3.Объясните зависимость емкости и добротности варикапа от управляющего напряжения.

Рекомендуемая литература

1.Батушев В. А. Электронные приборы. М.: Высш. шк., 1980. 383 с.

2.Жеребцов И. П. Основы электроники. Л, 1985.

3.Петров К. С. Радиоматериалы, радиокомпоненты и электроника: учебное пособие. СПб.: Питер, 2003. 512 с.

Лабораторная работа № 6

ИЗМЕРЕНИЕ УПРУГИХ И ПЬЕЗОЭЛЕКТРИЧЕСКИХ МОДУЛЕЙ ПЬЕЗОЭЛЕКТРИЧЕСКИХ КРИСТАЛЛОВ МЕТОДОМ РЕЗОНАНСА И АНТИРЕЗОНАНСА

Цель работы: ознакомиться с тензорным методом описания физических свойств кристаллов и резонансным методом измерения упругих и пьезоэлектрических свойств

1. Методические указания по подготовке к работе

Тензорное описание физических свойств кристаллов

Известно, что кристаллические тела являются анизотропными материалами, т. е. их свойства (электрические, механические

44

и др.) обычно неодинаковы в различных направлениях. Поэтому большинство свойств кристаллов описывается с помощью таких таблиц, в которых значение характеризует данное свойство в заданном направлении. Такие таблицы могут содержать различное число параметров и называются тензорами. При этом считают, что векторы и скаляры являются частными случаями тензоров, так как вектор можно задать в виде таблицы, состоящей из трех проекций вектора на оси координат, а скаляр задается таблицей, состоящей из одного коэффициента. Число коэффициентов, входящих в состав тензора, можно всегда представить в виде целой степени числа 3. Показатель этой степени носит название ранга тензора. Так, скаляр есть тензор нулевого ранга (3° = 1), а вектор – тензор первого ранга (31 = 3).

Такие свойства кристаллов, как электропроводность, диэлектрические свойства, магнитные свойства в общем случае можно описать лишь с помощью тензора второго ранга, содержащего 9 коэффициентов (32 = 9).

Рассмотрим, например, диэлектрические свойства кристаллов, характеризуемые диэлектрической проницаемостью ε. Пусть Е – вектор напряженности электрического поля, а D – вектор электростатической индукции. В изотропном теле вектор D параллелен вектору E, поэтому

Для анизотропной среды соотношения между векторами D и E получаются более сложными, так как указанные векторы уже не параллельны друг другу. Это означает, что в общем случае каждая компонента вектора D является комбинацией всех компонент вектора E

45

В кристаллографии для удобства записи обычно оси координат обозначают не X, Y, Z, а X1, X2, X3 соответственно. Причем при написании уравнений, описывающих анизотропию физических свойств кристаллов, принято проекции вектора A на оси координат Xi обозначать как Ai, где i = 1, 2, 3. С учетом принятых в кристаллографии обозначений, уравнение (3) можно переписать в виде

D1 = ε11E1 +ε12E2 +ε13E3,

D2 = ε21E1 +ε22E2 +ε23E3, (4)D3 = ε31E1 +ε32E2 +ε33E3.

Последнее уравнение можно переписать в сокращенном виде

3

Di = ∑εijEj, j=1

где i = 1, 2, 3.

И, наконец, для удобства входящий в выражение знак суммы, принято опускать и считать, что использование в правой части уравнений одинаковых индексов означает суммирование по этим индексам, а сам повторяющийся индекс называют немым индексом.

С учетом всех принятых обозначений систему уравнений (4) можно представить в виде

Di = εijEj,

где i, j = 1, 2, 3.

Для выяснения физического смысла коэффициентов εij допустим, что электрическое поле Е приложено только вдоль оси X1, т. е. E = E1, E2 = E3 = 0. Тогда из уравнений (4) следует, что

D1 = ε11E1, D 2 = ε21E2, D3 = ε31E3. Несмотря на то, что электрическое поле приложено только вдоль оси X1, вектор электро-

статической индукции D имеет компоненты не только вдоль оси X1, (компонента D1), но и вдоль направления других осей. Данное рассмотрение позволяет сказать, что в общем случае диэлектрическая проницаемость εij характеризует компоненту вектора электрической индукции D вдоль оси Xi, если вектор напряженности электрического поля E направлен вдоль оси Xj.

Диэлектрическая проницаемость кристаллов описывается тензором диэлектрической проницаемости 2-го ранга

46

ε11 ε12 ε13

ε21 ε22 ε23 .

ε31 ε32 ε33

Есликристаллобладаетнекоторойсимметриейкристаллической решетки, то число независимых коэффициентов в описании тензора уменьшается, причем часть коэффициентов может быть равна нулю. В частности, для изотропного тела тензор диэлектрической проницаемости принимает вид

Данный тензор содержит всего один независимый элемент. Воздействие внешней силы на физическое тело также характеризуется тензором второго ранга. Если тело находится под действием внешней силы, то говорят, что это тело находится в напряженном состоянии. Величина, определяемая как отношение величины действующей силы к единице площади поверхности тела, на которую воздействует сила, получила название механи-

ческого напряжения.

Рассмотрим находящийся внутри тела единичный куб с ребрами, параллельными осям координат. Если тело находится в напряженном состоянии, то на каждую грань этого куба будут действовать силы со стороны внешних по отношению к нему (выбранному кубу) частей тела. Силу, приложенную к каждой грани куба, можно разложить на три компоненты, параллельные осям.

оси Xi. Тогда, очевидно, σ11, σ22, σ33 – нормальные компоненты

напряжения, а остальные компоненты напряжения являются сдвиговыми (рис. 1).

47

Таким образом, действие внешних сил на твердое тело описывается тензорами напряжений. Из условия равновесия внутри твердого тела рассматриваемого нами куба вытекает, что тензор напряжения – есть симметричный тензор 2-го ранга, т. е. σij =

=σji, и тензор напряжений может быть записан

σ11 σ12 σ13

σ21 σ22 σ23 .

σ31 σ32 σ33

Реальные физические тела не являются абсолютно твердыми, поэтому действие внешних сил вызывает их деформацию (смещение некоторых выбранных точек внутри тела под воздействием приложенных сил, например, удлинение тела). Деформация связана с механическим напряжением (и деформация, и механическое напряжение определяются как воздействие на тело внешней силы). Продольные компоненты механического напряжения могут вызывать продольные деформации по соответствующим осям, сдвиговые компоненты напряжений могут вызывать деформации сдвига. Поэтому деформация кристалла в общем случае описывается симметричным тензором второго ранга (Sij) (как и механические напряжения)

S11 S12 S13

S21 S22 S23 .

S31 S32 S33

Упругие свойства кристаллических тел

Соотношение между деформациями и напряжениями определяются законом Гука. В частном случае для слабых деформаций (линейное приближение – после снятия внешней силы деформация пропадает) относительная деформация пропорциональна напряжению. Для анизотропных сред, где любая компонента напряжения может вызвать любую другую компоненту деформации (а не только такую же, как исходная компонента напряжения, так как смещения в материальной среде могут быть разными по разным направлениям), то в общем случае каждая компонента напряжения является линейной комбинацией всех компонент тензора деформации

где i, j, k, l = 1, 2, 3.

48

Повторяющиеся в правой части индексы i, j предполагают суммирование по этим индексам. Система из девяти уравнений

(5) содержит 81 коэффициент сijkl, который называют упругими модулями. Благодаря симметрии тензоров напряжения и дефор-

мации cijkl = cklij = cjikl = cijlk, что уменьшает число независимых коэффициентов до 36. Для изотропных тел число независимых

упругих модулей уменьшается до двух, один из которых обычно называют модулем Юнга, а другой – коэффициентом Пуассона. Из всего вышесказанного следует, что упругие свойства тел описываются тензором 4-го ранга (34 = 81) – тензором упругости cijkl (тензором модулей упругости).

Можно ввести тензор, обратный тензору упругости, который также будет тензором четвертого ранга. Тогда можно выразить деформации через напряжения

Sik = sijklσjl,

где Sik – тензор деформации; sijkl – тензор упругой податливости (тензор четвертого ранга обратный тензору упругости cijkl).

Поскольку число независимых упругих констант для тензо-

ров cijkl и sijkl не превышает 36, то на практике часто используется сокращенное (матричное) обозначение модулей упругости и

податливости, при котором вместо пар индексов (i, j) и (k, l), где i, j, k, l = 1,2,3, вводят индексы m, n = 1,2,3,4,5,6 в соответствии с таблицей

Например, s1213 ≡ s65, и в общем случае модули упругости и модули податливости могут быть записаны в сокращенном виде как cijkl cmn и sijkl smn.

Пьезоэлектрические свойства кристаллических тел

Некоторые типы твердых тел при действии на них внешних сил поляризуются, т. е. в них возникает собственное микроскопическое электрическое поле. При этом на поверхности тела появляются электрические заряды. Эффект поляризации твердого тела при действии на него внешней силы получил название пьезоэлектрического эффекта, а тела, в которых наблюдается этот эффект, называются пьезоэлектриками.

49

Если внешняя сила меняет свой знак, то знак поляризации также меняется. Пьезоэлектрический эффект обратим: у пьезоэлектриков, помещенных в электрическое поле, наблюдается изменение геометрических размеров, т. е. пьезоэлектрик деформируется во внешнем поле. Этот эффект получил название обратного пьезоэлектрического эффекта.

Экспериментально установлено, что величина пьезоэлектрической деформации в умеренных полях пропорциональна напряженности электрического поля

где S – деформация, т. е. относительное изменение соответствующих размеров пьезоэлектрика; E – напряженность электрического поля.

Коэффициент пропорциональности d носит название пьезоэлектрического модуля. Аналогичное уравнение можно написать и для прямого пьезоэлектрического эффекта.

Из уравнения (6) следует, что пьезоэлектрические свойства должны описываться тензором третьего ранга, так как коэффициент d связывает между собой тензор первого ранга (вектор) напряженности электрического поля Е и тензор механических деформаций Sij, являющийся тензором второго ранга. С учетом тензорного характера входящих в уравнение (6) величин, последнее можно представить в следующем виде:

где n = 1,2,3,4,5,6; m = 1,2,3.

Благодаря введению матричных обозначений упругие тензоры cmn и модули податливости smn кристалла можно представить квадратной матрицей размера (6х6), а пьезоэлектрические модули dnk представляются матрицей размера (6х3). Например, запись упругих и пьезоэлектрических модулей для кристалла кварца α – SiO2 имеет следующий вид:

50