
Nefedov
.pdf
Критерием «слабости» магнитного поля является соблюдение требования
By <<2π, |
(8) |
где y – подвижность носителей.
Это ограничение связано с тем, что в «сильных» магнитных полях происходит не только отклонение носителя электрического заряда, а также и закручивание его траектории вокруг линий магнитного поля. Умножив постоянную Холла на удельную электропроводность материала σ0 = |q| yn, получим
y = RХσ0. |
(9) |
Эффекту Холла обычно сопутствует ряд эффектов, которые могут внести значительные погрешности при измерении холловскойразностипотенциалов.Рассмотримнекоторыеизсопутствующих эффектов и способы устранения их влияния на точность измерений.
Погрешность, вносимая асимметрией холловских зондов
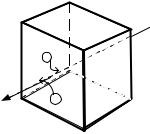
Пусть магнитное поле отсутствует. Тогда эквипотенциальные поверхности перпендикулярны линиям тока (рис. 2). Холловские зонды должны располагаться на одной эквипотенциальной
линии (расположены в симмет- |
|
|
|
UА |
|
|
|
||||
ричных точках С и D). При таком |
|
|
|
|
|
||||||
|
|
|
|
||||||||
расположении |
измерительных |
|
C |
|
|
|
|
|
C′ |
||
зондов при включении магнитно- |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
го поля будет измерено истинное |
|
|
|
|
|
|
|
|
I |
||
значение холловской разности по- |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
тенциалов. При |
асимметричном |
|
|
|
|
|
|
|
|
|
|
расположениизондов(например,в |
|
D |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
точках С’ и D) необходимо учиты- |
|
|
|
|
|
|
|
|
|
||
вать разность потенциалов между |
Рис. 2. Схема расположения |
||||||||||
этими точками UDC = UХ + UA. |
|||||||||||
|
холловских зондов |
||||||||||
Так как знак |
UА не зависит |
|
|||||||||
|
|
|
|
|
|
|
|
|
|||
от направления магнитного поля, то разность потенциалов UА можно исключить, выполняя два последовательных измерения с использованием противоположных по направлению магнитных полей. Результаты этих измерений записываются в виде
UDC' |
|
+H = UХ + UA, |
(10) |
|
|||
|
|
31
UDC' |
|
–H = −UХ +UA. |
(11) |
||||||
|
|||||||||
|
|
||||||||
Из выражений (10) и (11) получим |
|
||||||||
UХ = |
UDC' |
|
+H −UDC' |
|
−H |
. |
(12) |
||
|
|
||||||||
|
|
||||||||
|
|
|
|
|
|||||
2 |
|
|
|
|
|||||
Погрешность, вносимая продольным градиентом температуры
Термомагнитные эффекты возникают при воздействии магнитного поля на проводник, в котором имеется градиент температуры. Пусть, например, в образце (рис. 3), существует градиент температуры вдоль образ-
|
|
|
й |
ца от верхней грани В к нижней |
|
|
|
|
Холодны |
||
|
B |
грани А (TB < TA). Тогда от грани |
|||
|
|
||||
|
|
|
|||
|
|
|
|
А к грани В возникают направ- |
|
|
|
|
|
ленные, результирующие потоки |
|
|
|
|
й |
свободных носителей заряда. Они |
|
|
|
|
обусловлены тем, что на горячем |
||
|
е |
|
Горячи |
||
В |
|
|
конце образца средние скорости |
||
|
|
+ |
|||
|
|
|
|
хаотического теплового движения |
|
Рис. 3. Схема возникнове- |
выше, чем на холодном (явление |
||||
термодиффузии), а также тем, что |
|||||
ния эффекта Риги–Ледюка |
|||||
на горячем конце образца концент- |
|||||
рация носителей может оказаться выше, чем на холодном (диффузия). Между холодным и горячим концами образца появится разность потенциалов (термо-ЭДС). Эта разность потенциалов приводит к возникновению встречного по отношению к термодиффузионному потоку дрейфового потока носителей. Например, если образец представляет собой полупроводник n-типа, то термодиффузия и диффузия электронов приводят к появлению отрицательного заряда на верхней и положительного на нижней гранях образца (рис. 3). Тогда от верхней грани к нижней пойдет дрейфовый поток электронов. Термо-ЭДС нарастает до тех пор, пока дрейфовый поток не сравняется со встречным тепловым потоком. Эти два потока, однако, переносятся электронами с разными средними скоростями теплового хаотического движения. В тепловом потоке средняя скорость хаотического движения носителей выше, чем в дрейфовом. В поперечном магнитном поле эти потоки отклоняются к противоположным граням С и D. Изза разных средних скоростей хаотического теплового движения
32
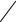
во встречных продольных потоках носителей они отклоняются магнитным полем несколько по-разному и в поперечном направлении также возникает некоторая разность потенциалов (поперечный эффект Нернста).
Эффект Нернста приводит к возникновению поперечной разности потенциалов
UH = QH∂T |
∂a |
, |
(13) |
|
|
|
где Q – коэффициент Нернста; H – напряженность поперечного магнитного поля; ∂T/∂a – продольный градиент температуры (a – длина образца, b – ширина образца).
Из уравнения (13) следует, что знак UH зависит только от направления магнитного поля. Следовательно, UH можно исключить из измеренной величины ЭДС Холла, если выполнить измерения при двух противоположных направлениях электрического тока,
U |
|
+I = −UХ +UH, |
(14) |
||||||||
|
|||||||||||
|
|
||||||||||
U |
|
−I =UХ +UH. |
(15) |
||||||||
|
|||||||||||
|
|
||||||||||
Из выражений (14) и (15) находим |
|
||||||||||
UХ = |
U |
|
+I −U |
|
−I |
. |
(16) |
||||
|
|
||||||||||
|
|
||||||||||
|
|
|
|
|
|||||||
2 |
|
|
|
|
|||||||
Кроме того, грань C, к которой отклоняется тепловой поток, окажется более горячей, чем грань D, и возникает поперечный градиент температуры, пропорциональный продольному, называемый эффектом Риги–Ледюка. Последний приводит к возникновению термопар между материалами зондов и полупроводниковой пластиной.
Знак ЭДС Риги–Ледюка UР–Л также, как знак UН, зависит только от направления магнитного поля, и следовательно, UР–Л исключается одновременно с UН путем измерений при двух противоположных направлениях электрического тока.
Таким образом, совместное влияние асимметрии холловских зондов и градиента температур можно исключить, если провести измерения при двух направлениях тока и двух направлениях магнитного поля:
33

U
UU
U
+H,+I0
−H,+I0
−H,−I0
+H,−I0
=UХ +UA +UH +UР−Л,
= −UХ +UA −UH −UР−Л,
(17)
=UХ −UA −UH −UР−Л,
= −UХ −UA +UH +UР−Л.
Решая систему уравнений (17) относительно UX, получим
UХ = |
U |
|
+H,+I0 −U |
|
−H,+I0 +U |
|
−H,−I0 −U |
|
+H,−I0 |
. |
(18) |
|
|
|
|
||||||||
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|||
4 |
|
|
|
|
|
|
|||||
2. Порядок выполнения работы
Объект исследования
Прямоугольная пластина легированного германия с размерами a = 11,5 мм; b = 7,5 мм; d = 3,5 мм, снабженная холловскими зондами и токовыми электродами и помещенная между полюсами электромагнита ЭМ.
Схема лабораторной установки
Лабораторная установка (рис. 4) включает в себя:
–блок питания электромагнита АГАТ;
–микровольтметр В2-15 для измерения величины и знака разности потенциалов U между холловскими зондами;
–блок питания образца (БПО).
А1 V1 |
|
|
|
А2 |
БПО |
|
В2 15 |
|
АГАТ |
|
|
|
|
|
ЭМ
Рис. 4. Схема лабораторной установки
34

Порядок выполнения экспериментальной части работы
1.Получите у преподавателя вариант задания: значения токов через
обмотку электромагнита IЭМ и через исследуемый образец I0.
2.Подготовьте лабораторную установку к работе:
–тумблеры питания на передних панелях БПО, В2-15 и АГАТ поставьте в положении ВЫКЛ.;
–ручку регулировки напряжения на передней панели АГАТА поверните до упора против часовой стрелки;
–регулятор тока I0 на передней панели БПО поверните до упора против часовой стрелки.
3. Проведите измерения ЭДС Холла:
–включите шнуры питания БПО, В2-15 и АГАТА в сеть электропитания;
–установите с помощью тумблеров «± H» (прибор АГАТ) и «±
I0» (прибор БПО) первое сочетание знаков Н и I0, указанное в табл. 1;
–для данного сочетания знаков Н и I0 установите указанное в табл. 1 положение переключателя пределов измерения и тумблера «полярность» (прибор В2-15);
–тумблеры питания на передних панелях БПО, В2-15 и АГАТА поставьте в положение ВКЛ., при этом стрелка прибора В2-15 отклонится вправо до предела и примерно через 15 с вернется в нулевое положение;
–с помощью ручки регулировки напряжения (АГАТ) устано-
вите (амперметр А2, вся шкала ± 5 А) значение тока IЭМ через обмотку электромагнита, указанное в задании. Дайте приборам прогреться не менее 3 мин;
–измерьте разность потенциалов между холловскими зондами для первого сочетания знаков Н и I0, для этого:
–регулятором тока (прибор БПО) установите значение тока
I0, протекающего через образец, указанное в задании (амперметр А1; вся шкала 5 мА). Отсчитайте число делений по шкале стрелочного прибора В2-15 и определите величину разности потенциалов U (в милливольтах), знак разности потенциалов определите по положению тумблера «полярность» и результаты запишите в табл. 1.
–регулятор тока I0 поверните до упора против часовой стрел-
ки;
35
–повторите измерение разности потенциалов между холлов-
скими зондами для трех следующих сочетаний знаков Н и I0
(табл. 1);
–результаты измерений занесите в табл. 1.
Таблица 1
Измеренные значения напряжения между холловскими зондами
|
Подготовка приборов к измерению |
Результаты |
||||
|
измерений |
|||||
№ |
|
|
|
|||
|
Положение |
Положение |
Число |
|
||
изме- |
Сочетание |
Знак и |
||||
переключателей |
тумблера |
делений |
||||
рения |
знаков |
величина |
||||
пределов изме- |
«полярность» |
шкалы |
||||
|
||||||
|
Н и I0 |
рения (В2-15) |
(В2-15) |
(В2-15) |
U, мВ |
|
1 |
+ Н, + I0 |
µV = 1000 х 1 |
« – » |
|
|
|
2 |
+ Н, – I0 |
Вся шкала 1,0 мВ |
« + » |
|
|
|
|
|
|
||||
3 |
– Н, + I0 |
µV = 100 х 1 |
« + » |
|
|
|
4 |
– Н, – I0 |
Вся шкала 0,1 мВ |
« – » |
|
|
|
4. Измерьте с помощью милливольтметра V1, расположенного на передней панели БПО (вся шкала прибора – 50 мВ), падение напряжения U0 на образце при значении тока I0, указанном в задании; результаты занесите в табл. 2
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
|
|
|
|
|
Параметры полупроводника |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
I0, мА |
|
|
U0, мВ |
|
|
|
R0, Ом |
|
|
|
Параметры полупроводника |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
RX, |
|
|
|
σ0, |
|
y, |
|
n, |
|
|
|
|
|
|
|
|
|
|
м3 / Кл |
1/ Ом м |
м2/ В с |
1/ м3 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Обработка результатов измерений |
|
|
||||||||||||||
1. Рассчитайте постоянную Xолла по формуле |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
RХ = UХd,м3/Кл, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
BI0 |
|
|
|
|
|
|
|
|
||
где UХ |
= |
U |
|
+H,+I0 |
−U |
|
−H,+I0 |
+U |
|
−H,−I0 |
−U |
|
+H,−I0 |
, мВ; d – толщина |
||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
образца, м; I0 – ток через образец, мА; B = µ µ0 H – магнитная индукция, Тл (µ = 1; µ0 = 4π10–7 Гн/м, H = КIЭМ – напряжен-
36
ность магнитного поля А/м, К = 49,95 103 м–1 IЭМ – ток через электромагнит, А).
2. Рассчитайте удельную электропроводность, подвижность, концентрацию и определите знак носителя заряда по формулам:
σ0 = a/ R0 b d – удельная электропроводность образца, 1/ Ом м,
где a, b и d – размеры образца, м; R0 = U0 /I0 – сопротивление об-
разца, Ом; y = | RX|σ0 – подвижность носителей, м2/ В с; n = σ0 / |q| y – концентрация носителей, 1/м3; |q| = 1,6 10–19 – величина
заряда носителя, Кл; RX = 1/ q n – соотношение для определения знака заряда.
Результаты расчетов занесите в табл. 2.
1. Содержание отчета
1.Цель работы.
2.Схема лабораторной установки.
3.Результаты измерений и расчетов.
4.Выводы.
Лабораторная работа № 5
ИССЛЕДОВАНИЕ ВАРИКАПА
Цель работы: исследовать зависимости емкости и добротности варикапа от управляющего напряжения.
1. Методические указания по подготовке к работе
Конденсатор – это электрорадиоэлемент, способный накапливать и быстро отдавать электрическую энергию. Для плоского конденсатора, состоящего из двух металлических электродов (обкладок) и диэлектрика между ними, емкость определяется по формуле
С = |
ε0εS |
, |
(1) |
|
d |
|
|
где ε0 – диэлектрическая проницаемость вакуума, ε0 = 8,86 10–12 Ф/м; ε – относительная диэлектрическая проницаемость диэлектрика; S – площадь электрода; d – толщина диэлектрика.
Конденсаторы делятся на два основных класса: конденсаторы постоянной емкости и конденсаторы переменной емкости (КПЕ). Они существенно различаются по назначению, параметрам и
37

конструкции, хотя и обладают многими общими характеристиками. КПЕ используются в РЭА для настройки колебательных контуров, изменения емкостной связи между отдельными участками электрической цепи, балансировки емкостных мостов, плавного изменения емкости по заданному закону в измерительной технике.
Как видно из выражения (1), емкость можно изменить путем изменения одного или одновременно нескольких параметров: площади перекрытия пластин S, расстояния между ними d, диэлектрической проницаемости материала диэлектрика ε. Изменение емкости конденсатора можно получить двумя способами управления – механическим (изменяя S и d) и электрически (изменяя d и ε). Конденсаторы с изменением ε называются варикондами, а с электрическим управлением d (в полупроводниковых диодах) – варикапами.
Варикап – это полупроводниковый конденсатор, емкость которого зависит от приложенного к его обкладкам напряжения. Диэлектриком конденсатора является обедненный носителями заряда слой p-n-перехода, а обкладками – прилегающие к нему проводящие объемы кристалла полупроводника.
Толщина обедненного основными носителями p-n-перехода определяется формулой
d = |
2εε0 |
(Na + Nd)(Uk ±U) |
, |
(2) |
|
qNaNd |
|||
|
|
|
|
где Na, Nd – концентрация акцепторной и донорной примесей; Uk – контактная разность потенциалов; U – внешнее напряжение, приложенное к p-n-переходу («+ » – обратное включение, «– » – прямое); q – заряд носителя.
Таким образом, толщина обедненного основными носителями слоя пропорциональна (Uk ± U)1/2 и при обратном включении увеличивается с увеличением U. Рассматривая обедненный слой как диэлектрик, заключенный между слоями полупроводников с достаточно высокой проводимостью и играющих роль обкладок, получим конденсатор, управляемый электрическим полем. При этом с изменением U изменяется расстояние между обкладками d.
В варикапе одна область полупроводника обычно легирована больше другой (например, Na >> Nd). Тогда формула (2) упроща-
38
ется. Это означает, что обедненный слой целиком лежит в слабо- |
||||||||
легированном полупроводнике (d ≈ dn) |
|
|
|
|
||||
d = |
2εε0(Uk |
±U) |
=dn. |
|
(3) |
|||
|
qNd |
|
|
|||||
|
|
|
|
|
|
|
||
В то время как в сильнолегированном полупроводнике обед- |
||||||||
ненная область очень мала, dp≈ 0. Подставив выражение (3) в |
||||||||
формулу (1), получим формулу для барьерной емкости варика- |
||||||||
па: |
|
|
|
|
|
|
|
|
Cб = S |
ε0εqNd |
. |
|
(4) |
||||
|
|
2(Uk ±U) |
|
|
|
|||
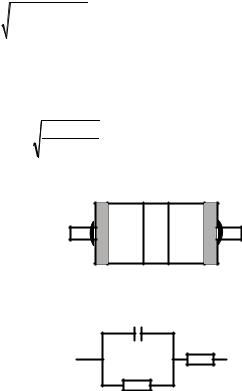
На рис. 1 приведена структура варикапа на основе p-n-пере- |
||||||||
хода. База диода состоит из низ- |
|
|
|
|
|
|||
коомной (n+) и высокоомной (n) |
|
|
|
|
|
|||
областей (знак « + » указывает |
|
|
p+ |
n |
n+ |
|||
на повышенную концентрации |
|
|
||||||
|
|
|
|
|
||||
примесей). Низкоомная часть |
|
|
|
|
|
|||
базы играет роль обкладки, а вы- |
Рис. 1. Структура варикапа |
|||||||
сокоомная часть непосредствен- |
||||||||
|
|
|
|
|
||||
но примыкает к низкоомной об- |
|
|
|
|
|
|||
ласти (p+), являющаяся второй |
|
|
Cб |
|
|
|||
обкладкой. Поэтому p-n-переход |
|
|
|
|
rб |
|||
образуется между областями p+ и |
|
|
|
|
||||
|
|
|
|
|
||||
n, и располагается в слаболегиро- |
|
|
|
|
|
|||
ванной области n. |
|
|
|
|
|
|
|
|
Основнымипараметрамивари- |
|
|
rпер |
|
|
|||
капа являются: Cб – номинальная |
Рис. 2. Эквивалентная схе- |
|||||||
емкость варикапа, измеренная |
ма варикапа: Cб – барьерная |
|||||||
при заданном обратном напряже- |
||||||||
емкость перехода; rб – со- |
||||||||
нии; Кс – коэффициент перекры- |
||||||||
противление низкоомной |
||||||||
тия по емкости, равный отноше- |
области; rпер – активное |
|||||||
нию емкостей варикапа при двух |
сопротивление обедненного |
|||||||
заданных обратных напряжений; |
|
|
слоя |
|
||||
Qв – добротность варикапа, рав- |
|
|
|
|
|
|||
ная отношению реактивного сопротивления варикапа хв на за- |
||||||||
данной частоте к сопротивлению потерь r |
|
|
||||||
Qв = xв . |
(5) |
r |
|
39
Зависимость добротности варикапа от частоты можно найти из эквивалентной схемы варикапа (рис. 2).
Полное сопротивление схемы, изображенной на рис. 2
z =rб + |
rпер |
|
|
. |
(6) |
1+ jr |
ϖс |
|
|||
|
пер |
|
б |
|
|
Подставляя (6) в (5), находим выражение для добротности варикапа
|
|
ϖс r |
2 |
|
|
|
|
|
Qв = |
|
|
б пер |
|
|
. |
(7) |
|
r |
+r |
+r r2 |
ϖ2с |
|
||||
|
б |
|
||||||
|
б |
пер |
б |
пер |
|
|
||
На низких частотах rб<< 1/vcб (отношение rб/rпер ≈ 10–7 для реальных варикапов), поэтому добротность варикапа определя-
ется соотношением
Qв =rперϖcб. |
(8) |
На высоких частотах rпер>>1/vcб, поэтому добротность варикапа будет
Q |
в |
= |
1 |
|
. |
(9) |
ϖr с |
|
|||||
|
|
в |
|
|||
|
|
|
б |
|
||
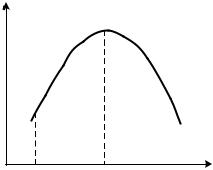
Зависимость добротности от частоты приведена на рис. 3.
Qв
Qmax
Qmin 
ϖн |
ϖopt |
ϖв ϖ |
Рис. 3. Зависимость добротности варикапа от частоты: Qmax, Qmin – максимальная и минимальная добротность; vн, vв,, vopt – низкая, высокая и оптимальная частоты
40
