
Nefedov
.pdf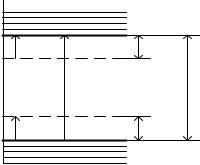
|
ЗП |
|
Wc |
∆Wd |
|
1 |
|
|
Wd |
|
|
|
ЗЗ |
∆Wg |
|
3 |
|
Wa |
∆Wa |
|
2 |
|
|
Wν |
|
|
|
ВЗ |
|
Рис. 1. Схема энергетических зон для полупроводника |
||
ные области, из которых ушли электроны в ЗП. Концентрация собственных носителей обозначается ni и pi для электронов и дырок соответственно; Wc, Wν – энергии дна зоны проводимости и потолка валентной зоны соответственно; Wd, Wa – энергии примесных донорного и акцепторного уровней соответственно; ∆Wg – ширина запрещенной зоны; ∆Wd – энергия донорного уровня относительно дна зоны проводимости; ∆Wa – энергия акцепторного уровня относительно потолка валентной зоны.
Если носители образовались в результате перехода электрона с донорного уровня (переход 1) или из ВЗ на акцепторный уровень (переход 2), то носители будут примесные (электроны в ЗП и дырки в ВЗ). Носители, образовавшиеся в результате изменения температуры полупроводника, называются равновесными, так как их концентрация находится в тепловом равновесии с кристаллической решеткой. Это означает, что при увеличении температуры концентрация будет увеличиваться, а при снижении уменьшаться. Однако появление носителей может быть вызвано воздействием ряда внешних факторов, не связанных с изменением температуры полупроводника. К ним относятся, в частности, облучение светом, введение (инжекция) носителей из контактирующего с полупроводником тела (например, металла) или соседних участков этого же полупроводника под действием электрического поля или градиента концентрации (диффузии). Образующиеся таким образом избыточные носители не находятся в тепловом равновесии с полупроводником, и поэтому называются неравновесными. Полная концентрация носителей будет равна сумме равновесных и неравновесных носителей.
21

Подвижность µ определяет скорость направленного движения (дрейфа) носителя в электрическом поле: Vдр = µ Е, где Vдр – скорость дрейфа носителя; Е – напряженность электрического поля. Численно µ равна скорости дрейфа в электрическом поле с Е = 1.
Следуетпомнить,чтонарядуспроцессомобразования(генерации) неравновесных носителей, идет процесс их рекомбинации, при котором встречающиеся электрон и дырка аннигилируют. Окончательная концентрация носителей будет определяться равенством скоростей этих двух процессов. Рекомбинации характеризуются временем жизни носителя (tn и tp) т. е. временем, в течение которого концентрация носителей уменьшается в е раз
(е = 2,718).
Для описания поведения носителей в полупроводнике, находящемся под воздействием внешних факторов, составляется уравнение баланса концентраций неравновесных носителей заряда во времени и в пространстве. Это уравнение называется уравнением непрерывности. Для одномерного случая (т. е. когда рассматривается изменение концентрации неравновесных носителей вдоль одной оси, например Х), уравнения имеют вид
для электронов:
∂n = g(x,t)− |
∆n −µnE |
∂n −Dn |
∂2n |
, |
||||
∂t |
|
τn |
∂x |
|
∂x2 |
|
||
для дырок: |
|
|
|
|
|
|
|
|
∂p |
= g(x,t)− |
∆p −µpE |
∂p |
|
+ Dp |
∂2 p |
, |
|
∂t |
∂x |
∂x2 |
||||||
|
τp |
|
|
|||||
где g(x,t) – скорость образования неравновесных носителей; ∆n,∆p – концентрация неравновесных носителей (электронов и дырок соответственно); τn, τp – время жизни носителей (электронов и дырок соответственно); µn, µp – подвижность носителей (электронов и дырок соответственно); E – напряженность элек-
трического поля; ∂∂nx,∂∂xp – градиенты концентраций носителей
(электронов и дырок соответственно); Dn, Dp – коэффициенты диффузии носителей (электронов и дырок соответственно).
Диффузия – это направленный перенос носителей в сторону уменьшения их концентрации. Плотность диффузионного пото-
22

ка Ф, равная числу носителей, проходящих через 1 м2 в 1 с, пропорциональна градиенту концентрации
Ф = −D ∂∂nx,
где D – коэффициент диффузии, зависящий от природы взаимодействующих веществ и температуры.
Для характеристики рекомбинационных процессов вводится понятие диффузионной длины носителя, которая равна
для электронов:
Ln = 
 Dnτn,
Dnτn,
для дырок:
Lp = 
 Dрτр .
Dрτр .
Диффузионной длиной носителя называется отрезок, на котором его концентрация уменьшается в е раз (2,718 раз).
Коэффициент диффузии связан с подвижностью носителей соотношением Эйнштейна
для электронов:
µп = qDkTп ,
для дырок:
µ p = qDkTp .
Общие свойства p-n-перехода
При контакте двух полупроводников с различным типом носителей на границе возникают диффузионные процессы: электроны из полупроводника п-типа перемещаются в полупроводник р-типа, а дырки из полупроводника р-типа – в полупроводник п-типа. В результате нарушается электронейтральность прилегающих к границе областей полупроводников, что приводит к возникновению контактной разности потенциалов. Эту область называют р-п-переходом. Контактная разность потенциалов создает потенциальный барьер, препятствующий дальнейшей диффузии основных носителей и способствующий дрейфу неосновных носителей. Так как потоки основных и неосновных но-
23
сителей направлены навстречу друг другу, то при некотором значении контактной разности потенциалов наступает равновесие. Электрофизические свойства образовавшегося таким образом p-n-перехода определяются следующими характеристиками:
– контактная разность потенциалов Vк;
– концентрации акцепторных примесей в р-области Na и донорных примесей в п-области Nd;
– толщина p-n-перехода δp-n;
– барьерная емкость перехода Cб/U = 0;
При приложении внешнего электрического поля к p-n-пере- ходу, последнее будет либо уменьшать величину потенциального барьера (прямое включение), либо увеличивать (обратное включение). Следовательно, при прямом включении будет увеличиваться диффузионный ток основных носителей и уменьшаться дрейфовый ток неосновных носителей, а при обратном включении – наоборот. Так как концентрация основных носителей на несколькопорядковбольше,чемнеосновных,тоувеличениетока при прямом включении p-n-перехода существенно выше, чем при обратном. Эта особенность p-n-перехода отражена в вольт-ампер- ной характеристике.
2.Порядок выполнения работы
1.В данной работе экспериментальным путем определяются
Vк, Na, Nd, а затем рассчитываются остальные характеристики p-n-перехода.
2.Объект исследования: p-n-переход германиевого диода
Д304.
3.Схемы исследования.
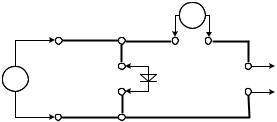
Схема измерения прямой ветви вольт-амперной характеристики (ВАХ) диода приведена на рис. 2.
Схема собирается на монтажном шасси с использованием комплекта соединительных проводов. Напряжение питания подает-
|
A |
0–300мА |
|
|
+ |
V 0–0,75В |
Д304 |
Г7 |
|
|
_ |
Рис. 2. Схема измерения прямой ветви ВАХ
24
ся от источника 0 – 3В (гнезда Г7 блока 3 лабораторного стенда). Токи и напряжения измеряются внешними стрелочными измерительными приборами. Пределы измерений приборов указаны на схеме.
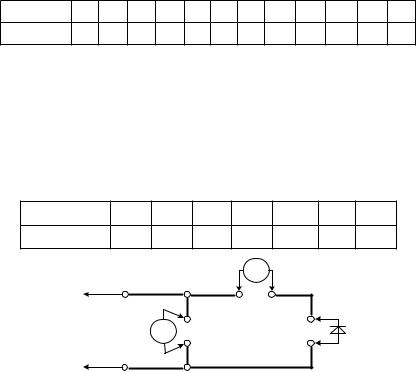
Схема измерения обратной ветви вольт-амперной характеристики диода приведена на рис. 3. Напряжение питания подается от источника 0 – 15В (гнезда Г8 блока 3 лабораторного стенда).
Порядок выполнения экспериментальной части работы
1.Соберите схему, изображенную на рис. 2.
2.После проверки схемы преподавателем измерьте Uпр прямой ветви вольт-амперной характеристики диода; значения прямого тока устанавливайте в соответствии с табл. 1.
Таблица 1
Значения прямого напряжения
Iпр, мА |
0 |
2 |
10 20 30 40 80 120 160 200 240 280 |
Uпр, В
3.Соберите схему, изображенную на рис. 3.
4.После проверки схемы преподавателем измерьте Iобр обратной ветви вольт-амперной характеристики диода. Отсчет напря-
жения Uобр начинайте с Uобр = 10 В и заканчивайте Uобр = 1 В (10, 8, …, 1); после точки Uобр = 1 В снимите напряжение, выдернув штекер «+» из гнезда Г8 (это соответствует Uобр = 0 В.
Таблица 2
Значения обратного тока
Uобр, В |
10 |
8 |
6 |
4 |
2 |
1 |
0 |
Iобр, мА |
|
|
|
|
|
|
|
|
|
|
|
A |
0–0,75 мА |
|
|
|
+ |
|
|
|
|
|
|
Г8 |
|
V |
0–15 В |
|
|
|
|
|
_ |
|
|
|
|
|
|
Рис. 3. Схема измерения обратной ветви ВАХ
25
Обработка результатов измерений
1.Постройте вольт-амперную характеристику диода (зависимость тока, протекающего через диод от напряжения на диоде). Прямую и обратную ветви стройте на одном графике, используя разные масштабы.
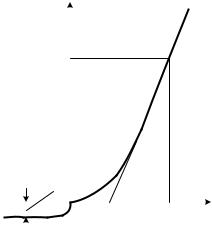
2.Определите контактную разность потенциалов Vк, графическим путем, продлив линейные участок прямой ветви вольтамперной характеристики до пересечения с осью напряжений
(рис. 4).
3.Определите концентрации акцепторной примеси в р-облас-
ти Nа, и донорной примеси в п-области Nd. Система уравнений для расчетов:
|
|
|
|
|
D |
n |
|
|
|
Dp |
|
|
|||
I |
0 |
= Sq |
|
|
|
+ |
|
|
n2 |
|
|
||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
NaLn |
|
|
i |
|
|
||||||
|
|
|
|
|
NdLp |
(1) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
Vк = |
kT |
ln |
NaNd |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
||||||
q |
|
|
|
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
ni |
|
|
|
|
|
|||
где I – обратный ток насыщения (рис. 4); q = 1,6 10–19 Кл – заряд |
|||||||||||||||
0
электрона; k = 1,38 10–23 Дж/К – постоянная Больцмана; T(K) – температура исследуемого перехода; S – площадь поперечного сечения p-n-перехода задается преподавателем: вариант 1 – S =
|
|
|
Iпр , мА |
|
|
= 0,075 10–4 м2; |
вариант |
||
|
|
|
|
|
2 – S = 0,1 10–4 м2; вариант |
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
3 – S = 0,125 10–4 м2; Dn, |
|||
|
|
|
|
|
|
Dp, Ln, Lp, ni – парамет- |
|||
|
|
|
|
|
|
ры собственного полупро- |
|||
|
|
|
|
|
|
водника (германия) при |
|||
|
|
|
|
|
|
Т = 300 К; D |
n |
= 1,01 10–2 |
|
|
|
|
|
|
|
м2/c – коэффициент диф- |
|||
|
|
|
|
|
|
фузии электронов; Dp = |
|||
|
|
|
|
|
|
0,49 10–2 м2/c – коэффици- |
|||
|
|
|
|
|
|
ент диффузии дырок; Ln = |
|||
Uобр , В |
|
I0 |
|
Uпр , В |
1,0 10–3 м – диффузионная |
||||
|
|
длинаэлектроноввр-облас- |
|||||||
|
|
|
|||||||
|
|
|
|
|
|
ти; L = 9,0 10–4 м – диф- |
|||
|
|
|
Vк |
Ux |
|||||
|
|
|
p |
|
|
|
|||
|
|
|
Iобр , мА |
|
|
фузионная длина |
дырок |
||
|
|
|
|
|
|||||
|
|
|
|
|
в п-области; ni = 2,5 1019 |
||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
м–3 – концентрация сво- |
|||
|
Рис. 4. ВАХ p-n-перехода |
|
|
бодных электронов. |
|||||
|
|
|
|
|
|
|
|||
26

В связи с тем, что фактическая температура, при которой проводятся измерения, незначительно отличается от T = 300 К, то в расчетах допускается использовать значения параметров собственного полупроводника для T = 300 К.
Примечание. 1. Система уравнений (1) решается следующим образом:
–из второго уравнения определяется численное значения
произведения NdNa и одно из неизвестных, например, Na выражается через второе Nd;
–полученное выражение для Na подставляется в первое уравнение, и в результате получается квадратное уравнение относи-
тельно Nd, которое решается известным способом. 2. Из двух решений системы (1) для сочетаний Nd,Na следует выбрать то, при котором барьерная емкость перехода меньше.
4. Определите суммарное электрическое сопротивление r контактных площадок и пассивных участков p-n-перехода:
r =(Ux −Vк)/Ix, |
(2) |
где Ux, Ix – напряжение и ток в произвольной точке линейного участка прямой ветви вольт-амперной характеристики (см.
рис. 4).
5. Рассчитайте толщину δ(р–п) и барьерную емкость Сδ/u = 0 р-п-перехода по следующим формулам:
δ(р−n) = |
2εε0Vк |
( |
1 |
+ |
1 |
|
), |
(3) |
|
q |
Na |
Nd |
|||||||
|
|
|
|
|
|
где ε = 16 диэлектрическая проницаемость, Ge; ε0 = 8,85·10–12 Ф/м – электрическая постоянная
Cδ/U=0 = εε0S/δ(p−n). |
(4) |
6. Полученные результаты сведите в табл. 3. |
|
|
Таблица 3 |
Рассчитанные параметры р-п-перехода
V |
к, |
В |
N |
а, |
см–3 |
N |
, см–3 |
δ |
(р–п) |
, мкм |
С |
δ / U = 0 |
, пФ |
|
|
|
|
d |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. Содержание отчета
1.Цель работы.
2.Перечень применяемых приборов.
27
3.Электрические схемы исследований.
4.Результаты измерений, расчетов и графики.
5.Выводы.
Контрольные вопросы
1.Чем отличаются равновесные, неравновесные, собственные, примесные, основные и неосновные носители?
2.Какие процессы протекают при формировании р-п-перехо-
да ?
3.Процессы в р-п-переходе при прямом включении?
4.Процессы в р-п-переходе при обратном включении?
5.Что происходит в р-п-переходе при достижении Uпр = Vk?
Рекомендуемая литература
1.Жеребцов И. П. Основы электроники. 5-е изд., перераб. и доп. Л.: Энергоатомиздат, 1989. 352 с.
2.Батушев В. А. Электронные приборы. 2-е изд., перераб. и доп. М: Высш. шк., 1980. 383 с.
Лабораторная работа № 4
ИССЛЕДОВАНИЕ СВОЙСТВ ПОЛУПРОВОДНИКОВ С ПОМОЩЬЮ ЭФФЕКТА ХОЛЛА
Цельработы:определитьзнакзаряда,подвижностьиконцентрацию носителей в полупроводнике с помощью эффекта Холла.
1. Методические указания по подготовке к работе
Эффект Холла относится к гальваномагнитным явлениям, возникающим в твердых телах при действии на них одновременно электрического и магнитного полей. Измерение ЭДС Холла позволяет определить тип носителей заряда и их концентрацию, а в сочетании с измерением проводимости – подвижность носителей заряда. Появление эффекта Холла связано с тем, что на движущийся со скоростью V носитель заряда в магнитном поле с индукцией B действует сила Лоренца FЛ
Л |
[ |
] |
|
F |
=q V ×B , |
(1) |
|
где q = ± 1,601 10–9 Кл (для электрона знак «–», для дырки – «+»).
28
а)
I  B
B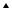
DV
а
UХ |
|
|
C |
|
|
+ |
|
|
+ |
|
|
+ |
|
|
|
+ |
|
F |
|
+ |
|
|
|
FЛ |
|
|
|
|
|
I b
d
б)
I |
|
|
F |
C |
D |
FЛ |
|
B |
|
|
|
|
||
|
+ |
|
|
V |
|
+ |
+ |
||
|
|
|
+ |
|
|
|
а |
+ |
|
|
|
|
||
UХ |
|
|
|
|
|
|
|
|
|
|
d
I b
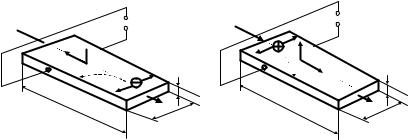
Рис. 1. Эффект Холла в полупроводниках: а – п-типа; б – р-типа
Предположим, что по полупроводнику, имеющему форму прямоугольной пластины, протекает электрический ток I0, (рис. 1,а),обусловленныйдвижениемтолькоэлектронов(полупроводник n-типа). При этом электроны совершают дрейф со скоростью Vв противоположном току I0 направлении. В отсутствии магнитного поля разность потенциалов между точками С и D, лежащими на одной эквипотенциальной поверхности, равна нулю. Если образец поместить в магнитное поле с индукцией B, перпендикулярной направлению тока и плоскости образца, то тогда сила Лоренца будет смещать движущиеся электроны к левой грани пластины. Направление смещения определяется направлением силы Лоренца, т. е. векторным произведением (1) с учетом знака носителей. В результате между боковыми гранями пластины (точками С и D) возникает разность потенциалов (ЭДС Холла).
В полупроводниках р-типа (рис. 1, б) при том же направлении тока вектор скорости дырок направлен в противоположную сторону, знак носителя заряда также другой, и поэтому сила Лоренца (1) действует на дырки в ту же сторону, смещая их также к левой грани. Однако знак ЭДС Холла получается противоположным из-за другого знака носителя.
Накопления носителей заряда у боковой грани пластины прекратиться, когда сила Лоренца уравновесится силой F, действующей на носитель заряда со стороны холловского электрического поля.
При перпендикулярном направлении индукции магнитного поля B к плоскости образца условием равновесия будет равенство
qVB = qEХ, |
(2) |
где EХ – напряженность холловского электрического поля
29
ЭДС Холла, т. е. поперечная разность потенциалов между боковыми гранями пластинки будет
UХ = EХb = VBb, |
(3) |
где b – ширина пластинки.
Для полупроводника р-типа скорость движения дырок V может быть определена из соотношения для плотности тока j
j = qpV, |
(4) |
где p – концентрация дырок.
Подставляя значение V, определенное из (4) в соотношение (3), получим
UХ = |
jBb |
= |
I0Bb |
= |
1 |
|
I0B |
, |
(5) |
qp |
Sqp |
qp |
|
a |
|||||
|
|
|
|
|
|
где S = d b – площадь поперечного сечения пластинки; d – толщина пластинки.
Окончательно получим
UХ = RХ |
I0B |
, |
(6) |
|||
a |
||||||
|
|
|
|
|||
где RХ = 1/qp – постоянная Холла. |
|
|
||||
Для полупроводника п-типа |
|
|
|
|
|
|
RХ = |
1 |
, |
|
(7) |
||
|
|
|||||
|
qn |
|
|
|||
где n – концентрация электронов.
Формулы (6) и (7) выведены из предположения, что энергии, а, следовательно, и скорости всех носителей одинаковы. Это справедливо только для вырожденных полупроводников. В невырожденных полупроводниках носители заряда распределены по скорости, что приводит к появлению в числителе формул (6) и (7) множителя, не равного 1. Для полупроводников с преобладанием рассеяния носителей на тепловых колебаниях кристаллической решетки множитель равен 1,18, для полупроводников с преобладанием рассеяния на ионизированных примесях множитель 1,93. Принято считать, если знак RХ положительный, то основными носителями электрического заряда являются дырки, если знак RХ отрицательный – электроны. Следует отметить, что пропорциональность холловского напряжения индукции магнитного поля сохраняется только в «слабых» магнитных полях.
30
