
МА_технические_семестр1_Пределы Производная Графики Интегралы
.pdf
02.09 |
Вычислить неопределенный интеграл |
|
|
|
|
x |
|
dx. |
|
|
|
|
|
|
|
||||
|
|
x |
2 x2 |
1 |
|||||
|
|
|
|
|
|
||||
02.10 |
Вычислить неопределенный интеграл |
|
|
|
sin xdx |
||||
|
|
|
|
|
|
. |
|||
|
1 |
sin x |
cos x |
||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
dx |
|
|
|
|
|
02.11 |
Вычислить определенный интеграл |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
|
0 |
5 |
|
3sin x |
|
|
|
||
02.12Вычислить несобственный интеграл или доказать его
3
расходимость xdx .
2 4 x2 4
x2 4
02.13Вычислить площадь фигуры, ограниченной параболами
y2=3x, x2=3y.
Вариант № 3
Часть 1. Дифференциальное исчисление
03.01С помощью преобразований на плоскости построить
график функции y |
3x |
5 |
. |
|
|
|
|
|
|
|
|
3x |
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
03.02 |
Вычислить предел |
lim |
5x4 |
|
6x3 |
5 |
|
. |
|||
9 x 2 |
4 |
2x |
|
10 |
|||||||
|
|
|
|
|
x |
|
|
|
|||
03.03Вычислить производные функций
|
|
esin 3x , |
|
|
|
|
|
|
|
1 |
|
|
|
|
||||
a) |
y |
|
b) |
y |
arcsin |
|
x |
|
|
, |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||
|
|
sin 2x |
|
|
|
|
|
|
|
|
|
|||||||
c) |
y |
|
, |
d ) y |
3 |
2x2 ln |
3x 5 , e) x t 0,5sin 2t, y cos3 t. |
|
||||||||||
|
|
|
|
|||||||||||||||
|
2x 3 |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
03.04 |
|
|
|
Вычислить вторую производную функции |
y x3 ln x. |
|||||||||||||
03.05Найти наибольшее и наименьшее значение функции на
заданном промежутке y |
x |
3 |
, [ 5;5]. |
|
x2 |
16 |
|||
|
|
03.06Провести полное исследование и построить график
функции |
y |
x |
1 3 |
. |
|
x |
1 |
2 |
|||
|
|
|
|
||
61

Часть 2. Интегральное исчисление
03.07Вычислить неопределенный интеграл и проверить
dx
результат дифференцированием: .
cos2 5x 3
03.08 |
Вычислить неопределенный интеграл и проверить |
|
|||||||||
результат дифференцированием: |
5x2 3x 2 e2xdx. |
|
|
|
|
|
|
|
|
||
03.09 |
Вычислить неопределенный интеграл |
|
|
|
(2x2 |
13) |
dx. |
||||
|
x |
3 x2 |
4x 5 |
||||||||
|
|
|
|
|
|||||||
03.10 |
Вычислить неопределенный интеграл |
|
|
|
dx |
|
. |
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
cos x(1 sin x) |
|
||||||
|
|
0 |
|
dx |
|
|
|
|
|
|
|
03.11 |
Вычислить определенный интеграл |
|
|
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||||
1 |
3 x |
1 |
|
|
|
||||||
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
03.12Вычислить несобственный интеграл или доказать его
расходимость |
|
dx |
. |
|
|
|
|||
x2 |
4x 5 |
|||
|
|
03.13Вычислить площадь фигуры, ограниченной кривыми
xy=1, x=y, x=2.
Вариант № 4
Часть 1. Дифференциальное исчисление
04.01С помощью преобразований на плоскости построить
график функции y |
4 |
3x |
. |
|
|
|
|
|
x |
1 |
|
|
|
|
|||
|
|
|
|
|
|
|
||
04.02 |
Вычислить предел |
lim |
2x |
1 3x |
||||
|
|
. |
||||||
2x |
3 |
|||||||
|
|
|
|
|
x |
|
|
|
04.03Вычислить производные функций
|
|
|
|
|
|
|
|
|
|
cos2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
x , |
|
||||
a) y |
3 arctg 3 x , b) |
y e |
|
|||||||||||
|
ln |
4x 3 |
|
|
|
|
x3 |
|
5x , e) x 2t4 t, y 8t3 t 2. |
|
||||
c) y |
|
, d ) y |
tg2x |
|
|
|||||||||
|
|
|
|
|
||||||||||
|
|
cos 2x |
|
|
|
|
|
|
||||||
04.04 |
|
|
Вычислить вторую производную функции |
y xarctg2x. |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
62 |
|
|

04.05Найти наибольшее и наименьшее значение функции на
заданном промежутке |
y |
x |
sin x, |
7 |
; |
9 |
. |
|
2 |
2 |
2 |
||||||
|
|
|
|
|
04.06 Провести полное исследование и построить график
функции |
y |
x3 1 |
. |
|
|||
|
|
4x2 |
|
Часть 2. Интегральное исчисление
04.07Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
ex dx |
||
|
|
. |
|
3ex |
6 |
||
|
7 |
|
|
04.08Вычислить неопределенный интеграл и проверить
результат дифференцированием: (x2 2x 1) ln xdx.
04.09Вычислить неопределенный интеграл
04.10Вычислить неопределенный интеграл
x2 |
5x |
6 |
|
dx. |
x4 x2 |
1 x |
|
2 |
|
|
|
dx
3 5cos x .
|
|
|
2 |
04.11 |
Вычислить определенный интеграл cos x sin 3xdx. |
|
0 |
04.12Вычислить несобственный интеграл или доказать его
6 |
|
dx |
|
|
|
расходимость |
|
|
. |
||
|
|
|
|||
|
|
|
|||
3 |
4 x 2 |
||||
2 |
|
|
04.13Вычислить площадь фигуры, ограниченной кривыми
y=ln(x+2), y=2lnx, |
y=0. |
63

Вариант № 5 |
|
|
|
|
||||||
Часть 1. Дифференциальное исчисление |
|
|
|
|||||||
05.01 |
С помощью преобразований на плоскости построить |
|||||||||
график функции y x2 6 |
|
x |
|
10. |
|
3x |
1 5x |
|||
|
|
|
||||||||
05.02 |
Вычислить предел |
lim |
||||||||
|
|
. |
||||||||
3x |
4 |
|||||||||
|
|
|
|
|
|
x |
|
|
|
|
05.03Вычислить производные функций
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) |
y sin |
xe3x , b) |
y |
1 |
x2 arcsin 2x, |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
2 |
5x |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
2 |
|
|
||||
|
|
|
2x |
cos 2x |
|
|
3 |
|
2 |
|
2 |
|
|
||||||||||
c) |
y |
|
|
|
|
, d ) |
y 2 |
|
|
|
|
, e) x |
|
t |
|
|
t |
|
t, y t |
|
|
. |
|
|
tg |
1 |
|
|
|
|
|
3 |
|
2 |
|
|
t |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
05.04 |
|
|
|
|
Вычислить вторую производную функции |
y ectg3x . |
|||||||||||||||||
05.05Найти наибольшее и наименьшее значение функции на
заданном промежутке y |
x |
3 |
, [ 3; 7]. |
x2 |
|
||
|
13 |
||
05.06Провести полное исследование и построить график
функции |
y |
x3 |
|
|
. |
2 x |
1 |
2 |
|||
|
|
|
|
Часть 2. Интегральное исчисление
05.07Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
|
x2dx |
|
. |
|
|
|
||
|
|
|||
|
1 x6 |
|||
05.08 Вычислить неопределенный интеграл и проверить результат дифференцированием: arc sin 2xdx.
05.09Вычислить неопределенный интеграл
05.10Вычислить неопределенный интеграл
x2 |
5 |
dx. |
|
x 1 x2 |
3x 10 |
||
|
dx
sin4 x
.
|
|
|
|
|
2 |
05.11 |
Вычислить определенный интеграл |
x sin 2xdx. |
|
|
0 |
|
64 |
|
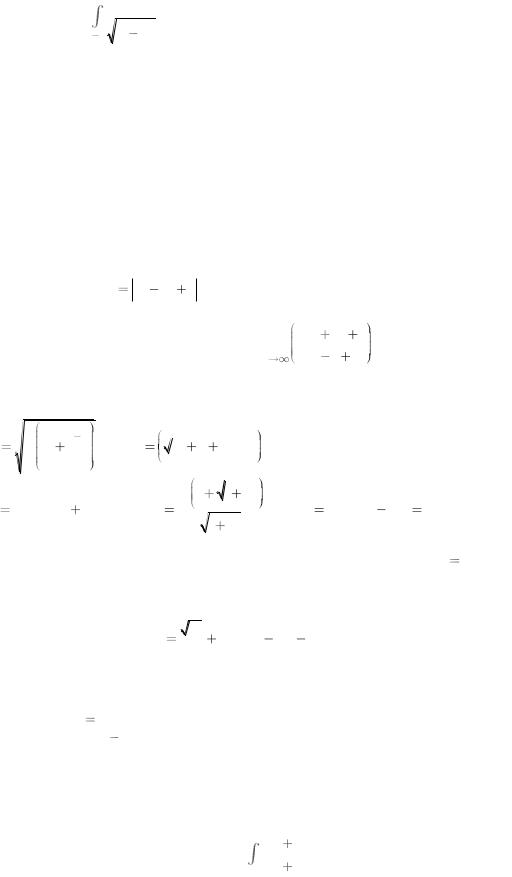
05.12Вычислить несобственный интеграл или доказать его
2 |
|
dx |
|
|
|
расходимость |
|
|
. |
||
|
|
|
|||
|
|
|
|||
x 1 2 |
|||||
1 3 |
|
|
|||
05.13Вычислить площадь фигуры, ограниченной кривой
ρ=acos3 .
Вариант № 6
Часть 1. Дифференциальное исчисление
06.01С помощью преобразований на плоскости построить
график функции y x2 4x 3 .
|
|
|
4x |
2 |
6x |
9 |
x |
06.02 |
Вычислить предел |
|
|
||||
lim |
|
. |
|||||
3x |
2 |
x |
10 |
||||
|
|
x |
|
|
06.03Вычислить производные функций
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
||
|
|
|
x , b) |
|
|
|
|
|
|
2 cos |
|
|
|||||||
a) |
y |
3 ln 3x e |
y |
3x 4 |
|
|
|
, |
|
||||||||||
x |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
ln x |
1 x2 |
|
|
|
|
|
|||||
c) |
y |
arctg2x 5 |
tg3x , |
d ) |
y |
|
|
|
|
|
|
|
, |
e) x arcsin(t2 1), y |
arccos(2t). |
||||
|
|
|
|
|
|
|
|||||||||||||
|
|
x2 |
|||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||||
06.04 |
Вычислить вторую производную функции |
y ex cos x. |
|||||||||||||||||
06.05Найти наибольшее и наименьшее значение функции на
заданном промежутке y |
|
3x |
cos x, [ |
3 |
; |
]. |
|
2 |
2 |
||||||
|
|
|
|
||||
06.06Провести полное исследование и построить график
функции |
y |
|
x |
|
. |
|
|
|
|||
|
x2 |
2 |
|||
|
1 |
|
|
||
Часть 2. Интегральное исчисление
06.07Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
3x |
7 dx |
. |
|
|
||
|
4 |
x2 |
|
65 |
|
|
|

06.08 Вычислить неопределенный интеграл и проверить результат дифференцированием: xarctg4xdx.
06.09Вычислить неопределенный интеграл
06.10Вычислить неопределенный интеграл
x2 |
x 1 |
dx. |
|
x3 x |
1 2 |
||
|
dx
cos6 x
.
|
|
3 |
|
|
06.11 |
Вычислить определенный интеграл |
x2 9 x2 dx. |
||
|
|
3 |
|
|
06.12Вычислить несобственный интеграл или доказать его
расходимость |
|
ln x |
dx. |
|
|
||
|
1 |
x3 |
|
|
|
|
|
06.13 Вычислить площадь фигуры, ограниченной кривой
ρ=a(cos +sin ).
Вариант № 7
Часть 1. Дифференциальное исчисление
07.01С помощью преобразований на плоскости построить
график функции y 5 x x2.
|
|
|
|
|
|
|
07.02 |
Вычислить предел |
lim x2 3x 5 x2 8x 4 . |
||||
|
|
x |
||||
07.03Вычислить производные функций
|
|
|
|
|
|
|
|
|
|
|
|
3 2x3 |
|
|
|
|
|
a) y |
4 3x |
2 |
5x |
6 |
, b) y tg |
|
x |
, |
|
||||||||
|
x |
|
5 |
3x2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
c) y |
ln |
|
2x |
3 |
, d ) |
|
y |
sin x |
, e) |
x t 2 t 1, y t3 t. |
|
||||||
|
3x |
4 |
|
ecos 2x |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
07.04 |
|
|
|
|
Вычислить вторую производную функции |
y e2x sin x. |
|||||||||||
07.05Найти наибольшее и наименьшее значение функции на
заданном промежутке y |
x |
5 |
, [ 3;7]. |
x2 |
|
||
|
11 |
||
66

07.06Провести полное исследование и построить график
функции |
y |
x2 x |
|
1 |
. |
|
x |
1 |
2 |
||||
|
|
|
||||
|
|
|
|
Часть 2. Интегральное исчисление
07.07Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
4x2 |
29 |
9 xdx. |
07.08Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
x cos x |
dx. |
|
||
|
sin3 x |
|
07.09Вычислить неопределенный интеграл
07.10Вычислить неопределенный интеграл
2x2 |
x |
4 |
|
dx. |
x3 x2 |
4x |
|
4 |
|
|
|
cos3 xdx . 5 sin2 x
|
|
|
|
|
|
|
|
2 |
|
|
dx |
|
|
07.11 |
Вычислить определенный интеграл |
|
|
. |
||
|
|
|
||||
1 |
sin x cos x |
|||||
|
0 |
|
||||
07.12Вычислить несобственный интеграл или доказать его
1
расходимость dx .
0 x3 5x2
07.13 Найти длину дуги полукубической параболы y2=x3 от начала координат до точки с абсциссой x=5.
|
Вариант № 8 |
|
|
|
|
|
|
|
||||||
Часть 1. Дифференциальное исчисление |
|
|
|
|
|
|||||||||
08.01 |
С помощью преобразований на плоскости построить |
|||||||||||||
график функции y |
|
5 |
|
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||||
08.02 |
Вычислить предел |
lim |
|
x3 27 |
|
x2 9 |
. |
|||||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x 3 |
sin x |
3 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
08.03Вычислить производные функций
67

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 2x3 |
3 |
|
|
|
|
|
|
|
|
tg2x |
|
|
|
|
|
||||
a) |
y |
|
|
x , |
b) |
y |
|
, |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x2 |
|
|
|
|
|
|
|||||||||||||||
|
1 |
x2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
c) |
y |
1 |
arcsin 2x, |
d ) y |
cos |
3 |
|
e x , |
e) x ctgt, y |
1 |
. |
|
|||||||||
|
|
|
|
|
|||||||||||||||||
|
|
x |
|
|
|
|
|
|
x |
|
|
|
|
|
|
cos2 t |
|
||||
08.04 |
|
|
|
Вычислить вторую производную функции |
y e x sin x. |
||||||||||||||||
08.05Найти наибольшее и наименьшее значение функции на
заданном промежутке |
y 2tgx tg2 x, 0; |
. |
|
|
3 |
08.06Провести полное исследование и построить график
функции |
y |
|
x |
|
. |
|
|
|
|||
|
|
|
|||
|
|
3 x2 |
1 |
|
|
Часть 2. Интегральное исчисление |
|||||
08.07 |
Вычислить неопределенный интеграл и проверить |
||||
результат дифференцированием: 3 3 6x5 x4dx.
3 6x5 x4dx.
08.08Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
|
|
dx |
|
|
. |
|
|
|
|
|
||
|
|
|
|
|
||
1 |
|
ex |
||||
08.09Вычислить неопределенный интеграл
08.10Вычислить неопределенный интеграл
8
08.11Вычислить определенный интеграл
3 1
|
dx |
|
. |
|
||
|
|
|
|
|||
x3 |
8 |
|||||
|
|
|
||||
sin x |
|
|
2 cos x 3 |
dx. |
||
|
|
|
|
|
||
3 sin x 2 cos x |
||||||
dx |
|
|
. |
|
||
|
|
|
|
|||
|
x |
1 |
|
|||
08.12Вычислить несобственный интеграл или доказать его
расходимость |
|
dx |
|
. |
|
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
1 1 |
x x |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
|
x |
|
|
|
|
|
|
|
y e2 |
e 2 |
|||
08.13 |
Найти длину цепной линии |
|
|
от точки x=0 до |
||||||
точки |
x=2. |
|
|
|
|
|
|
|
|
|
68

Вариант № 9 |
|
|
|
|
|
|||
Часть 1. Дифференциальное исчисление |
|
|
|
|
||||
09.01 |
С помощью преобразований на плоскости построить |
|||||||
график функции y |
|
|
|
|
|
|
|
|
3x 5. |
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
09.02 |
Вычислить предел |
lim |
2x 9 x 3 |
. |
||||
|
||||||||
|
|
|
|
x 0 |
|
2x |
||
|
|
|
|
|
|
|
|
|
09.03Вычислить производные функций
|
|
3 |
|
|
|
x |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 4 |
|
arc co s 4 x3 , |
|
|
|
|
|
|
|
|
||||||
a) |
y sin |
|
cos |
|
, |
b) |
tg 4x |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
5x |
e |
3x |
|
|
|
|
|
|
|
|
2 |
t |
|
t |
2 |
|
|
|
||||
c) |
y |
|
, d ) |
|
y |
arctg2x arcctg3x, e) x |
, y |
|
. |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
ln x |
|
|
2 |
t2 |
2 |
t2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
09.04 |
|
|
|
Вычислить вторую производную функции |
|
|
|
|
||||||||||||||||
|
|
|
|
y x 1 x2 . |
||||||||||||||||||||
09.05Найти наибольшее и наименьшее значение функции на
заданном промежутке y |
x3 9x |
, [ 2; 1]. |
|
10 |
|||
|
|
09.06Провести полное исследование и построить график
функции |
y |
x |
1 3 |
. |
|
x |
2 |
2 |
|||
|
|
|
|
||
Часть 2. Интегральное исчисление
09.07Вычислить неопределенный интеграл и проверить
результат дифференцированием: earctgx2 |
|
xdx |
. |
|
|
||
1 |
x4 |
||
09.08Вычислить неопределенный интеграл и проверить
|
|
|
|
|
|
результат дифференцированием: |
1 |
|
x2 |
||
|
|
|
|
dx. |
|
|
|
x2 |
|
||
|
|
|
|
|
|
09.09Вычислить неопределенный интеграл
09.10Вычислить неопределенный интеграл
2x2 |
5x |
6 |
dx. |
|
x2 |
4 x2 |
2 |
||
|
dx |
. |
|
|
||
sin2 x 2sin x cos x 12 cos2 x |
||
|
16
09.11Вычислить определенный интеграл
0
dx |
. |
|
|
x 9 |
x |
69

09.12Вычислить несобственный интеграл или доказать его
расходимость |
|
dx |
|
|
|
. |
|
1 |
x ln3 x |
||
|
|
|
|
09.13 Вычислить длину дуги кардиоиды ρ=a(1+cos ).
Вариант № 10
Часть 1. Дифференциальное исчисление
10.01С помощью преобразований на плоскости построить
график функции y 
 6 5x.
6 5x.
|
|
|
ln e2x2 |
sin 6x |
||
10.02 |
Вычислить предел |
lim |
|
|
|
. |
ln e3x |
2 |
|
||||
|
|
x |
|
co s 5x |
||
10.03Вычислить производные функций
a) |
y |
arc sin x |
arc cos x 10 , |
b) |
|
y |
|
|
ln 2x |
|
, |
|
||||||
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 1 |
|
|||
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
ctg |
|
, d ) |
|
|
|
x2 arctgx, e) x 2 cos3 2t, y sin3 |
|
||||||
c) |
y |
e x |
y |
1 |
2t. |
|||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|||
10.04 |
|
|
Вычислить вторую производную функции |
y x sin2 x. |
||||||||||||||
10.05Найти наибольшее и наименьшее значение функции на
заданном промежутке y |
x2 |
1 |
, |
[ |
1 |
; 2]. |
|
2 |
|
x |
2 |
||||
|
|
|
|
|
|||
10.06Провести полное исследование и построить график
функции |
y x arctgx. |
Часть 2. Интегральное исчисление
10.07Вычислить неопределенный интеграл и проверить
результат дифференцированием: |
|
ex dx |
|
. |
||
|
|
|
|
|||
1 |
e2x |
|||||
|
|
|
||||
10.08Вычислить неопределенный интеграл и проверить
результат дифференцированием:
70
3x 5 dx

 x2 6x 10
x2 6x 10
.
