7) Оценка погрешности аппроксимации.

Рассчитаем по формуле (3.7) значения аппроксимирующей функции в заданных точках xi (i=1, …, 5) и соответствующие отклонения (табл. 4).

Таблица 3.5

xi	3,0	4,0	5,0	6,0	7,0	8,0
yi	3,22	4,21	4,85	5,63	4,77	4,2
φ(xi)	3,076	4,470	5,054	5,127	4,847	4,308
	0,143	0,260	0,205	0,501	0,078	0,109

В соответствии с табл. 3.5 построим графики исходной и аппроксимирующей функций (рис. 3.1).

Рис. 3.1

Вычислим значение критерия аппроксимации, подставив в (2.2) данные из табл. 3.5 получим (3.8).

(3.8)

Максимальное по модулю отклонение при .

4 Схема алгоритма программы:

Начало

Вывод("Диалоговый комментарий")

i=0…n-1

Ввод (x_i,y_i)

i

Расчет значений коэффициентов системы уравнений

Решение системы уравнений методом

Гаусса

Вычисление значений Yl, D, Kr, Dmax и IM

Вывод("Диалоговый комментарий")

1

Начало

да

к = 0

Возврат 1

нет

к = 1

да

нет

Возврат ln(x_i)

Возврат x_i

Конец

Cхема алгоритма функции FI( k, x[i] )

5 Код программы:

#include <stdio.h>

#include <math.h>

#include <conio.h>

#include <stdlib.h>

#define m 3

#define n 6

void Massiv(float *M,char *Name,int x)

{

int i,j;

printf("Array %s:\n",Name);

for (j=0;j<x;j++)

{

printf ("%5.3f\t",M[j]);

}

printf ("\n");

}

void znachenia (float X[n],float Y[n])

{

int i;

printf("vvedite:\n");

for (i=0;i<n;i++)

{

printf ("X[%i]=",i+1);

scanf ("%f",&X[i]);

printf ("Y[%i]=",i+1);

scanf ("%f",&Y[i]);

}

}

float F1(int k, float N)

{

if (k==0) return 1;

if (k==1) return log(N);

else

return N;

}

void koefficent (float A[m][m], float B[m], float X[n], float Y[n])

{

int i,l,k;

for (i=0;i<m;i++)

for (l=0;l<m;l++)

{

A[i][l] = 0;

for (k=0;k<n;k++)

A[i][l]=A[i][l] + F1(i,X[k]) * F1(l,X[k]);

}

for(k=0;k<m;k++)

{

B[k] = 0;

for (i=0;i<n;i++)

B[k]=B[k]+Y[i]*F1(k,X[i]);

}

}

int ved(float A[m][m], int i)

{

int g, h, k;

float MaxA;

h = -1;

MaxA = 0;

for(k=i;k<m;k++)

if(fabs(A[k][i])>fabs(MaxA))

{

MaxA = A[k][i];

h = k;

}

if(h == -1)

{

printf("Matrix virogdena\n");

abort ();

}

return h;

}

void perest (float A[m][m],float B [m],int i,int IM)

{

float temp; int j;

if(IM !=i)

{

for (j=i;j<m;j++)

{

temp = A[i][j];

A[i][j] = A[IM][j];

A[IM][j] = temp;

}

temp = B[i];

B[i] = B[IM];

B[IM] = temp;

}

}

void rkoef(float A[m][m],float B[m],int i,int l)

{

int j; float Q;

Q=A[l][i] / A[i][i];

A[l][i] = 0;

for (j=i+1;j<m;j++)

A[l][j] = A[l][j] - Q*A[i][j];

B[l]=B[l] - Q*B[i];

}

void prgauss(float A[m][m],float B[m])

{

int i, IM, l, j;float Q;

for(i=0;i<m;i++)

{

IM = ved(A, i);

perest(A, B, i, IM);

for(l=i+1;l<m;l++)

rkoef(A, B, i, l);

}

for (i=0;i<m;i++)

{

for (j=0;j<m;j++)

printf(" %f ", A[i][j]);

printf("\n");

}

}

void obrgauss(float A[m][m],float B[m],float C[m])

{

int k,j;float Sum;

C[m-1] = B[m-1] / A[m-1][m-1];

for(k = m - 2;k>=0;k--)

{

Sum = B[k];

for(j=k+1;j<m;j++)

Sum = Sum - A[k][j]*C[j];

C[k] = Sum / A[k][k];

}

}

void apr(float C[m],float X[n],float Y[n],float Y1[n],float D[n],float *Kr)

{

int i;

*Kr=0;

for (i=0;i<n;i++)

{

Y1[i]=C[0]*F1(0,X[i])+C[1]*F1(1,X[i])+C[2]*F1(2,X[i]);

D[i]=fabs(Y[i]-Y1[i]);

*Kr=*Kr+D[i]*D[i];

}

}

void krappr(float D[n],float *Dmax, int *IM)

{

int i;

*Dmax=D[0];

*IM=0;

for(i=0;i<n;i++)

if(fabs(D[i])>fabs(*Dmax))

{

*Dmax=D[i];

*IM=i;

}

}

void vivodvsego(float C[m],float X[n],float Y1[n],float D[n],float Kr,float Dmax,int IM)

{

Massiv(C, "C", m);

Massiv(Y1, "Y1", n);

Massiv(D, "D", n);

printf("Dmax = %5.3f pri X[%i] = %5.3f\n",Dmax,IM+1,X[IM]);

printf("Kr = %5.4f\n",Kr);

}

int main()

{

float X[n],Y[n],A[m][m],B[m],C[m],Y1[n],D[n],Dmax,Q,Kr,Sum;

int i, j, IM;

znachenia(X, Y);

koefficent(A, B, X, Y);

printf("Massiv A\n");

for(i=0; i<m; i++)

{

for(j=0; j<m; j++)

printf(" %f ", A[i][j]);

printf("\n");

}

Massiv(B, "B", m);

prgauss(A, B);

obrgauss(A, B, C);

apr(C, X, Y, Y1, D, &Kr);

krappr(D, &Dmax, &IM);

vivodvsego(C, X, Y1, D, Kr, Dmax, IM);

getch();

return 0;

}

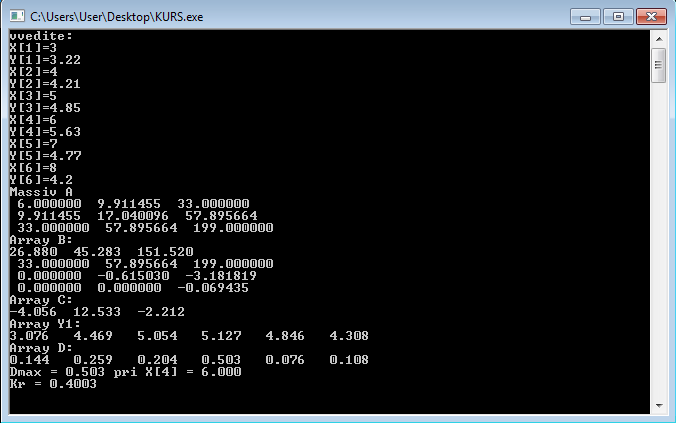
6 Результаты машинного счета

6.1 Исходные данные

Таблица 6.1

x	3,0	4,0	5,0	6,0	7,0	8,0
y	3,22	4,21	4,85	5,63	4,77	4,2

6.2 Результаты

Коэффициенты:

С₁ = -4,056

С₂ = 12,533

С₃ = -2,212

Таблица 6.2

Значения аппроксимирующей функции	Значения отклонений по абсолютному значению
3,076	0,144
0,469	0,259
5,054	0,204
5,127	0,503
4,846	0,076
4,308	0,108

Максимальное отклонение 0,503 при x₄=6,0, значение критерия аппроксимации 0,400.

7 Вывод: цель достигнута.

Поставленные в начале работы задачи выполнены, данные, полученные в ручном счете, совпадают с данными, полученными с помощью программы, с точностью до 0,001.

В ходе выполнения курсовой работы были решены типовые инженерные задачи обработки данных, используя методы матричной алгебры, и решал системы линейных алгебраических уравнений. Навыки, приобретённые в процессе выполнения курсовой работы, являются основой для использования вычислительных методов прикладной математики и техники программирования в процессе изучения всех последующих дисциплин, а также при выполнении курсовых и дипломных проектов.

В ходе данной работы:

1. Освоены типовые вычислительные методы прикладной математики;

2. Усовершенствованы навыки разработки алгоритмов и построения программ на языке высокого уровня;

3. Усовершенствованы принципы модульного программирования и техники использования подпрограмм.

25