
- •1 Цель работы
- •2 Методические указания
- •2.1 Методические рекомендации по аппроксимации методом наименьших квадратов
- •2.1.1 Постановка задачи
- •2.2 Методика выбора аппроксимирующей функции
- •2.3 Общая методика решения
- •2.4 Методика решения нормальных уравнений
- •2.5 Оценка погрешности аппроксимации
- •3 Ручной счёт
- •3.1 Табличное представление исходных данных
- •3.2. Критерий аппроксимации
- •7) Оценка погрешности аппроксимации.
- •5 Код программы:
2.5 Оценка погрешности аппроксимации
Результатом этапа решения системы нормальных уравнений (2.6) является получение значений параметров аппроксимирующей функции для заданного набора базисных аппроксимирующих функций
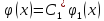 +
+
 ,….,
,….,
Решение
( )
системы нормальных уравнений определяет
значения параметров, при которых критерий
качества аппроксимации J принимает
минимально возможное значение
)
системы нормальных уравнений определяет
значения параметров, при которых критерий
качества аппроксимации J принимает
минимально возможное значение При всех других допустимых значениях
параметров величина критерия будет
больше. тем самым полученное значение
При всех других допустимых значениях
параметров величина критерия будет
больше. тем самым полученное значение может быть принято за характеристику
эффективности аппроксимации заданной
функциональной зависимости функциями
может быть принято за характеристику
эффективности аппроксимации заданной
функциональной зависимости функциями
 выбранного
класса. При изменении класса аппроксимирующих
функций, а также при изменении набора
базисных функций значение
выбранного
класса. При изменении класса аппроксимирующих
функций, а также при изменении набора
базисных функций значение
 может
меняться. Сравнение различных классов
функций по их эффективности (качеству)
аппроксимации может осуществляться на
основе сравнений соответствующих
значений
может
меняться. Сравнение различных классов
функций по их эффективности (качеству)
аппроксимации может осуществляться на
основе сравнений соответствующих
значений .
.
Для
количественной оценки погрешности
аппроксимации может использоваться
также величина (Δ)
максимального отклонения исходной
функциональной зависимости от найденной
аппроксимирующей. Для этого определяется
отклонение
 во
всех заданных точках и определяется
максимальное из этих отклонений:
во
всех заданных точках и определяется
максимальное из этих отклонений:
![]()
|
(2.12) |
3 Ручной счёт
3.1 Табличное представление исходных данных
Таблица 3.1
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
|
xi |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
|
yi |
3.22 |
4.21 |
4.85 |
5.63 |
4.77 |
4.2 |
3.2. Критерий аппроксимации
1) Запишем выражение (3.1) для критерия аппроксимации:
J
= min
 [yi
– С1
– C2*ln(xi)
– C3*xi]².
(3.1)
[yi
– С1
– C2*ln(xi)
– C3*xi]².
(3.1)
2)
В соответствии с условиями локального
минимума функции J(C1,
C2,
C3)
найдем частные производные
 (18),
(18),
 (19),
(19),
 (20) и приравняем их к нулю:
(20) и приравняем их к нулю:
 =
= 2((yi–С1–ln(xi
2((yi–С1–ln(xi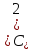 -xi*
-xi* )×(-1))=
-2
)×(-1))=
-2 (yi–С1–ln(xi)*
(yi–С1–ln(xi)* -xi*
-xi* )=0
(3.2)
)=0
(3.2)
 =
= 2((yi–С1–ln(xi
2((yi–С1–ln(xi )
) (-ln(xi)))=
(-ln(xi)))=
=
-2 (yi*ln(xi)–ln(хi)*С1–ln2(xi)
(yi*ln(xi)–ln(хi)*С1–ln2(xi) -хi*ln(xi)
-хi*ln(xi) )=0
(3.3)
)=0
(3.3)
 =
= 2((yi
– С1– ln(xi
2((yi
– С1– ln(xi -xi*
-xi* )
) (-xi))=
(-xi))=
=
-2 (yi*xi
– C1*xi
– xi*ln(xi)
(yi*xi
– C1*xi
– xi*ln(xi) -
xi2*
-
xi2* )=
0
(3.4)
)=
0
(3.4)
3) Приведем полученную систему уравнений к нормальному виду (3.5), перенеся свободные члены вправо и поделив обе части на 2.
6C1
+ C2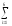 ln(xi)+
C3
ln(xi)+
C3 xi
=
xi
=
 yi
yi
C1 ln(xi)+
C2
ln(xi)+
C2 ln2(xi)+
C3
ln2(xi)+
C3 xi×ln(xi)=
xi×ln(xi)=
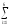 ln(xi)
ln(xi) yi
(3.5)
yi
(3.5)
C1 xi
+ C2
xi
+ C2 ln(
xi)×xi
+ C3
ln(
xi)×xi
+ C3
 xi2
=
xi2
=
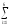 xi
xi yi
yi
4) Для удобства представим промежуточные результаты вычислений в виде таблицы:
Таблица 3.2
|
x[i] |
y[i] |
ln(x[i]) |
x*x |
y[i]*x[i] |
x[i]*ln(x[i]) |
y*ln(x[i]) |
lnx[i]*lnx[i] |
|
3 |
3,22 |
1,098612289 |
9 |
9,66 |
3,295836866 |
3,53753157 |
1,20694896 |
|
4 |
4,21 |
1,386294361 |
16 |
16,84 |
5,545177444 |
5,83629926 |
1,92181206 |
|
5 |
4,85 |
1,609437912 |
25 |
24,25 |
8,047189562 |
7,805773875 |
2,59029039 |
|
6 |
5,63 |
1,791759469 |
36 |
33,78 |
10,75055682 |
10,08760581 |
3,210402 |
|
7 |
4,77 |
1,945910149 |
49 |
33,39 |
13,62137104 |
9,281991411 |
3,78656631 |
|
8 |
4,2 |
2,079441542 |
64 |
33,6 |
16,63553233 |
8,733654475 |
4,32407713 |
|
33 |
26,88 |
9,911455722 |
199 |
151,52 |
57,89566406 |
45,2828564 |
17,0400968 |
5) Используя значения из табл. 3.2, запишем систему уравнений (3.5) в окончательном виде (3.6):
6С1 + 9,911C2 + 33C3 =26,88
9,911C1 + 17,04C2 + 57,896C3 = 45,28 (3.6)
33C1 + 57,896C2 + 199C3 = 151,52
Полученную систему уравнений решаем методом Гаусса.
Таблица 3.3
|
Матрица 1 |
|||
|
6,000 |
9,911 |
33 |
26,88 |
|
9,911 |
17,04 |
57,896 |
45,28 |
|
33 |
57,896 |
199 |
151,52 |
|
Коэффициенты |
|
|
С1 |
-4,056 |
|
С2 |
12,533 |
|
С3 |
-2,212 |
Таблица 3.4
6)
В результате решения исходной системы
линейных уравнений и нахождения значений
 получаем запись искомой аппроксимирующей
функции в следующем виде (3.7):
получаем запись искомой аппроксимирующей
функции в следующем виде (3.7):
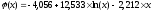 .
(3.7)
.
(3.7)
