Пример вычисления корреляции
Имеем следующие данные:
U1 U2
-0,120 -0,691
-0,117 -0,694
-0,120 -0,696
-0,120 -0,691
-0,120 -0,694
-0,120 -0,691
-0,120 -0,696
-0,120 -0,698
-0,112 -0,667
-0,107 -0,657
-0,107 -0,647
-0,107 -0,642
-0,103 -0,637
Перед тем как
перейти к подсчету корреляции, необходимо
найти для каждого столбца среднее
значение (
и
)
и дисперсию. Среднее значение находится
по формуле:
(1)
Дисперсия находится по формуле:
(2),
где
-
среднее переменной
,
-
среднее переменной
.
В данном
примере
=
-0,11458, а
=
-0,677.
Отсюда
Корреляция рассчитывается по формуле:
(3),
Подставляя данные в формулу (3) получим:
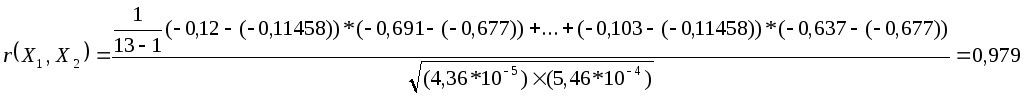
Пример построения линейной регрессии
При рассмотрении данного примера используются те же данные, что и при подсчете корреляции.
Регрессионная модель описывается следующим уравнением:
,
(4)
где a– пересечение линии регрессии с осьюy;b– угол наклона линии регрессии (коэф. регрессии).
Формулы для определения угла наклона линии регрессии и её пересечения с осью OYследующие:
, (5)
где n– размер выборки
, (5)
Данные для расчета линии регрессии представлены в таблице 1
Таблица 1
|
X2 |
X1 |
X1*X2 |
X12 |
|
-0,691 |
-0,12 |
0,08292 |
0,0144 |
|
-0,694 |
-0,117 |
0,081198 |
0,013689 |
|
-0,696 |
-0,12 |
0,08352 |
0,0144 |
|
-0,691 |
-0,12 |
0,08292 |
0,0144 |
|
-0,694 |
-0,12 |
0,08328 |
0,0144 |
|
-0,691 |
-0,12 |
0,08292 |
0,0144 |
|
-0,696 |
-0,12 |
0,08352 |
0,0144 |
|
-0,698 |
-0,12 |
0,08376 |
0,0144 |
|
-0,667 |
-0,112 |
0,074704 |
0,012544 |
|
-0,657 |
-0,107 |
0,070299 |
0,011449 |
|
-0,647 |
-0.107 |
0,069229 |
0,011449 |
|
-0,642 |
-0.107 |
0,068694 |
0,011449 |
|
-0,637 |
-0.103 |
0,065611 |
0,010609 |
|
Итого: -8.801 |
--1,493 |
1,012575 |
0,171989 |
Подставив, данные из таблицы в формулу (5) и (6) получим:
Подставим
полученные значения в формулу (4):
Построим
график этой функции.
Полученные данные сравнить с результатами, полученными в программе “VoltNew”
Для упрощения вычислений и построения графиков, рекомендуется пользоваться MSExcel.
Лабораторная работа №4
Цель работы:ознакомление с системой“MatLab”.
В предыдущей лабораторной работе, была рассмотрена программа “VoltNew” для работы с данными. Эта программа обладает ограниченными возможностями, поэтому необходимо уметь пользоваться другими средствами для обработки данных.
MATLAB– это высокопроизводительный язык для технических расчетов. Он включает в себя вычисления, визуализацию и программирование в удобной среде.
Наиболее известные области применения системы MATLAB:
математика и вычисления;
разработка алгоритмов;
вычислительный эксперимент, имитационное моделирование, макетирование;
анализ данных, исследование и визуализация результатов;
научная и инженерная графика;
разработка приложений, включая графический интерфейс пользователя.
Слово MATLABозначает матричная лаборатория (matrixlaboratory)
MATLAB - это интерактивная система, основным объектом которой является массив, для которого не требуется указывать размерность явно. Это позволяет решать многие вычислительные задачи, связанные с векторно-матричными формулировками, существенно сокращая время, которое понадобилось бы для программирования на скалярных языках типа C или FORTRAN.
В методических указаниях не будут рассмотрены все возможности MATLAB и поэтому описаны будут те команды, которые понадобятся в ходе выполнения лабораторной работы.
1.1. Командное окно. Инструментальная панель
К
омандное
окно системы MATLAB показано на рис. 1. Здесь
же показано ниспадающее меню File.
Оно содержит следующие опции:
|
Опция |
Подопции |
Назначение |
|
New |
M-file Figure |
Открыть в редакторе/отладчике новый файл Открыть графическое окно |
|
Open |
|
Открыть в редакторе/отладчике указанный файл |
|
Open Selection |
|
Открыть в редакторе/отладчике файл, выделенный в произвольной строке командного окна |
|
Run Script |
|
Вызов окна для запуска Script-файла |
|
Load Workspace |
|
Вызов окна загрузки МАТ-файла |
|
Save Workspace As |
|
Вызов окна сохранения МАТ-файла |
|
Show Workspace |
|
Вызов средства просмотра рабочей области Workspace Browser |
|
Set Path |
|
Вызов средства просмотра путей доступа Path Browser |
|
Preferences |
|
Выбор характеристик |
|
Print Setup |
|
Установка опций принтера |
|
|
|
Установка опций вывода на печать |
|
Print Selection |
|
Печать выделенного фрагмента |
Особого рассмотрения заслуживает опция Preferences (Выбор характеристик), которая включает 3 окна. В первую очередь, рассмотрим окно General (Общее) (рис. 2).
В этом окне можно видеть 3 поля и 3 маркера, имеющие следующие назначения:
|
Формат данных |
Назначение |
|
Numeric Format |
Выбор формата представления чисел и межстрочного пробела. По умолчанию, формат Short, пробел Loose |
|
Editor Preference |
Выбор текстового редактора По умолчанию, встроенный редактор Built in Editor |
|
Help Directory |
Каталог справки Help |
|
Echo on |
Показывать на экране команды исполняемого Script-файла сценария/Не показывать |
|
Show Toolbar |
Показывать на экране инструментальную панель/Не показывать |
|
Enable Graphical Debugging |
Поддерживать отладку графики/Не поддерживать |
Инструментальная панель.
Инструментальная панель командного окна системы MATLAB позволяет обеспечить простой доступ к операциям над М-файлами (рис. 3)
|
New File |
Open File |
Cut |
Copy |
Paste |
Undo |
Workspace Browser |
Path Browser |
Help |
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
Эти операции включают:
создание нового М-файла (New File);
открытие существующего М-файла (Open File);
удаление фрагмента (Cut);
копирование фрагмента (Copy);
вставка фрагмента (Paste);
восстановление только выполненной операции (Undo);
просмотр рабочей области (Workspace Browser);
просмотр путей доступа (Path Browser);
текущая помощь (Help)