
Экономика профиль Финансы (1 семестр) ФДПО / Контрольная работа по линейной алгебре
.docКОНТРОЛЬНАЯ РАБОТА ПО ЛИНЕЙНОЙ АЛГЕБРЕ
Рекомендации по выполнению и оформлению контрольных работ
Контрольная работа – письменная работа студента, включающая изучение теоретических основ дисциплины и умение анализировать практические ситуации.
Перед выполнением контрольной работы студент должен изучить соответствующие разделы курса “Математика”, используя учебную литературу. Список рекомендуемой литературы приведен в методических указаниях. Студент может использовать также учебники и учебные пособия, не включенные в данный список, а также ресурсы Интернет.
Представленная для рецензирования контрольная работа должна содержать все задачи, указанные преподавателем. Решения задач следует приводить в той последовательности, которая определена в таблице вариантов. Условие каждой задачи должно быть приведено полностью перед ее решением.
Зачет по контрольной работе выставляется по результатам рецензирования и является обязательным для допуска к сдаче зачетов и экзаменов, которые предусмотрены учебным планом.
Контрольная работа выполняется по варианту, номер которого совпадает с последней цифрой шифра зачетной книжки студента. В таблице приведены номера задач.
|
Вариант |
Контрольная работа |
|
01 |
1 11 21 31 41 51 61 71 |
|
02 |
2 12 22 32 42 52 62 72 |
|
03 |
3 13 23 33 43 53 63 73 |
|
04 |
4 14 24 34 44 54 64 74 |
|
05 |
5 15 25 35 45 55 65 75 |
|
06 |
6 16 26 36 46 56 66 76 |
|
07 |
7 17 27 37 47 57 67 77 |
|
08 |
8 18 28 38 48 58 68 78 |
|
09 |
9 19 29 39 49 59 69 79 |
|
10 |
10 20 30 40 50 60 70 80 |
|
|
|
Задача 1.
1-10. Исходя из определения равенства множеств и операций над множествами, доказать тождество и проверить его с помощью диаграммы Эйлера – Венна.
-
A \ (B C) = (A \ B) (A \ C) .
-
A (B (A C)) = (A B) (A C) .
-
A (B (A C)) = (A B) (A C) .
-
A (B C) = (A B) (A C) .
-
A (B C) = (A B) (A C) .
-
A \ B = A \ (A B) .
-
A (B C) = (A B) C .
-
A (B C) = (A B) C .
-
A (B C) = (A B) (A C) .
-
(A \ B) \ C =(A \ C) \ B .
Задача 2.
11-20. Решить систему линейных уравнений по формулам Крамера и методом обратной матрицы.
11.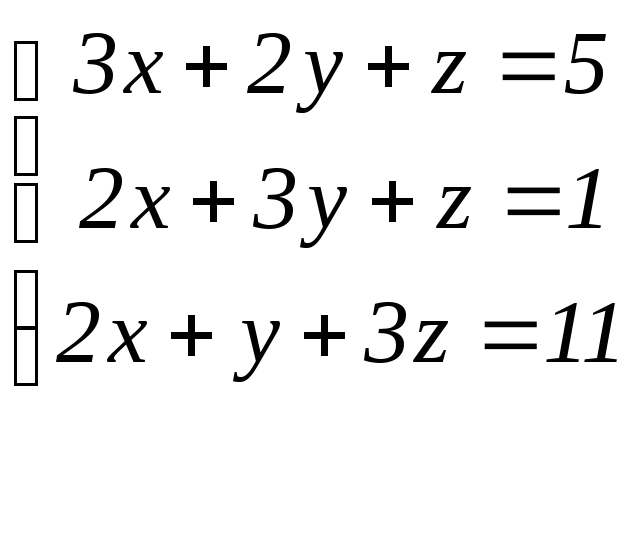 16.
16.
12. 17.
17.

13.
 18.
18.

14.
 19.
19.

15.
 20.
20.

Задача 3.
21-30. Исследовать систему на совместность. Применяя метод Гаусса, решить систему линейных уравнений. Сделать проверку найденного решения.
21. 22.
22.

23.
 24.
24.

25.
 26.
26.
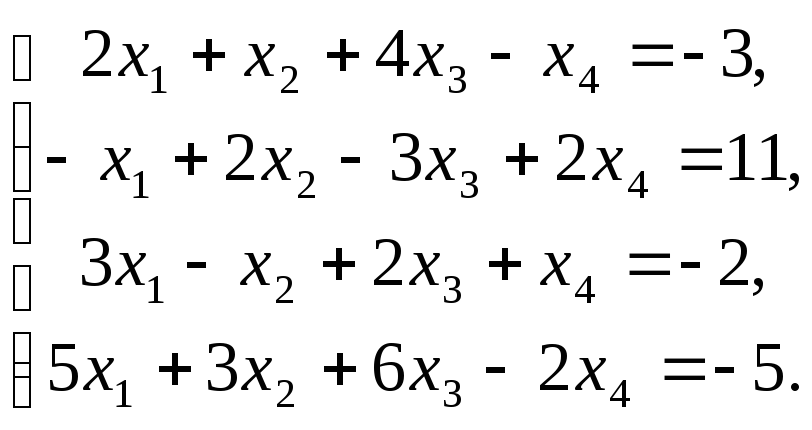
27.
 28.
28.
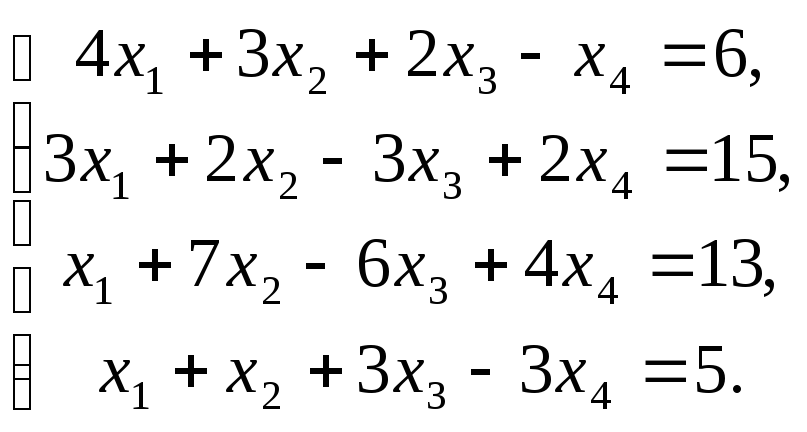
29.
 30.
30.

Задача 4.
31-40. Даны вершины А(х1;у1); В(х2;у2); С(х3;у3) треугольника АВС. Найти
1) длину стороны ВС;
2) величину внутреннего угла А;
3) уравнение стороны ВС;
4) уравнение медианы; проведенной из вершины В;
5) площадь треугольника АВС;
6) уравнение высоты; проведённой через вершину А;
7) точку пересечения медианы ВМ и высоты АН.
31. А (-5;-5), В(-3;0), С(0;-5);
32. А (-5;-4), В(-3;1), С(0;-4);
33. А (-5;-3), В(-3;2), С(0;-3);
34. А (-5;-2), В(-3;3), С(0;-2);
35. А (-5;-1), В(-3;4), С(0;-1);
36. А (-5;0), В(-3;5), С(0;0);
37. А (-5;1), В(-3;6), С(0;1);
38. А (-5;2), В(-3;7), С(0;2);
39. А (-5;3), В(-3;8), С(0;3);
40. А (-5;4), В(-3;9), С(0;4);
Задача 5.
41-50. Даны векторы
![]() в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы
![]() образуют базис, и найти координаты
вектора
образуют базис, и найти координаты
вектора
![]() в этом базисе.
в этом базисе.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 6.
51-60. Найти собственные значения и собственные векторы матрицы А.
51.
 52.
52.

53.
 54.
54.

55.
 56.
56.

57.
 58.
58.
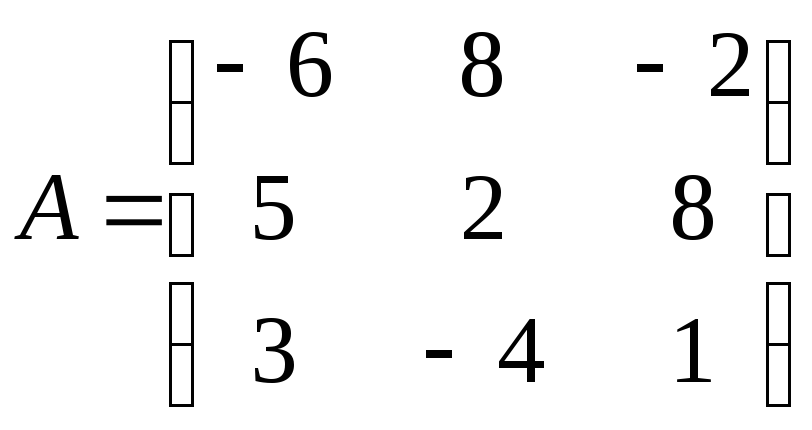
59.
 60.
60.
 .
.
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
-
Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Высш. шк., 1998. – 320 с.
-
Высшая математика для экономистов : практикум / под ред. Н.Ш. Кремера. - 2-е изд., перераб. и доп. - М. : Юнити-Дана, 2007. - 479с.
-
Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. В 2 ч. Ч.1. – М.: Высш. шк., 1996. – 304 с.
-
Клетеник Д.В. Сборник задач по аналитической геометрии. – М.: Наука, 1986. – 224 с.
-
Красс М.С. Математика в экономике. Математические методы и модели: учебник / Красс Максим Семенович, Чупрынов Борис Павлович. - М. : Финансы и статистика, 2007. - 544с.
-
Макаров С.И. Математика для экономистов : учеб. пособие / С. И. Макаров. - 2-е изд., стер. - М. : Кнорус, 2008. - 264с.
-
Шипачев В.С. Курс высшей математики : учебник / Шипачев Виктор Семенович ; под ред. А.Н. Тихонова. - 3-е изд., испр. - М. : Оникс, 2007. - 600с.
Составил: ст.преподаватель кафедры ПИМ Мурзина Н.В.
