Универсальное хеширование

Универсальным хешированием называется хеширование, при котором используется не одна конкретная хеш-функция, а происходит выбор из заданного семейства по случайному алгоритму. Использование универсального хеширования обычно обеспечивает низкое число коллизий. Универсальное хеширование имеет множество применений, например, в реализации хеш-таблиц и криптографии.

Описание

Предположим, что мы хотим отобразить ключи из пространства в числа . На входе алгоритм получает некоторый набор данных и размерностью , причем неизвестный заранее. Как правило целью хеширования является получение наименьшего числа коллизий, чего трудно добиться используя какую-то определенную хеш-функцию.

В качестве решения такой проблемы можно выбирать функцию случайным образом из определенного набора, называемого универсальным семейством .^[6]

Коллизия хеш-функции

Коллизией (иногда конфликтом или столкновением) хеш-функции называются такие два входных блока данных, которые дают одинаковые хеш-коды.

В хеш-таблицах

Большинство первых работ описывающих хеширование было посвящено методам борьбы с коллизиями в хеш-таблицах, так как хеш-функции применялись для поиска в больших файлах. Существует два основных метода используемых в хеш-таблицах:

1. Метод цепочек (метод прямого связывания)

2. Метод открытой адресации

Первый метод заключается в поддержке связных списков, по одному на каждое значение хеш-функции. В списке хранятся ключи, дающие одинаковое значение хеш-кодов. В общем случае, если мы имеем ключей и списков, средний размер хеш-таблицы будет и хеширование приведет к уменьшению среднего количества работы по сравнению с последовательным поиском примерно в раз.

Второй метод состоит в том, что в массиве таблицы хранятся пары ключ-значение. Таким образом мы полностью отказываемся от ссылок и просто просматриваем записи таблицы, пока не найдем нужный ключ или пустую позицию. Последовательность, в которой просматриваются ячейки таблицы называется последовательностью проб.

Криптографическая соль

Существует несколько способов для защиты от подделки паролей и подписей, работающих даже в том случае, если криптоаналитику известны способы построения коллизий для используемой хеш-функции. Одним из таких методов является добавление криптографической соли (строки случайных данных) к входным данным (иногда «соль» добавляется и к хеш-коду), что значительно затрудняет анализ итоговых хеш-таблиц. Данный метод, к примеру, используется для хранения паролей в UNIX-подобных операционных системах.

Применение хеш-функций

Хеш-функции широко используются в криптографии, а также во многих структурах данных — хеш-таблицаx, фильтрах Блума и декартовых деревьях.

Криптографические хеш-функции

Среди множества существующих хеш-функций принято выделять криптографически стойкие, применяемые в криптографии, так как на них накладываются дополнительные требования. Для того чтобы хеш-функция считалась криптографически стойкой, она должна удовлетворять трем основным требованиям, на которых основано большинство применений хеш-функций в криптографии:

• Необратимость: для заданного значения хеш-функции m должно быть вычислительно неосуществимо найти блок данных 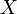, для которого .

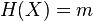• Стойкость к коллизиям первого рода: для заданного сообщения M должно быть вычислительно неосуществимо подобрать другое сообщение N, для которого .

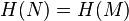• Стойкость к коллизиям второго рода: должно быть вычислительно неосуществимо подобрать пару сообщений 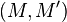, имеющих одинаковый хеш.

Данные требования не являются независимыми:

• Обратимая функция нестойка к коллизиям первого и второго рода.

• Функция, нестойкая к коллизиям первого рода, нестойка к коллизиям второго рода; обратное неверно.

Следует отметить, что не доказано существование необратимых хеш-функций, для которых вычисление какого-либо прообраза заданного значения хеш-функции теоретически невозможно. Обычно нахождение обратного значения является лишь вычислительно сложной задачей.

Атака «дней рождения» позволяет находить коллизии для хеш-функции с длиной значений n битов в среднем за примерно вычислений хеш-функции. Поэтому n-битная хеш-функция считается криптостойкой, если вычислительная сложность нахождения коллизий для неё близка к .

Для криптографических хеш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось (лавинный эффект). В частности, значение хеша не должно давать утечки информации даже об отдельных битах аргумента. Это требование является залогом криптостойкости алгоритмов хеширования, хеширующих пользовательский пароль для получения ключа.

Хеширование часто используется в алгоритмах электронно-цифровой подписи, где шифруется не само сообщение, а его хеш-код, что уменьшает время вычисления, а также повышает криптостойкость. Также в большинстве случаев, вместо паролей хранятся значения их хеш-кодов.