Мультипликативная схема хеширования

Второй метод состоит в выборе некоторой целой константы , взаимно простой с , где  — количество представимых машинным словом значений (в компьютерах IBM PC ). Тогда можем взять хеш-функцию вида:

В этом случае, на компьютере с двоичной системой счисления, является степенью двойки и будет состоять из старших битов правой половины произведения .

Среди преимуществ этих двух методов стоит отметь, что они выгодно используют то, что реальные ключи неслучайны, например в том случае если ключи представляют собойарифметическую прогрессию (допустим последовательность имён «ИМЯ1», «ИМЯ2», «ИМЯ3»). Мультипликативный метод отобразит арифметическую прогрессию в приближенно арифметическую прогрессию различных хеш-значений, что уменьшает количество коллизий по сравнению со случайной ситуацией.

Одной из вариаций данного метода является хеширование Фибоначчи, основанное на свойствах золотого сечения. В качестве здесь выбирается ближайшее к целое число, взаимно простое с 

Хеширование строк переменной длины

Вышеизложенные методы применимы и в том случае, если нам необходимо рассматривать ключи, состоящие из нескольких слов или ключи переменной длины. Например можно скомбинировать слова в одно при помощи сложения по модулю или операции «исключающее или». Одним из алгоритмов, работающих по такому принципу, является хеш-функция Пирсона.

Хеширование Пирсона — алгоритм, предложенный Питером Пирсоном для процессоров с 8-битными регистрами, задачей которого является быстрое вычисление хеш-кода для строки произвольной длины. На вход функция получает слово , состоящее из символов, каждый размером 1 байт, и возвращает значение в диапазоне от 0 до 255. При этом значение хеш-кода зависит от каждого символа входного слова.

Алгоритм можно описать следующим псевдокодом, который получает на вход строку и использует таблицу перестановок :

h := 0

for each c in W loop

index := h xor c

h := T[index]

end loop

return h

Среди преимуществ алгоритма следует отметить:

• простоту вычисления;

• не существует таких входных данных, для которых вероятность коллизии наибольшая;

• возможность модификации в идеальную хеш-функцию.

В качестве альтернативного способа хеширования ключей, состоящих из символов (), можно предложить вычисление

Идеальное хеширование

Идеальной хеш-функцией (англ. Perfect hash function) называется такая функция, которая отображает каждый ключ из набора в множество целых чисел без коллизий. В математических терминах это инъективное отображение.

Описание Функция называется идеальной хеш-функцией для , если она инъективна на ;

1. Функция 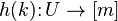называется минимальной идеальной хеш-функцией для 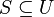, если она является ИХФ и ;

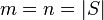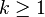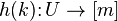2. Для целого , функция называетс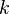я -идеальной хеш-функцией (k-PHF) для 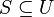если для каждого 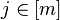имеем .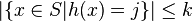

Идеальное хеширование применяется в тех случаях, когда мы хотим присвоить уникальный идентификатор ключу, без сохранения какой-либо информации о ключе. Одним из наиболее очевидных примеров использования идеального (или скорее -идеального) хеширования является ситуация, когда мы располагаем небольшой быстрой памятью, где размещаем значения хешей, связанных с данными хранящимися в большой, но медленной памяти. Причем размер блока можно выбрать таким, что необходимые нам данные, хранящиеся в медленной памяти, будут получены за один запрос. Подобный подход используется, например, в аппаратных маршрутизаторах. Также идеальное хеширование используется для ускорения работы алгоритмов на графах, в тех случаях, когда представление графа не умещается в основной памяти.