Сопромат сборник решенных задач / сопромат / СОПРОМАТ_422 / Расчетная 2
.docРАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА № 2
ОПРЕДЕЛЕНИЕ УСИЛИЙ, НАПРЯЖЕНИЙ И ДЕФОРМАЦИЙ
В ЭЛЕМЕНТАХ, РАБОТАЮЩИХ НА РАСТЯЖЕНИЕ И СЖАТИЕ
ЗАДАЧА № 1
Исходные данные: а=1,0 м, F=26 см2, q1=14 кН/м, q2=18 кН/м, Е=2 105 МПа,
Р1=25 кн, Р2=10 кН
Определить:
1.Определить опорную реакцию в месте закрепления стержня.
2.Вычислить значения продольных сил и нормальных напряжений в характерных сечениях и построить эпюры этих величин.
3.Найти величины абсолютных удлинений (укорочений) участков стержня и величину общего удлинения (укорочения) стержня в целом.
4.Определить значения осевых перемещений характерных сечений и построить эпюру осевых перемещений.
Решение:
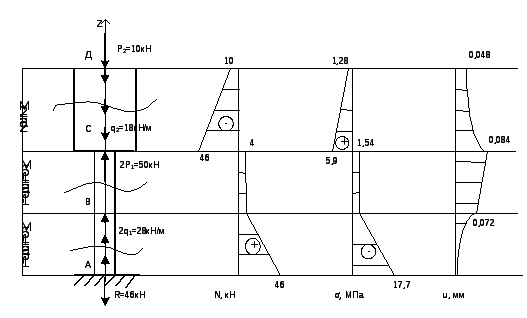
1. Эпюра продольных сил N
Разобьем исходный стержень на 3 участка.
1 участок:
м
z=0
кН,
z=2
кН
2 участок:
м
кН
3 участок:
м
z=0
кН,
z=1,5
кН
По полученным результатам строим эпюру продольных сил.
2. Определим реакцию заделки:
кН
3. Определяем
нормальные напряжения
.
1 участок:
МПа
МПа
2 участок:
МПа
3 участок:
МПа
МПа
По полученным результатам строим эпюру нормальных напряжений.
3.Удлинения (укорочения) участков стержня.
1 участок:
м
мм
2 участок:
м
мм.
3 участок:
м
мм
Общее удлинение стержня:
мм
4. Для построения эпюры осевых перемещений определяем:
мм
мм
мм.
Строим эпюру.
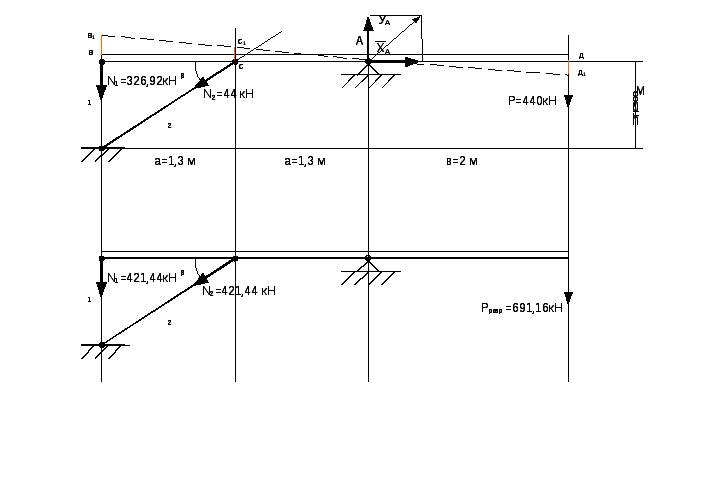
ЗАДАЧА № 2
Исходные данные:
материал стержней сталь марки ВСТ3,
210 МПа , γf
= 1,2,
γс = 0,9, Е=2,1·105 МПа, а=1,3 м, в=1,0 м, h=0,8 м, F2/F1=1, Р=440кН.
Определить:
1.Определить расчетное значение нагрузки.
2.Определить усилия в стержнях системы. Собственную массу элементов стержневой системы не учитывать.
3.Подобрать сечения стрежней в виде двух стальных прокатных равнобоких уголков, используя метод расчета по предельным состояниям.
4.Определить величины нормальных напряжений в поперечных сечениях стержней и проверить выполнение условий прочности.
5.Определить величины удлинений стержней.
6.Определить нагрузку Рт, при которой в системе возникают первые пластические деформации, считая, что материал стержней следует диаграмме Прандтля и имеет предел текучести σт = 240 МПа.
7.Определить разрушающую нагрузку Рразр, при которой система полностью исчерпывает свою несущую способность.
Решение:
1. Для определения усилий в стержнях 1 и 2 воспользуемся уравнением равновесия ΣМА = 0 и уравнением совместности деформаций N1 = k2N2
Составляем уравнение равновесия:
,
Где
Тогда
Составляем дополнительно условие совместности деформаций:
Из чертежа по правилу подобия треугольников получим зависимости
,
где
,
, 
,
где
,
м,
Подставляя значения длин и сокращая на Е, получим
,
т.к значения площадей одинаковое, можем
тоже сократить
Получаем систему уравнений:
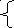
или
Определяем неизвестные:
,
кН,
кН
2. Подбор сечений стержней 1 и 2 производим по формулам:
мм2,
мм2
Так сечение стержней
одинаковое, то выбираем наибольшее
значение площади, учитывая, что сечение
у нас состоит из 2 уголков, значение
площади будет F=791,8мм2=7,91см2,
т.е выбираем
см2
уголок 70х70х6 мм., тогда площадь каждого
стержня будет
см2
3. Проверяем выполнение условий прочности по формулам:
Условие прочности выполняется.
4. Определяем удлинение каждого стержня:
мм
мм
Строим геометрическую схему деформации системы.
ВВ1=
мм,
СС1=
,
,
мм.
(на чертеже пунктирная линия)
5. Определяем предельную грузоподъемность системы. Определяем наиболее нагруженный стержень, это стержень 1, где
Н=391,2кН
Тогда
кН
Подставляем в уравнение равновесия значение N:
кН
При этом значение силы в системе возникают первые пластические деформации.
6. Определяем разрушающую нагрузку Рразр, при которой система полностью исчерпывает свою несущую способность
Для определения разрушающей нагрузки Рразр необходимо рассмотреть предельное состояние системы, при котором в обоих стержнях возникают напряжения, равные пределу текучести σ1 = σт, σ2 = σт и соответствующие усилия N1т = σтF1 , N2т = σтF2
Н=391,2кН
Разрушающая нагрузка определяется из уравнения равновесия системы в предельном состоянии ΣМА = 0.
Подставляем в уравнение равновесия значение N:
кН
Значение разрушающей силы Рразр=642,57 кН.
