
- •Часть 1.
- •Глава 1. Математические основы формализации и методов описания
- •Формализация объекта и парадигмы
- •1.3. Множества и перечень базовых операций над множествами
- •Перечень базовых операций над множествами
- •Области определения функций
- •Обратная функция
- •Теорема
- •Мера и нечеткая мера
- •Задача построения нечетких мер
- •Нечеткие множества: определение и формы записи в операциях и
- •1.7.Функции доверия и правило Демпстера а.Р.,[23]
- •1.8. Нормировка функций в теории нечётких множеств
- •1.9. Нечёткие отношения: прямая и обратная задачи
- •Глава 2. Методы представления знаний с использованием
- •Приближенных и нечетких множеств
Базовые функции. Рассмотрим две одинаковые числовые оси.




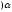






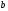
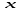
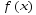
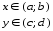
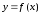 -
числовая функция от х.
-
числовая функция от х.
Если каждому значению х из (a; b) по какому- нибудь закону или правилу f
поставлено в соответствие одно определенное значение другой величины
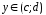 ,
то говорят, что
,
то говорят, что
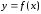 –
естьчисловая
функция от х.
–
естьчисловая
функция от х.
х – аргумент;
(a, b) – область определения функции;
(c,d) – область значений функций.
Например: y = sinx; y = x²;
х – независимая переменная,
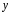
у – зависимая переменная от х.
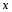

Множество
точек М (х; у), где
 ,
,
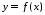 называется
графиком функции
называется
графиком функции
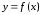 .
.
Простейший вид заданного типа функции называется базовой функцией.
Пример,
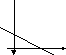
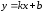 - линейная функция. Базовой функцией
будет являться функция
- линейная функция. Базовой функцией
будет являться функция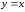 .
.
При построении функции заданного типа предварительно строим график базовой функции.
Пример:
Построить график функции
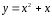 .
.
Перед
нами – квадратичная функция. Ее графиком
является парабола. Базовой функцией
будет являться функция
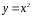 .
.
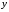

Для построения нашей функции выделим полный квадрат:
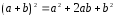
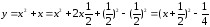
График нашей функции строится в три этапа:
Строим график базовой функции
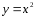
Сдвигаем нашу функцию на
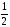 влево:
влево: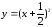
Опускаем график полученной функции на
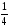 вниз.
вниз.
График
функции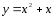
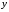

Понятие сложной функции
Для освоения понятия сложной функции введем в рассмотрение промежуточную числовую ось z.
Для
примера рассмотрим функцию
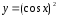 .
Для этой функции, для заданногох,
предварительно вычисляется
.
Для этой функции, для заданногох,
предварительно вычисляется
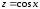 .
Для полученного значенияz
вычисляется
.
Для полученного значенияz
вычисляется
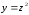 .
Таким образом, в два приема для заданногох,
мы получили значение
.
Таким образом, в два приема для заданногох,
мы получили значение
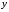 .
Такое задание
.
Такое задание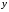 от
х
называется
сложной функцией.
от
х
называется
сложной функцией.


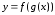 –сложная
функция от х.
–сложная
функция от х.
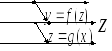
Промежуточных числовых осей может быть несколько.
Например:

Обратная функция



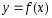
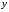
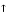
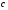



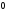
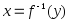
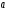
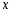
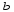
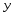
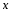
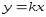

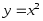

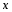
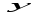
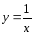
Элементарной функцией будем называть базовую функцию или функцию,
полученную путем четырех арифметических действий из базовых функций, или
взятия сложной функции, последовательно применяемых конечное число раз
 .
.
Говорят,
что функция
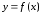 непрерывна
в точке
непрерывна
в точке
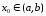 ,
если
выполнены следующие условия:
,
если
выполнены следующие условия:
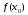 –существует
значение функции в точке
–существует
значение функции в точке

существуют пределы функции слева и справа при

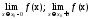
все полученные нами числа должны быть равны между собой.
И записывается это так:
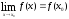
Так
как,
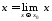 ,то
условие непрерывности примет вид
,то
условие непрерывности примет вид
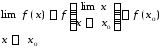

Для непрерывной функции знак предела и знак функции можно переставлять местами.
Разрывная функция





}
скачок
Конечный скачок



Бесконечный скачок
Устранимый
скачок: предел
слева равен пределу справа, а в точке
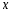
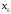 значение
значение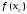 не
существует, или не совпадает с пределами.
не
существует, или не совпадает с пределами.
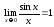

В
точке
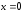 значение функции вычислить нельзя, так
как на 0 делить нельзя.
значение функции вычислить нельзя, так
как на 0 делить нельзя.
Теорема
Всякая элементарная функция непрерывна в области своего определения:
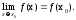
Мера и нечеткая мера
Понятие меры было введено для частных случаев Э. Борелем К. [18], К. Жорданом [19] и А. Лебегом [20]. В современной теории меры Banon G. формулирует его следующим образом, [11].
Пусть
заданы области определения: аддитивный
класс 2x
в
пространстве X
на универсальном множестве X;
значения – множество действительных
чисел R.
Функция множества называется мерой
 ,
если выполняются условия {1,2,3}:
,
если выполняются условия {1,2,3}:
ограниченность -
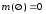 ;
;неотрицательность -
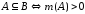 ;
;аддитивность -
 .
.
В теории нечётких множеств используется понятие «нечеткая мера», на основе которой определяется функция доверия.
Пусть теперь заданы области определения, аддитивный класс 2А в пространстве А на универсальном множестве X; значения - отрезок [0,1] на множестве действительных чисел.
Функция множества называется нечеткой мерой g:
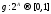 ,
если выполняются условия {1,2,3}:
,
если выполняются условия {1,2,3}:
ограниченность – g (Ø) = 0, g(x)=1;
монотонность – для
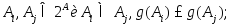
непрерывность – для An
 2A
и
монотонной последовательности
2A
и
монотонной последовательности
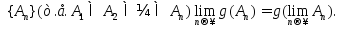
Тройка
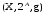 называется
пространством с нечеткой мерой.
называется
пространством с нечеткой мерой.
Задача построения нечетких мер
Пусть
в результате некоторого наблюдения
или эксперимента в
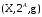 для
для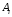 ,
,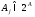 стали
известны (измерены) значения функции
стали
известны (измерены) значения функции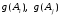 .
.
Задача
построения нечеткой меры заключается
в том, чтобы по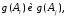 с помощью какого-либо правила, определить
с помощью какого-либо правила, определить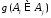 .
.
В
отличие от меры m,
нечеткая мера
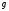 ,
по определению, не является аддитивной,
т.е.
,
по определению, не является аддитивной,
т.е.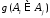 ≠
≠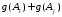 .
.
Поэтому М. Сугэно [21] постулировал λ-правило для построения нечетких мер с параметром нормировки λ:
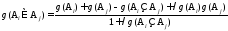
В
частном случае, при
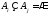 ,λ
-
правило запишем следующим образом:
,λ
-
правило запишем следующим образом:
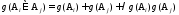
Если
теперь так задать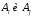 ,
чтобы
,
чтобы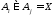 ,
то, с учётом
,
то, с учётом
 ,
получим выражение для параметра
нормировки λ:
,
получим выражение для параметра
нормировки λ:
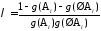 (1.9)
(1.9)
Дальнейшее рассмотрение построения нечетких мер требует их аппроксимации с применением (L-R) функции по Д. Дюбуа и А. Праду [22].
Это может быть выполнено для конкретных нечетких мер из их классификации.
Представим классификацию нечетких мер по Banon G. [11]:

 НЕЧЕТКИЕ
МЕРЫ
НЕЧЕТКИЕ
МЕРЫ

Функция
доверия. Мера необходимости Функция
правдоподобия. Мера возможности

λ>0
λ=0
λ<0
Рис.1.4. Классификация нечетких мер.
Нечеткие множества: определение и формы записи в операциях и
методах представления знаний
Заданы: дискретная область определения – аддитивный класс 2Х в пространстве Х на универсальном множестве Х; область значения – отрезок [0,1] на множестве действительных чисел.
Аксиома
4: функция множества А
называется функцией принадлежности μ,
если для любых
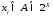 она
отображает область определения на
область значения:
она
отображает область определения на
область значения:
μ:
2X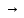 [0,1].
(1.10)
[0,1].
(1.10)
Каждому значению μ(xi) дается одна из следующих понятийных интерпретаций {1,2,3}:
нечеткость суждения
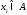 ;
;субъективная совместимость xi и A;
мера нечеткости xi.
Обобщением данных свойств является понятие «нечеткость» (fuzzy) или принадлежность элемента xi множеству A.
Аксиома 5: нечеткое множество НМ есть совокупность упорядоченных пар- элементов множества А и соответствующих им значений функции принадлежности:
{|xi, μ(xi)|}, (1.11)
где
А ={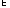 {xi}},
i
{xi}},
i I
I {1,2,…n}.
{1,2,…n}.
Множество А называется носителем нечеткого множества.
На
примере носителя А ={x1,x2,x3}
и значений функций принадлежности
μ(x1)= ,μ(x2)=μ2,
μ(x3)=μ3
приведем основные формы записи нечётких
множеств:
,μ(x2)=μ2,
μ(x3)=μ3
приведем основные формы записи нечётких
множеств:
А = {x1, x2, x3}, (1.12)
μA = μ1, μ2, μ3.
μ1/x1+μ2/x2+μ3/x3=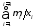 ,
(1.13)
,
(1.13)
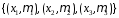 .
(1.14)
.
(1.14)
Каждое нечеткое множество может иметь многоуровневое представление в виде набора носителей, определенных для заданных значений μ:
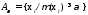 ,
(1.15)
,
(1.15)
где
Аα
–
носитель уровня α,
т.е. подмножество на области определения,
для элементов которого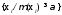 ,i
,i {1,2,..n},
/- связка «при».
{1,2,..n},
/- связка «при».
Например, если для нечетких множеств = {(x1, 0.2), (x2, 0.3), (x3, 0.5)} заданы уровни представления α=0,2 и α=0,3, то получим А0,2 = {x1,x2,x3} и A0,3 ={x2, x3}. Таким образом, данное нечеткое множество на уровнях 0,2 и 0,3 представлено 2-мя носителями: А0,2 = {x1,x2,x3} и A0,3 = {x2,x3}.
К
любому нечеткому множеству, равному
{(xi,
μi)}
с носителем А = {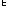 {xi}}
и
{xi}}
и
i I
I {1,2,…n},
можно добавить пару вида (xk,
0), k
{1,2,…n},
можно добавить пару вида (xk,
0), k {1,2,…n}
и k≠i.
{1,2,…n}
и k≠i.
Такая процедура называется модификацией мощности носителя.
Базовые операции над нечеткими множествами с модифицированными носителями: нечеткое множество 1 есть {(xi, μi)} и нечеткое множество 2 равное
{(xi,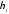 )},i
)},i {1,2,…n},
сводятся к вычислению функции
принадлежности результата {1,2,3,4}:
{1,2,…n},
сводятся к вычислению функции
принадлежности результата {1,2,3,4}:
дополнение
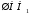 ,
γ=1-μi;
,
γ=1-μi;разность НМ1\НМ2, γ=MIN(μi,1-
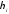 );
);пересечение (произведение)
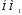 ∩
∩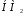 ,
γ=MIN
(μi,
,
γ=MIN
(μi,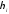 );
);объединение (сумма)
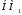
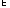
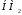 ,
γ=
,
γ=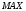 (μi,
(μi, ).
).
1.7.Функции доверия и правило Демпстера а.Р.,[23]
Заданы
области: определения – аддитивный
класс
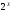 в пространстве
в пространстве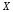 на универсальном множествеX;
значения – отрезок [0;1] на множестве
действительных чисел.
на универсальном множествеX;
значения – отрезок [0;1] на множестве
действительных чисел.
Ограниченность – Bel(ø)=0, Bel(X)=1;
Супераддитивность – для m множеств
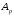
 X.
X.
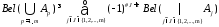 (1.16)
(1.16)
Понятийно Bel – это, по Г. Шеферу (G. Shafer) [24], мера доверия гипотезе, которой соответствует множество в аргументе функции.
Например,
если имеется гипотеза: A
есть одиночное множество {x1}
или {x2},
или {x3},
то A={x1}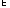 {x2}
{x2}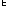 {x3}
и мера доверия этой гипотезе будет равна
Bel(A).
{x3}
и мера доверия этой гипотезе будет равна
Bel(A).
Рассмотрим
частный случай: на множестве
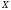 ={x1,x2}
определены
={x1,x2}
определены
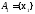 и
и
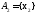 .
Из
супераддитивности функции доверия при
m
=2
следует:
.
Из
супераддитивности функции доверия при
m
=2
следует:
Bel({x1}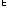 {x2})
{x2}) Bel({x1})+Bel({x2})-({x1}
Bel({x1})+Bel({x2})-({x1}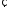 {x2}).
(1.17)
{x2}).
(1.17)
Из ограниченности функции доверия следует:
Bel({x1}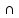 {x2})=Bel(ø)=0,
{x2})=Bel(ø)=0,
Bel({x1}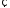 {x2})=Bel(
{x2})=Bel(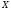 )=1.
(1.18)
)=1.
(1.18)
Используя формулу (1.17), в случае равенства и (1.18), получим:
Bel({x1})+Bel({x2})=1. (1.19)
Из
(1.19), с учётом {x2}= {x1},
вытекает:
{x1},
вытекает:
Bel( {x1})=1-Bel({x1})
. (1.20)
{x1})=1-Bel({x1})
. (1.20)
Соотношение (1.20) называется нормирокой Bel.
Рассмотрим применение нормированной функции доверия для обработки данных.
В
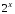 наx={x1,x2,…,xi,…,xn}
определена Bel
и результатом некоторого эксперимента
или наблюдения в
наx={x1,x2,…,xi,…,xn}
определена Bel
и результатом некоторого эксперимента
или наблюдения в
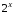 является факт, который известен в виде
элементаxi
и его значения функции принадлежности
μi,
то есть, как нечёткое множество НМ={(xi,
μi)}
с носителем {xi},
является факт, который известен в виде
элементаxi
и его значения функции принадлежности
μi,
то есть, как нечёткое множество НМ={(xi,
μi)}
с носителем {xi},
 принадлежит
{1,2,…,n}.
принадлежит
{1,2,…,n}.
Аксиома 7. Функция доверия с простым носителем:
Bel={0, при A не включаемом в {xi};
μi
при
A,
включенном в {xi};
1- при A=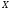 },
где
},
где
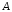 -
множество из гипотез {1,2,3}:
-
множество из гипотез {1,2,3}:
(1.21)
A есть любой элемент {xj}, кроме {xi};
A есть {xi}, или любой другой элемент {xj};
A есть универсальное множество X.
Рассмотрим
теперь простейшую гипотезу: A
есть однозначное множество {xi}.
Дополнительно к свойствам нечёткого
множества, эта гипотеза интерпретируется
как определение меры доверия факту с
помощью соотношения (1.21): Bel
({xi})=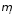 .
.
Пусть теперь все экспериментальные данные сосредоточены на наборе, состоящем из двух фактов:
НМ={(xi,
μi),(xj,
μj)}с
носителем {xi}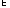 {xj},
{xj},
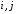 принадлежит{1,2,…,n}.
принадлежит{1,2,…,n}.
Аксиома 8:
Правило
Демпстера: (композиция Bel({xi})
и Bel({xj}))
при их объединении ({xi}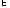 {xj}),
не равна X:
{xj}),
не равна X:
Bel({xi})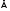 Bel({xj})
=
Bel({xj})
=
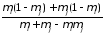 . (1.22)
. (1.22)
Выражение (1.22) определяет меру доверия двум фактам.
Если
все экспериментальные данные сосредоточены
на наборе, состоящем из m
фактов НМ={(xi,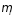 )}
с носителем {
)}
с носителем {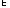 {xi}},
i
{xi}},
i I
I {1,2,…,n},
m=#I,
то получаем композицию:
{1,2,…,n},
m=#I,
то получаем композицию:
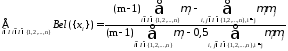 ,
(1.23)
,
(1.23)
Выражение (1.23) определяет меру доверия набору из m фактов.
1.8. Нормировка функций в теории нечётких множеств
В
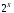 на
на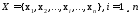 определена и нормирована
определена и нормирована :
:
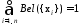 .
(1.24)
.
(1.24)
Опыт системных аналитиков говорит: использование только нормированных функций приводит к тривиальным результатам.
Для устранения тривиальности в теории нечётких множеств изначально заложена ненормированность функции принадлежности:
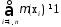 (1.25)
(1.25)
Таким
образом, в нечётких технологиях
используется ненормированная входная
функция
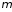 ,
а внутренние (например,Bel)
и выходные – нормированы.
,
а внутренние (например,Bel)
и выходные – нормированы.
Это позволяет учитывать все особенности и противоречия внешнего (физического) мира, а на выходе из технологии (дефаззификация) получать результаты в привычном диапазоне, например от 0 до 1, или в процентах.
1.9. Нечёткие отношения: прямая и обратная задачи
В
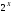 на
на определены
нечёткие множества.
определены
нечёткие множества.
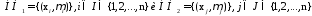 ,
(1.26)
,
(1.26)
Аксиома 9:
Нечёткие
отношения (НО) двух нечётких множеств
есть совокупность упорядоченных пар
{xi,
xj}
и соответствующих им значений функции
принадлежности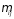 :
:
 .
(1.27)
.
(1.27)
Нечёткое отношение между НМ1 и НМ2 есть частный случай использования композиционных правил нечёткого ввода НМ1 => НМ2.
Пусть
имеется два набора факторов НМ1=
{(xi,
μi)},
где i
равно от 1
до n,
НМ2=
{xj,
μj},
где j
равно от 1
до n
и установлена зависимость между ними
в виде правила: НМ1
=> НМ2,
которому соответствует нечёткое
отношение {(xi,xj),
(μi,
μj)}.
Теперь, если известен набор фактов НМ1’=
{xi’,
μi’},
где i
принадлежит от 1 до n,
то можно сделать нечёткий вывод, что
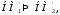 или
по
или
по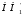 определить
определить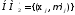 ,
используя правило композиции:
,
используя правило композиции:
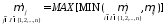 (1.28)
(1.28)
перебором
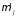 ,
или методом С.Ю. Маслова, [25]. Приближённое
решение
,
или методом С.Ю. Маслова, [25]. Приближённое
решение
(в сторону уменьшения Bel):
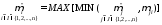 ,
(1.29)
,
(1.29)
где μji - матрица транспонирования относительно μij.
Глава 2. Методы представления знаний с использованием
Приближенных и нечетких множеств
