Практическая работа № 4 по основам медико-биологической статистики.
Задание 1. Выучить, описать словами порядок действий, задаваемый формулами.
Техника построения вариационного ряда.
Собирают исходные данные для статистического анализа.
Далее призводится группировка исходных данных в статистические ряды – ряды числовых значений признака, расположенных в определённом порядке.
Статистические ряд:
1) атрибутивный;
(число людей с группой крови)
2) вариационный (или ряд распределения);
Двойной
ряд чисел, показывающий, каким образом
числовые значения признака ( )
связаны с их повторяемостью (
)
связаны с их повторяемостью ( – частота или вес (веса) вариант(а),
– частота или вес (веса) вариант(а), Относительные частоты или частости).
Относительные частоты или частости).
3) временной.
Находят:
1.
 ;
;
2.
По формуле Старджеса (1926): К =
 ,(15-20)!
,(15-20)!
3. величина
классового интервала
 ,
,
а) Если значения признак выражены целыми числами и классовый интервал окажется равным единице или может быть приравнён (приравнен) к единице, выборка распределяется в безынтервальный вариационный ряд.
б)
 ,
выборку следует распределять в
интервальный вариационный ряд
,
выборку следует распределять в
интервальный вариационный ряд ,
,
 ,
если
,
если
При построении
классового интервала следует добиваться
того, чтобы минимальная варианта
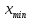 попадала в середину первого классового
интервала.
попадала в середину первого классового
интервала. ,
где
,
где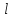 – нижняя граница первого классового
интервала.
– нижняя граница первого классового
интервала.
Разнести варианты по классам. Допустимо в один и тот же класс помещать варианты, которые больше нижней, но меньше или равны его верхней границе.
Средние величины, показатели вариации вычисляются на безынтервальных рядах, то интервальный ряд приходится превращать в ряд безынтервальный. Это достигается заменой классовых интервалов центральными или срединными значениями они определяются по полу сумме нижних границ предыдущего и последующего классов.
Медиана (Ме). Значение относительно которого ряд распределения делится на две половины. Число членов ряда нечётное, то (Ме) — центральная варианта. Чётное число членов ряда — (Ме) (полусумма) полу сумма двух соседних вариант в центре ряда.
Если выборка распределена в интервальный вариационный ряд, то:
1.
находят класс или интервал, где находится
медиана. Кумулируют частоты ряда в
направлении от меньших к большим до
величины
 превосходящей
превосходящей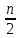 .
.
 — нижняя граница медианного интервала.
— нижняя граница медианного интервала.
 (1)
(1)
Мода (Мо) — величина , которая встречается в данной совокупности наиболее часто.
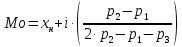 ,
(2)
,
(2)
где
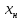 —
нижняя граница модального класса, т.е.
класса с наибольшей частотой
—
нижняя граница модального класса, т.е.
класса с наибольшей частотой ;
;
 частота класса, предшествующего
модальному;
частота класса, предшествующего
модальному; — частота класса, следующего за модальным;
— частота класса, следующего за модальным;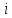 — величина классового интервала
— величина классового интервала
Квантили – отсекают в пределах ряда определённую часть его членов.
Квартиль
— величина, отсекающая
 членов ряда. Три квартиля делят ряд на
четыре равночисленные части (кварты).
членов ряда. Три квартиля делят ряд на
четыре равночисленные части (кварты).
Дециль
— величина, определяющая
 всех
члены ряда. Девять децилей делят рядна
десять равных частей.
всех
члены ряда. Девять децилей делят рядна
десять равных частей.
Сотые
доли числа вариант —
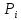 называетсяперцентилемилипроцентилем.
называетсяперцентилемилипроцентилем.
99 Перцентилей делят всю совокупность наблюдений на 100 равночисленных частей.
Любой перцентиль определяется рядом последовательных действий, которые модно выразить в виде следующей формулы:
 (3)
(3)
 —
нижняя граница класса, содержащего
перцентиль
—
нижняя граница класса, содержащего
перцентиль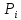 ;
она определяется по величине
;
она определяется по величине
 ,
превосходящей (или равной) числу
,
превосходящей (или равной) числу в ряду накопленных частот.
в ряду накопленных частот.
Здесь
 — выбранный перцентиль;
— выбранный перцентиль; частота класса, содержащего перцентиль
частота класса, содержащего перцентиль ;
;
 — величина классового интервала;
— величина классового интервала;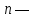 общее число наблюдений, или объём
выборки.
общее число наблюдений, или объём
выборки.
Формула (3) применима и в случаях, когда выборочная совокупность распределяется в безынтервальный вариационный ряд, т.е. непосредственно по ранжированным значениям признака.
Значение квантилей.
1. Квантили, медиана – ценные характеристики варьирующих объектов, особенно при резко выраженных асимметрии в распределении частот по классам вариационного ряда.
2. Независимо от закона распределения квантили используются
1.как структурные средние;
2.как показатели вариации;
3. используются для установления границ тех или иных нормативов (при оценке физического развития человека, спортивных достижений отдельных индивидов
Задание 2.
Разобрать два примера.
Пример 1. Данные, полученные в конце 60-ч годов в СССР при исследовании ритмов сердечных сокращений у 861-ого спортсмена (в покое), количественно охарактеризовали длительность TP-сегмента ЭКГ, Результаты исследования сведены в таблицу №1.
|
х,
|
30- |
35- |
40- |
45- |
50- |
55- |
60- |
65- |
70- |
75- |
80- |
85- |
90-95 |
|
|
8 |
20 |
41 |
54 |
50 |
101 |
61 |
152 |
150 |
123 |
74 |
24 |
3 |
|
|
8 |
28 |
69 |
123 |
173 |
274 |
335 |
487 |
637 |
760 |
834 |
858 |
861 |
В таблице №1:
х,
 с
- длительностьTP-сегмента
ЭКГ;
с
- длительностьTP-сегмента
ЭКГ;
 - число случаев («частоты»);
- число случаев («частоты»);
 -
«накопленные частоты», кумулированное
число случаев от меньших к большим
значениям классов.
-
«накопленные частоты», кумулированное
число случаев от меньших к большим
значениям классов.
Найдите, используя, представленные в таблице №1 данные, 50-й процентиль (перцентиль) сердечных сокращений у спортсменов по показателям длительности TP-сегментов ЭКГ.
Решение:
Определим

Величина
К находится между
 =
335 и
=
335 и =
487. Нижняя граница этого интервала,
содержащего перцентиль
=
487. Нижняя граница этого интервала,
содержащего перцентиль ,
равна 65.
,
равна 65.
Берём
разность
 =430,5
– 335 = 95,5 и относим её к частоте класса,
содержащего искомый перцентиль, т.е. к
частоте
=430,5
– 335 = 95,5 и относим её к частоте класса,
содержащего искомый перцентиль, т.е. к
частоте
Учитывая
величину классового интервала
 ,
подставляем известные значения в
формулу:
,
подставляем известные значения в
формулу:

 .
.
Эта величина соответствует медиане данного распределения.
Она оказалась несколько больше средней арифметической, равной 65,87.
Если
принять за норму сердечных сокращений
у спортсменов величину, равную 50% всех
членов ряда, то её границы определятся
по
 и
и .
.
Найдём эти границы.
Сначала
вычислим
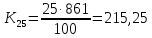 и
и .
.
Отсюда
 и
и

Пример 2. Измерены длинны = 100 иголок на ветви ели в миллиметрах.
По этим данным определена средняя длина
иголок (хвоинок)
= 100 иголок на ветви ели в миллиметрах.
По этим данным определена средняя длина
иголок (хвоинок) и их отклонения от среднего значения
и их отклонения от среднего значения .
Минимальное и максимальное отклонения
составили соответственно -2,5 и 5,0. В
соответствии с формулой Старджеса
(1926){
.
Минимальное и максимальное отклонения
составили соответственно -2,5 и 5,0. В
соответствии с формулой Старджеса
(1926){ }
диапазон отклонений разбит на
}
диапазон отклонений разбит на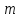 = 8 ){
= 8 ){ }
равных интервалов и подсчитано количество
наблюдений, попавших в каждый интервал.
Данные представлены (сведены в) в таблице:
}
равных интервалов и подсчитано количество
наблюдений, попавших в каждый интервал.
Данные представлены (сведены в) в таблице:
|
Границы интервалов |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
|
3 |
10 |
15 |
24 |
25 |
13 |
7 |
3 |
Требуется при уровне значимости α = 0,01 проверить гипотезу о том, что отклонения длины иголочки ели от среднего значения согласуются с нормальным законом распределения.
Решение: Поскольку число наблюдений в крайних интервалах мало, объединим крайние интервалы с соседними.
В результате объединения получим таблицу:
|
Границы интервалов |
-3 |
-1 |
0 |
1 |
2 |
3 |
|
|
13 |
15 |
24 |
25 |
13 |
10 |
Для
получения теоретических вероятностей
 попадания случайных отклоненийXв соответствующие интервалы необходимо
знать параметры предполагаемого
нормального распределения: математическое
ожидание и дисперсию.
попадания случайных отклоненийXв соответствующие интервалы необходимо
знать параметры предполагаемого
нормального распределения: математическое
ожидание и дисперсию.
Оценки параметров генеральной совокупности сделаем по выборке (сведена в таблицу), воспользовавшись формулами:



где
 — середины соответствующих интервалов.
В формулах предполагается Что интервалы
имеют одинаковую длину, поэтому следует
воспользоваться первоначальной таблицей.
Расчёты дают:
— середины соответствующих интервалов.
В формулах предполагается Что интервалы
имеют одинаковую длину, поэтому следует
воспользоваться первоначальной таблицей.
Расчёты дают: ;
; ;
; 1,6.
1,6.
Произведём
вычисления вероятностей
 .
.
Для первого интервала:


 .
.
По таблице интеграла вероятностей(и) находим:

 ,
,
Отсюда
 .
.
Аналогично:
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
Границы интервалов |
-3 |
-1 |
0 |
1 |
2 |
3 |
|
|
13 |
15 |
24 |
25 |
13 |
10 |
|
|
|
|
|
|
|
|
|
|
|
0,1933 |
0,2467 |
0,2119 |
0,1296 |
0,06338 |
Вычислим
величину
 :
:
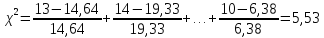 .
.
Число
интервалов равно 6. По выборке оценивались
два параметра, следовательно, число
степеней свободы l=6-1-2=3.
По таблице распределения находим
находим
 .
.
Поскольку
 ,
то нет оснований отвергать проверяемую
гипотезу.
,
то нет оснований отвергать проверяемую
гипотезу.
Задание 3. Провести самостоятельное статистическое исследование:
«Статистическое исследование длины хвоинки с ветки Picea abies ели обыкновенной»
«Проверка статистической гипотезы о том, что распределение в генеральной совокупности является нормальным (гауссовым законом распределения)»
Формулировка задачи исследования. Жизненный опыт говорит о том, что окружающие нас люди, животные и растения характеризуются некоторым разнообразием однородных признаков. Различные антропометрические данные, существование различных размеров обуви, головных уборов, одежды, перчаток и т.п. являются проявлением общей биологической закономерности. Наследуется не признак, а норма реакции. Есть все основания предполагать, что количественная характеристика признака (рост, масса) в однородной популяции должна содержать некоторое среднее значение и меру разброса около этого среднего.
Для нашего статистического исследования выберем веточку ёлки (Picea abies) и будем измерять длину иголок с этой ветки. В силу действия разнонаправленных, хаотически меняющихся факторов, которые могут повлиять на длину иголки, выглядят логичными предположение о том, что длина распределена на ветке ели по нормальному закону.

 с
с
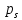
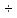 -2
-2 -1
-1 0
0 1
1 2
2 3
3 4
4 5
5
 -1
-1 0
0 1
1 2
2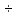 3
3 5
5
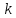
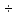 -1
-1 0
0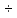 1
1 2
2 3
3 5
5