КЛА ЭКЗик / 3лек

1. Определение минимальной величины импульса перелета (принцип Хомана.)

Рассмотрим перелет КЛА с исходной орбиты высотой на конечную орбиту, высотой , при этом затратив минимум энергии.

Подобная задача решена Хоманом. Рассмотрим перелет с одной круговой орбиты на другую круговую орбиту. ( рис.1 )

Обозначим индексом 1- параметры, относящиеся к исходной орбите,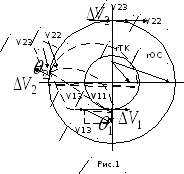

индексом – 2, параметры конечной орбиты, индексом – 3, параметры орбиты перелета.

В точке схода, обозначенной – 1, прикладываем под углом 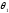импульс схода с опорной орбиты - .

При этом аппарат получит скорость

где 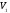- скорость в точке схода на опорной орбите,

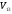- скорость в точке схода на орбите перелета,

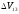- импульс перелета в точке 1,

- угол наклона скорости схода в точке схода.

По достижении высоты конечной орбиты аппарат должен перейти на эту орбиту, для чего необходимо сообщить ему импульс 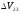для перехода на конечную орбиту.

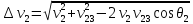
где 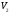- скорость полета по конечной орбите,

- скорость полета по орбите перелета в точке 2,

- импульс перехода с орбиты перелета на рабочую орбиту;

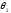- угол наклона скорости в точке 2 орбиты перелета.

Суммарный импульс на маневрирование равен

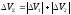1- 4

Независимой переменной, от величины, которой зависит импульс перелета, будет угол приложения импульса. Продифференцируем выражения ( 1-1 и 1-2) соответственно по углам: 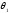и 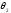и прировняв к нулю получим значения углов, соответствующие экстремальным значениям импульсов.

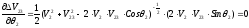
Производные могут быть равны нулю только в случае если

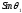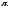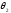=0, что возможно, если = 0 или равен _, соответственно если =0 или равен 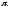Это возможно только в том случае если импульс приложен по касательной к траектории.

Отсюда следует, что для получения минимального импульса, необходимого для перелета с одной круговой орбиты на другую круговую орбиту необходимо приложить импульс по касательной к орбите.

В этом случае импульс, потребный для схода с орбиты (1) равен

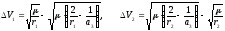
Найдем угловое расстояние, которое в этом случае пролетит аппарат. Имеем выражение для угла наклона скорости к горизонту:

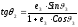
где 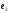- эксцентриситет орбиты перелета,

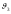- истинная аномалия точки схода с опорной орбиты.

В случае приложения импульса по касательной угол 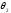=0, что возможно, если 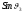=0, а это возможно, при =, где .

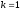Таким образом, для получения минимального импульса, потребного на перелет КЛА с одной круговой орбиты на другую, импульс перехода должен быть приложен по касательной, как в точке схода, так и в точке прилета. Угловое расстояние, которое в этом случае пролетит аппарат равно 180 градусам.

Время перелета равно половине периода обращения по орбите перелета.

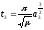
где - время полета с момента сход до прилета на конечную орбиту,

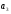- большая полуось орбиты перелета.

Время перелета , в этом случае, не будет минимальным.

Найдем условие, при котором будем иметь минимальное время перелета. Время перелета между двумя точками эллиптической орбиты равно

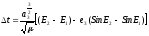1- 5

где Е – эксцентрическая аномалия.

Если считать точку схода с опорной орбиты за начало отсчета, то формула примет вид

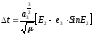1-6

где - эксцентрическая аномалия точки прилета, равная

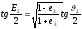
Для нахождения условия минимальности дифференцируем выражение по 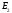и приравняем нулю.

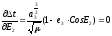
что возможно если

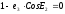
откуда

1- 7

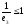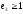Поскольку косинус не может быть больше 1, то выражение , следовательно , что соответствует гиперболическим траекториям, чем больше будет величина эксцентриситета, тем меньше время перелета.

Скорость, потребная для осуществления этого маневра равна

,

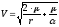а импульс, потребный на перелет

.,