КЛА ЭКЗик / 4лек

Объемный маневр.

Для запуска геостационарных спутников связи и построения различных космических систем требуется выводить КА в плоскость с определенным углом наклона, что не всегда возможно из-за расположения космодрома. Эти задачи решаются с помощью маневра, получившего название «Объемного маневра», маневра заключающегося в повороте плоскости орбиты КА, или изменению угла – i.

Возможны два способа поворота плоскости отбиты.

1. Совместить изменение угла наклонения плоскости орбиты и изменение положения восходящего и нисходящего узлов орбиты. Импульс прикладывается в определенной точке орбиты.

2. Изменение только угла наклонения орбиты, импульс прикладывается в одном из узлов орбиты.

А) Изменение угла наклона плоскости орбиты при приложении импульса поворота в произвольной точке орбиты.

Для изменения угла наклонения плоскости орбиты, импульс скорости поворачивающий плоскость орбиты необходимо приложит в плоскости перпендикулярной плоскости орбиты. На рис. 2 видно, что бинормальный импульс 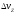повернет вектор скорости

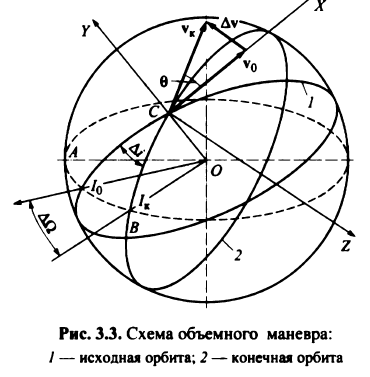
КА, а вместе с ней и плоскость исходной орбиты на угол ,

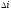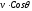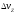В выражении − горизонтальная составляющая скорости КА. Знак минус обозначает, что положительный импульс скорости поворачивает плоскость исходной орбиты на отрицательный угол 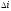. Горизонтальная составляющая скорости равна

Тогда угол поворота плоскости исходной орбиты, при известных значениях параметров

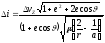
Положение плоскости орбиты в иене инерциальном пространстве определяется углами: − угол восходящего узла орбиты и i – угол наклона плоскости орбиты к горизонту. Изменение угла наклонения орбиты i приводит к изменению угла 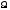и аргумента широты перигея .Связь между этими углами можно найти, если рассмотреть сферический треугольник АВС. Дуга АС = , дуга ВС = 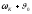, Наклонение орбиты после выполнения маневра можно вычислить из выражения

Б) Изменение угла наклонения плоскости орбиты, при подаче импульса в узле орбиты.

Импульсный поворот, в этом случае в одном из узлов орбиты прикладывается импульс скорости, с помощью которого поворачивается скорость КА, и он переходит в другую плоскость, не осуществляя перелета.

На рис.2 приведена схема решения задачи разворота. В восходящем узле орбиты приложен импульс скорости – 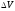, под действием этого импульса скорость КА, равная 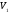поворачивается на угол – 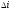. Величина скорости может изменяться или оставаться постоянной.

Величина импульса скорости, потребного на поворот плоскости орбиты на угол – 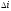при изменении скорости полета КА находится из выражения

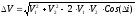
где 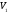- скорость полета по исходной орбите,

- скорость полета по орбите, после ее поворота,

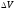- импульс, потребный на поворот плоскости орбиты,

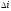- угол поворота плоскости орбиты.

Если 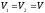, то

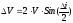
Если угол поворота мал, то косинус можно разложить в ряд

тогда

,

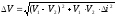если 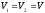, тогда