
- •ЛЕКЦИЯ 1
- •2. Электричество и магнетизм
- •2.1. Электростатика
- •2.1.1. Электрический заряд. Закон сохранения заряда
- •2.1.2. Взаимодействие электрических зарядов в вакууме. Закон Кулона
- •2.1.3. Электростатическое поле. Напряженность электростатического поля
- •2.1.4. Сложение электростатических полей. Принцип суперпозиции
- •2.1.5. Электростатическое поле диполя
- •2.1.6. Взаимодействие двух диполей
- •ЛЕКЦИЯ 2
- •2.1.7. Силовые линии электростатического поля
- •2.1.8. Поток вектора напряженности
- •2.1.9. Теорема Остроградского-Гаусса
- •ЛЕКЦИЯ 3
- •2.1.11. Теорема о циркуляции вектора поля
- •2.1.12. Работа сил электростатического поля. Потенциальная энергия
- •ЛЕКЦИЯ 4
- •2.1.13. Связь между напряженностью и потенциалом
- •2.1.14. Безвихревой характер электростатического поля
- •2.1.15. Силовые линии и эквипотенциальные поверхности
- •2.1.16. Расчет потенциалов простейших электростатических полей
- •ЛЕКЦИЯ 5
- •2.1.17. Поляризация диэлектриков
- •2.1.18. Различные виды диэлектриков
- •2.1.19. Вектор электрического смещения
- •ЛЕКЦИЯ 6
- •2.1.21. Изменение D и E на границе раздела двух диэлектриков
- •2.1.22. Напряженность и потенциал электростатического поля в проводнике
- •2.1.23. Определение напряженности поля вблизи поверхности заряженного проводника
- •2.1.24. Конденсаторы
- •ЛЕКЦИЯ 7
- •2.1.25. Энергия электростатического поля
- •2.1.26. Причины электрического тока
- •2.1.27. Плотность тока
- •2.1.28. Уравнение непрерывности
- •2.1.29. Сторонние силы и ЭДС
- •ЛЕКЦИЯ 8
- •2.1.30. Закон Ома для неоднородного участка цепи
- •2.1.31. Закон Ома в дифференциальной форме
- •2.1.32. Работа и мощность тока. Закон Джоуля – Ленца
- •2.1.33. КПД источника тока
- •ЛЕКЦИЯ 9
- •2.2. Электромагнетизм
- •2.2.1. Магнитные взаимодействия
- •2.2.2. 3акон Био–Савара–Лапласа
- •ЛЕКЦИЯ 10
- •2.2.3. Магнитное поле движущегося заряда
- •2.2.4. Напряженность магнитного поля
- •2.2.5. Магнитное поле прямого тока
- •2.2.6. Магнитное поле кругового тока
- •ЛЕКЦИЯ 11
- •2.2.7. Теорема Гаусса для вектора магнитной индукции
- •2.2.8. Закон Ампера
- •2.2.9. Взаимодействие двух параллельных проводников с током
- •ЛЕКЦИЯ 12
- •2.2.10. Воздействие магнитного поля на рамку с током
- •2.2.11. Сила Лоренца
- •2.2.12. Циркуляция вектора магнитной индукции
- •ЛЕКЦИЯ 13
- •2.2.13. Магнитное поле соленоида
- •2.2.14. Магнитное поле тороида
- •2.2.15. Работа по перемещению проводника с током в магнитном поле
- •ЛЕКЦИЯ 14
- •2.2.16. Опыты Фарадея. Индукционный ток. Правило Ленца
- •2.2.17. Величина ЭДС индукции
- •2.2.18. Природа ЭДС индукции
- •ЛЕКЦИЯ 15
- •2.2.19. Циркуляция вектора напряженности вихревого электрического поля
- •2.2.20. Явление самоиндукции
- •2.2.21. Влияние самоиндукции на ток при замыкании и размыкании цепи, содержащей индуктивность
- •ЛЕКЦИЯ 16
- •2.2.22. Взаимная индукция
- •2.2.23. Индуктивность трансформатора
- •2.2.24. Энергия магнитного поля
- •2.2.25. Магнитное поле в веществе
- •ЛЕКЦИЯ 17
- •2.2.26. Диамагнетики и парамагнетики в магнитном поле
- •2.2.27. Ферромагнетики
- •2.2.28. Закон полного тока
- •ЛЕКЦИЯ 18
- •2.2.29. Ток смещения
- •2.2.30. Единая теория электрических и магнитных явлений. Система уравнений Максвелла
- •ЛЕКЦИЯ 19
- •2.3. Колебания и волны
- •2.3.1. Виды и признаки колебаний
- •2.3.2. Параметры гармонических колебаний
- •2.3.3. Графики смещения скорости и ускорения
- •2.3.4. Основное уравнение динамики гармонических колебаний
- •ЛЕКЦИЯ 20
- •2.3.5. Энергия гармонических колебаний
- •2.3.6. Математический и пружинный маятник
- •2.3.7. Гармонический осциллятор
- •2.3.8. Сложение гармонических колебаний одного направления и одинаковой частоты. Биения
- •ЛЕКЦИЯ 21
- •2.3.9. Сложение взаимно перпендикулярных колебаний
- •2.3.10. Фигуры Лиссажу
- •2.3.11. Свободные затухающие механические колебания
- •2.3.12. Коэффициент затухания и логарифмический декремент затухания
- •ЛЕКЦИЯ 22
- •2.3.13. Вынужденные механические колебания
- •2.3.14. Свободные колебания в электрическом контуре без активного сопротивления
- •2.3.15. Свободные затухающие электрические колебания
- •ЛЕКЦИЯ 23
- •2.3.16. Вынужденные электрические колебания
- •2.3.17. Мощность, выделяемая в цепи переменного тока
- •2.3.18. Распространение волн в упругой среде
- •ЛЕКЦИЯ 24
- •2.3.19. Уравнения плоской и сферической волн
- •2.3.20. Фазовая скорость
- •2.3.21. Принцип суперпозиции. Групповая скорость
- •2.3.22. Стоячие волны
- •ЛЕКЦИЯ 25
- •2.3.23. Волновое уравнение
- •2.3.24. Дифференциальное уравнение электромагнитных волн
- •2.3.25. Энергия и импульс электромагнитного поля. Плотность потока энергии. Вектор Умова-Пойтинга
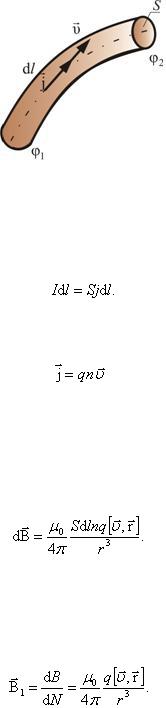
ЛЕКЦИЯ 10
2.2.3. Магнитное поле движущегося заряда
Как известно, электрический ток – упорядоченное движение зарядов, а, как мы доказали только что, магнитное поле порождается движущимися зарядами. Найдем магнитное поле, создаваемое одним движущимся зарядом (рис. 2.2.5).
Рис. 2.2.5
В уравнении (2.2.4) заменим ток I на jS, где j – плотность тока. Векторы j и dl имеют одинаковое направление, значит
Если все заряды одинаковы и имеют заряд q, то
, |
(2.2.7) |
где n – число носителей заряда в единице объема;  – дрейфовая скорость зарядов.
– дрейфовая скорость зарядов.
Если заряды положительные, то j и  имеют одно направление (рис. 2.2.4). Подставив (2.2.7) в (2.2.4), получим:
имеют одно направление (рис. 2.2.4). Подставив (2.2.7) в (2.2.4), получим:
(2.2.8)
,
Обозначим  – число носителей заряда в отрезке dl . Разделив (2.2.8) на это число, получим выражение для индукции магнитного поля, создаваемого одним зарядом, движущимся со скоростью
– число носителей заряда в отрезке dl . Разделив (2.2.8) на это число, получим выражение для индукции магнитного поля, создаваемого одним зарядом, движущимся со скоростью  :
:
(2.2.9)
,
В скалярной форме индукция магнитного поля одного заряда в вакууме определяется по формуле:
92

(2.2.10)
,
Эта формула справедлива при скоростях заряженных частиц  .
.
2.2.4. Напряженность магнитного поля
Итак, мы с вами выяснили, что магнитное поле – это одна из форм проявления электромагнитного поля, особенностью которого является то, что это поле действует
только на движущиеся частицы и тела, обладающие электрическим зарядом, а также на намагниченные тела.
Магнитное поле создается проводниками с током, движущимися электрическими заряженными частицами и телами, а также переменными электрическими полями.
Силовой характеристикой магнитного поля служит вектор магнитной индукции B поля созданного одним зарядом в вакууме:
 .
.
Еще одной характеристикой магнитного поля является напряженность.
Напряженностью магнитного поля называют векторную величину H ,
характеризующую магнитное поле и определяемую следующим образом:
(2.2.11)
,
Напряженность магнитного поля заряда q, движущегося в вакууме равна:
(2.2.12)
,
Это выражение показывает закон Био–Савара–Лапласа для H .
Напряженность магнитного поля H является, как бы, аналогом вектора электрического смещения D в электростатике.
2.2.5. Магнитное поле прямого тока
Применим закон Био–Савара–Лапласа для расчета магнитных полей простейших токов.
Рассмотрим магнитное поле прямого тока (рис. 2.2.6).
93
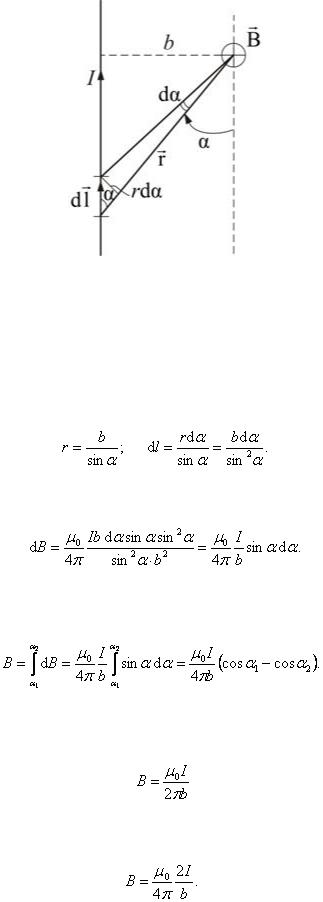
Рис. 2.2.6
Все векторы dB от произвольных элементарных участков dl имеют одинаковое направление. Поэтому сложение векторов можно заменить сложением модулей.
Пусть точка, в которой определяется магнитное поле, находится на расстоянии b от провода. Из рисунка 2.2.6 видно, что:
Подставив найденные значения r и dl в закон Био–Савара–Лапласа, получим:
Для конечного проводника угол α изменяется от  , до
, до  . Тогда
. Тогда
(2.2.13)
,
Для бесконечно длинного проводника  а
а  , тогда
, тогда
или, что удобнее для расчетов,
(2.2.2)
,
Линии магнитной индукции прямого тока представляют собой систему концентрических окружностей, охватывающих ток (рис. 2.2.3).
94
2.2.6. Магнитное поле кругового тока
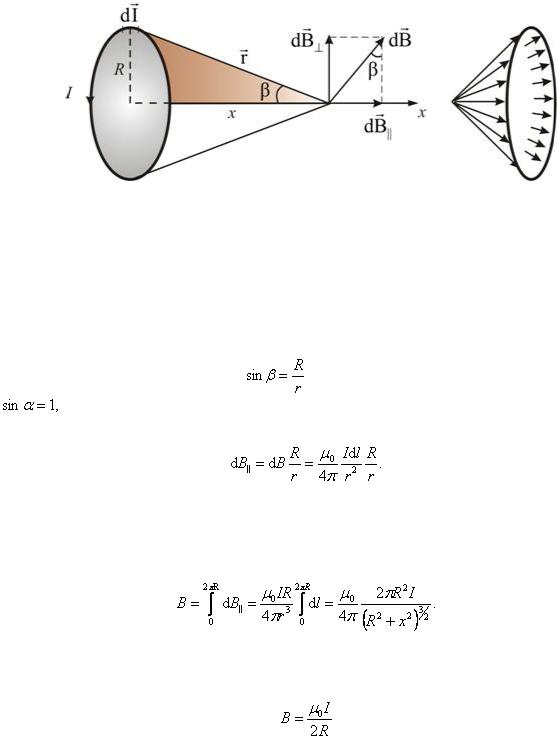
Рассмотрим поле, создаваемое током I, текущим по тонкому проводу, имеющему форму окружности радиуса R (рис. 2.2.7).
Рис. 2.2.7
Определим магнитную индукцию на оси проводника с током на расстоянии х от плоскости кругового тока. Векторы dB перпендикулярны плоскостям, проходящим через соответствующие dl и r . Следовательно, они образуют симметричный конический веер. Из соображения симметрии видно, что результирующий вектор B направлен вдоль оси кругового тока. Каждый из векторов dB вносит вклад равный  , а
, а  взаимно
взаимно
уничтожаются. Но  , , а т.к. угол между dl и r α – прямой, то
, , а т.к. угол между dl и r α – прямой, то
тогда получим |
|
, |
(2.2.14) |
|
Подставив в (2.2.14)  и, проинтегрировав по всему контуру
и, проинтегрировав по всему контуру  ,
,
получим выражение для нахождения магнитной индукции кругового тока:
(2.2.15)
,
При  , получим магнитную индукцию в центре кругового тока:
, получим магнитную индукцию в центре кругового тока:
(2.2.16)
,
95
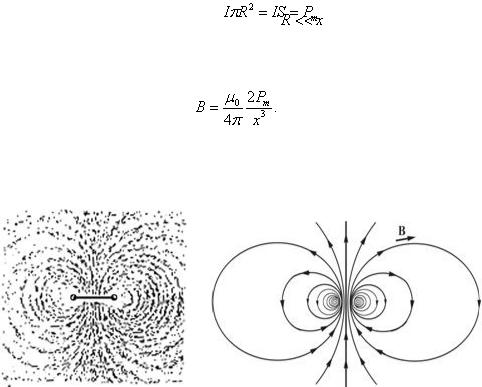
Заметим, что в числителе (2.2.15) |
|
– магнитный момент контура. |
Тогда, на большом расстоянии от контура, при |
|
, магнитную индукцию можно |
рассчитать по формуле: |
|
|
|
, |
(2.2.17) |
|
|
Силовые линии магнитного поля кругового тока хорошо видны в опыте с железными опилками (рис. 2.2.8).
Рис. 2.2.8
96
